Сферические волны передающих линейных магнитных антенн (Часть II)

1. Настоящая работа  посвящена возможности использования передающих линейных магнитных антенн (ЛМА) для  электромагнитной цифровой связи  в ОНЧ и КНЧ диапазоне между мобильными погруженными в морскую среду объектами и  об особенности работы Передающей Линейной Ферритовой Антенны (ПЛФА) типа ЛМА [1, 2, 3].

Типичными  представителями ПЛФА являются модели Передающих Линейных Магнитных Антенн ПЛМА, изложены в Описаниях Патентов  [1, 2] и статье [3]: "Сферические волны передающих Линейных Магнитных Антенн(часть I)" автора настоящей работы.

Ознакомиться с некоторыми моделями ПЛМА, материалами лабораторных испытаний и используемыми измерительными приборами  можно на сайте www.lret.ru.

В настоящей работе автор в отличие от статьи [3], где рассматривалась теория работы ПЛМА в свободном пространстве (в вакууме), иллюстрирует теоретические основы применения  ПЛМА в поглощающих и проводящих средах.

ПЛМА - как  излучатели электромагнитных волн типа Магнитного Диполя Герца (МГД), собственно предназначены  быть  используемыми преимущественно  в СДВ диапазоне, а именно, в ОНЧ (3 КГц - 30 КГц), КНЧ (30 Гц - 3000 Гц) и НЧ (3 КГц -  80 КГц) диапазонах частот в поглощающих  средах с удельным сопротивлением Ω среды менее 40 Ом м, включая морскую воду,  для которой  Ω = 0.3 Ом м.

С "Радиотехнической" точки зрения в среде, для которой относительные величины магнитной μ_r  и электрической ε_r  проницаемости отличны от единицы

можно было утверждать, что "Волновое сопротивление" W в такой среде будет иметь значение:  (1 - 1), где  (1 -2), а  длина волны казалось бы можно было бы вычислять по формуле  (1 - 3),

где λ , λ₀  - соответственно длина волны в среде и длина волны в вакууме.

W₀  - Волновое сопротивление вакуума. μ₀ - магнитная проницаемость вакуума,

μ₀ = 4π10^-7 Генри / м (1 - 3), ε₀ = 1/36π10⁹ Фарад / м  (1 - 4)

Например, при нахождении в морской среде μ_r  =1 (1 - 5),  ε_r  = 81 (1 - 6), поэтому можно считать, что W =  41.89 Ом,  (1 - 6), и можно было бы предположить, что λ = (λ₀ / 9) м (1 - 7).

Однако  исследовании прохождения электромагнитных волн несущей частоты f  в случае нахождения  Передающей или Приёмной Линейной Электрической Антенн в реальной Земной среде  геофизиками Компании "РАДИОНДА" [4] (подробную информацию о научно - технической деятельностью их сотрудников можно ознакомиться на их сайте: www.radionda.ru) и при объяснении ими применённого инновационного метода диагностики недр Земли были приведены: а)формула оценки длины волны в среде, обладающей конечным значением величины Ω:

   (1 - 8).

и б) коэффициента затухания к амплитудных значений Е_φm, Н_ρm,  Н_θm  

 (1 - 9)               при 2πfΩε<1

Поэтому представляет интерес рассмотреть создаваемое находящейся погружённой в такого рода среду ПЛМА во круг себя электромагнитное поле.

Для анализа (см. Изо. 1) использованы [3] следующие выражения отыскания амплитудных значений электрической Е_φm и магнитных Н_ρm,  Н_θm составляющих напряжённостей электромагнитного поля, создаваемого моделью ЛМА №21 с помощью выражений

J_m -  "Магнитный ток" протекаемый в теле ПЛМА, [В];

λ - длина волны поглощающей среды в которую погружена модель ПЛМА, [м];

к - коэффициент затухания  в среде  конечном значении величины Ω[Ом м] в [1/м];

При рассмотрении затухания плоской моно гармоничной электромагнитной волны частоты f с помощью Уравнений Максвелла в среде с  значением Ω  (в частности, для морской среды  при температуре 25 ⁰ С  Ω = 0.3 Ом м) оценка величины h толщины слоя затухания в e - раз амплитудного значения электрической E [В/м] и магнитной Н [А/м] составляющих напряженностей электромагнитного поля может быть вычислена по формуле, любезно представленной доцентом, кандидатом физ. - мат. наук Павлом Юрьевичем Пушкарёвым (подробнее о нём - www.spectra- geo.narod.ru/CV_Ru.htm)

(1 - 15),

где h[м] - слой затухания составляющей Напряжённости Магнитного Н [А/м] или Электрического E [В/м] электромагнитного поля в 2.71 раз.

Поэтому  (1 - 10), и соответственно, 

 (1 - 11),

где ρ [м] - расстояние до приёмного устройства от места расположения ПЛМА.

По Ю.П. Пушкарёву коэффициент затухания к  электрической Е_φm  и магнитных Н_ρm, Н_θm компонент электромагнитного поля [1/м]:

 (1 - 12)

С учётом μf = W / λ (1 - 12)

выражения (1 - 10, 11, 12) принимают вид [3]: 

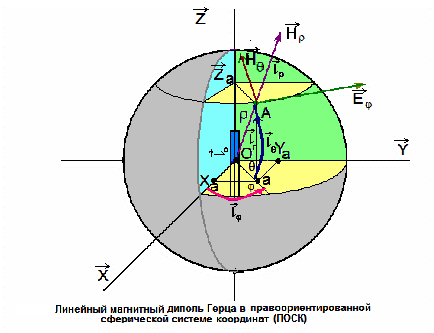
Изо.1.

2. Как было отмечено в [3]  данная модель ЛМА №21 

Фото 1. На переднем плане вид модели ЛМА№21 и модель резонансный конденсатора для частоты 30 КГц, рассчитанные для работы при I_am до 8 А [3] .

до настоящего момента проходит испытания у геофизиков Компании "Радионда" совместно  с приёмной ферритовой антенной МА№2.

В Феврале 2016 г сотрудниками Компании "Радионда"  были погружены в герметичных корпусах передающей и приёмных антенн оборудования Компании геофизиков "Радионда" Модель ЛМА№21 и Модель МА№2 в две, расположенные на расстоянии ρ = 17.5 м (2 - 1)

друг от друга, вертикальные скважины на глубину до 18 м. При этом они погружались  синхронно вертикально друг против друга с заданным шагом с помощью специальных устройств "опускания - подъёма" на полигоне Геофизического Факультета  МГУ в Московской области с заранее известными  свойствами слоёв пород грунта на заданной глубине.

В полученном Отчёте Компанией "ЛРЭТ" (данных испытаний Моделей ЛМА №21  и МА№2 на частоте 29550 Гц) , в частности, при нахождении на глубине 12 м друг относительно друга указаны электрические характеристики породы грунта:

ε_r = 10 ,  μ_r = 1, Ω = 20 Ом м  (2 - 2), и что для частоты f  = 30 КГц в данной среде длина волны λ = 81.36 м  (3 - 3), а коэффициент поглощения к = 0.077   (2 - 4)  при значении I_am тока возбуждения продольного  магнитного поля в  теле ЛМА №21, поданного  на обмотку его соленоида, на частоте  29550 Гц:  I_am = 0.62 А  (2 - 5)

Использование формулы (1 - 9) дало значение к = 0.0769  (2 -6).

На выходе пассивной модели МА№2 был зарегистрирован  моно гармоничный сигнал  частоты 30 КГц со значением напряжения  U_mвых = 5039 мкВ (2 -6).

Поскольку была Приёмная Ферритовая Антенна МА№2 обёрнута ими тонкой металлической фольгой,  как они считают - входной контур, используемого ими предусилителя приёмного устройства, обладал добротностью  Q =3 (2 - 7), поэтому они считают, что был зарегистрирован МА№2 сигнал U_МА№2 = 1680 мкВ (2 - 8). 

Фото. 2. Модель МА№2 в герметичном кожухе, а выше справа Рамочная приёмная антенна ЛА№1 (А_ефф = 0.25 кв.м, N=100 витков).

Как было отмечено в [3] формула для расчета значения "Действующей высоты" Н_эфф  [м]

Приёмной Рамочной  ЛА№1:

 (2 - 9) В свободном пространстве (вакууме) для частоты 29550 Гц  λ₀ = 10150.3 м  (2 - 10),  а в упомянутой среде испытания антенн ЛМА№21 и МА№2 длина волны, вычисленная по формуле (1 - 8), λ = 82.27 м (2 - 10)

Поэтому для Антенны ЛА№1 при длине λ₀ = 10150.3 м Н_{ЛА№1эфф} = 0.0155м (2 - 11),

а при λ = 82.27 м   Н_{ЛА№1эфф} = 1.91 м  (2 - 12).

Измерения автора показали, что в отсутствии магнитопровода на частоте f = 1 КГц индуктивность  обмотки соленоида ЛМА№ 21 L_o = 10.27 мкГн  (2 - 13), а в присутствии магнитопровода внутри тела ЛМА№21 на частоте 29550 Гц - индуктивность обмотки соленоида L_а = 541.6 мкГн (2 - 14).

Это значит, что эффективное значение относительной величины магнитной проницаемости Модели ЛМА№21 μ_эфф = 52.7 (2 - 15)

Автором проводились измерения величины регистрации электромагнитного излучения   Модели ЛМА№21 одновременно с одного и того же места  с расстояния 14 метров антеннами ЛА№1 и МА№2 с целью определения отношения величин их "Действующей высоты" для частоты 29550 Гц.

Измерения показали, что для λ₀ = 10150.3 м   Н_{МА№2эфф} = 0.017 м  (2 - 13), поэтому  

для среды, в которой  λ = 82.27 м   Н_{МА№2эфф} = 2.16 м  (2 - 14).

3. Анализ работы модели ЛМА№21 [3]  в поглощающей среде на частоте 29550 Гц при ε_r = 10,  μ_r = 1, Ω = 20 Ом м (3 - 1).

С учётом основных данных для модели ЛМА№ 21, указанных в статье автора [3], по формулам (1 - 13, 14, 15) с учётом значения λ, вычисленного на глубине 12 м  (3 - 2) по формуле  (1 - 8), и с учётом  значения для коэффициента к, вычисленного по формуле (1 - 9)  для расстояния ρ = 17.5 м  (3 - 3) между антенной ЛМА"21 и МА№2  для частоты 29550 Гц можно с помощью программы "MathCAD MathSoft, Inc."[5] рассчитать значение J_m| и  амплитудные значения Е_φm, Н_ρm,  Н_θm. 

Так как для данной среды а) вычисления по формуле (1 - 1)  дают  значение  "Волнового сопротивления" W =  119.22 Ома (3 - 4),

б)  результат расчёта по формуле (1 -9) коэффициента затухания к: к = 0.076 [1/м] (3 - 5). 

в) Расчёт коэффициента α_g по формуле α_g =2π/λ  (3 - 6): α_g =0.076 [1/м] (3 - 7)

г) В момент резонанса на частоте f_o = 29550 Гц реактивное сопротивление X_а  индуктивности обмотки соленоида ЛМА№ 21 L_а равно  = i100.56 Ом (3 - 8)

д) тесты антенного контура последовательного резонанса показали, что было получено значение полосы пропускания BW =557. 5 Гц  (3 - 9) на уровне - 3 dB, поэтому Эффективное значение добротности  = 53 (3 - 10).

е) Ёмкость С резонансного конденсатора контура антенного тока I_am = 0.62 А  (2 - 5) "возбуждения" продольного магнитного потока ЛМА№21 определяется как:

 (3 - 11)  С=53.56 нФ (3 - 12).

ж) Амплитуда напряжение U_am  на обмотке соленоида ЛМА№ 21 в момент резонанса:

 = i 62.34 В ( 3 - 13).

з) Амплитудное значение циркулирующей вокруг боковой поверхности соленоида ЛМА№21 напряжённости электрического поля определяется как

= i 11.25 В/м (3 - 14).

и) Амплитудное значение "магнитного тока" J_am  находят из равенства

= (- 9.74 10 ^{- 6} + i 0.445)В   (3 - 15)

Были получены следующие выражения для  Е_φm, Н_ρm, Н_θm для дистанции ρ=17.5 м и θ = 0

 = (1.59 10 ^-5 + i 7.6 10 ^{- 6} ) В/м  (3 - 16)

|E_φm| =1 7.6 мкВ/м  (3 - 17).

 = (2.653 10 ^{- 5} +  i 2.4 10 ^-7) А/м  (3 - 17)

|H_θm| = 26.53 мкА/м  (3 - 18)

Естественно, что при θ = 0

|Н_ρm| = 0  (3 - 19).

Так как Н_{МА№2эфф} = 2.164 м, то  U1_{МА№2 вых} = Н_{МА№2эфф} |E_φm| = 38 мк В  (3 - 19)

и U2_{МА№2 вых} = |H_θm| W Н_{МА№2эфф} =  6.839 мВ   (3 - 20) 

4. Заключение

1. Видим, что при    ρ= 17.5 м и  λ = 82.27 м для ЛМА№21 и МА№2, -  как типичных представителя МГД в рассматриваемой среде, - вклад  в значение напряжения, регистрируемое Приёмной магнитной или Рамочной антенной, играет лишь магнитная составляющая напряжённости поля, а не Электрическая составляющая потока электромагнитных волн и, что самое главное: в данной среде  на данной дистанции происходит уже процесс излучения  Моделью МА №21 электромагнитного поток, так как распространение сферических волн проходит  (по крайней мере в месте регистрации) в так называемой "Дальней зоне"в силу выполнения условия    ρ= 17.5 м) <  (λ = 82.27 м) / 2π =  13.1 м).

2. Теоретическое значение для ЭДС = 6.84 мВ на выходе пассивной Модели Магнитной Антенны, условно названной МА № 2, чуть выше практически зарегистрированного ей значения в момент испытания геофизиками Компании"РАДИОНДА" [4]   в скважинах Испытательного полигона Геофизического Факультета МГУ в реальных условиях в Феврале 2016 г.(см. Фото.3, любезно представленное автору по электронной почте).

Фото. 3. Геофизики Компании "Радионда" в момент погружения антенных корпусов, в которых находятся Модель ЛМА № 21 и Модель МА№ 2 в скважины Испытательного полигона Геологического Факультета МГУ в Московской Области во время теста

Литература:

1. Arie Lyasko"Теоретическое приложение и инженерный метод расчёта"  US Patent 4458248 Jul.3.1984. "Parametric Antenna".

2. А.Б. Ляско, Описание  изобретения, Патент РФ № 2428774 от 10 Сентября 2010 г., "Передающие Линейные Магнитные  Антенны (ЛМА)".

3. А.Б. Ляско, "Сферические волны передающих Линейных Магнитных Антенн (Часть I), "Евразийский Научный Журнал", № 6, 2016 г.

4. Труды геофизиков Компании "Радионда"( Например, "Канадская презентация" 2002 г., "Предварительный Отчёт испытаний в Феврале 2016 г.").

5. Программа "MathCAD, V. 7.0, MathSoft, Inc.