–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ш–Ј—Г—З–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П –Љ–µ—В–∞–ї–ї–Њ—А–µ–ґ—Г—Й–Є—Е —Б—В–∞–љ–Ї–Њ–≤ —Б —Г—З–µ—В–Њ–Љ –≤–ї–Є—П–љ–Є—П –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–≤—П–Ј–Є, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–є –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П
–†—Г–±—А–Є–Ї–∞: –Ґ–µ—Е–љ–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: « –Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ9 2022» (—Б–µ–љ—В—П–±—А—М, 2022)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 718
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ш–Ј—Г—З–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П –Љ–µ—В–∞–ї–ї–Њ—А–µ–ґ—Г—Й–Є—Е —Б—В–∞–љ–Ї–Њ–≤ —Б —Г—З–µ—В–Њ–Љ –≤–ї–Є—П–љ–Є—П –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–≤—П–Ј–Є, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–є –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П
–Э–≥—Г–µ–љ –Э–≥–Њ–Ї –С–Є–љ—М,
–Р—Б–њ–Є—А–∞–љ—В
–§–∞–Љ –Ф–Є–љ—М –Ґ—Г–љ–≥
–і–Њ—Ж, –і.—В.–љ,
–Т—М–µ—В–љ–∞–Љ—Б–Ї–Є–є –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ—Л–є —В–µ—Е–љ–Є—З–µ—Б–Ї–Є–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В
–Є–Љ–µ–љ–Є –Ы–µ –Ъ—Г–є –Ф–Њ–љ–∞
–Р–љ–љ–Њ—В–∞—Ж–Є—П.
–Ф–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ –њ—А–Є–≤–Њ–і–∞ –Є—Б–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤, –њ—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ, –њ—А–Є–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П –Ј–∞ —Б—З—С—В —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –Љ–Њ–≥—Г—В —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –Љ–µ–љ—П—В—М —Б–≤–Њ–Є —Б–≤–Њ–є—Б—В–≤–∞. –Т —Н—В–Њ–є —Б—В–∞—В—М–Є –њ—А–µ–і–ї–∞–≥–∞—О—В—Б—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –Љ–Њ–і–µ–ї–Є –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –њ—А–Њ–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П, –љ–∞–њ—А–Є–Љ–µ—А, –љ–∞ —В–Њ–Ї–∞—А–љ–Њ–Љ —Б—В–∞–љ–Ї–µ —Б —Г—З–µ—В–Њ–Љ –≤–ї–Є—П–љ–Є—П –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П. –Я—А–Є —Н—В–Њ–Љ –љ–µ–ї–Є–љ–µ–є–љ–∞—П –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–∞—П —Б–≤—П–Ј—М, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–∞—П –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П, –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В—Б—П –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л. –Ю–љ–∞ –Ј–∞–≤–Є—Б–Є—В –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞, –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є –Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –і–≤–Є–≥–∞—В–µ–ї—П. –Я—А–Є–≤–µ–і–µ–љ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ —Б–Є—Б—В–µ–Љ—Л. –С—Л–ї–Њ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ –љ–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є—Е —Б–≤–Њ–є—Б—В–≤ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ–µ –≤–ї–Є—П–љ–Є–µ –Њ–Ї–∞–Ј—Л–≤–∞–µ—В —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–Њ–Љ–Є–љ–∞–ї—М–љ–Њ–є –Љ–Њ—Й–љ–Њ—Б—В–Є –і–≤–Є–≥–∞—В–µ–ї–µ–є –Є –Љ–Њ—Й–љ–Њ—Б—В–Є –њ—А–Њ—Ж–µ—Б—Б–∞ –Њ–±—А–∞–±–Њ—В–Ї–Є. –Х—Б–ї–Є –Љ–Њ—Й–љ–Њ—Б—В—М –і–≤–Є–≥–∞—В–µ–ї—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –±–Њ–ї—М—И–µ –Љ–Њ—Й–љ–Њ—Б—В–Є —А–µ–Ј–∞–љ–Є—П, —В–Њ —А–µ–∞–Ї—Ж–Є–µ–є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –Њ–±—А–∞–±–Њ—В–Ї–Є –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М. –Т –њ—А–Њ—В–Є–≤–љ–Њ–Љ —Б–ї—Г—З–∞–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞, –љ–∞–њ—А–Є–Љ–µ—А, –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П, —Б—В–∞–љ–Њ–≤–Є—В—Б—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –љ–µ–ї–Є–љ–µ–є–љ–Њ–є. –Я—А–Є –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л—Е —А–µ–ґ–Є–Љ–∞—Е –љ–µ–ї–Є–љ–µ–є–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї—Г—О —Б–≤—П–Ј—М, —П–≤–ї—П—О—В—Б—П –љ–µ–Њ–і–љ–Њ–Ј–љ–∞—З–љ—Л–Љ–Є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –і–≤–Є–≥–∞—В–µ–ї—П –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ —В—А–µ—Е —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –Њ–і–љ–∞ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е —П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є; –њ–Њ –Љ–µ—А–µ —Г–≤–µ–ї–Є—З–µ–љ–Є—П –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –љ–∞–±–ї—О–і–∞–µ—В—Б—П –±–Є—Д—Г—А–Ї–∞—Ж–Є—П —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л —В–Є–њ–∞ –≤–Є–ї–Ї–Є, —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Њ–±–ї–∞–і–∞—О—В –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–є –Њ–±–ї–∞—Б—В—М—О –њ—А–Є—В—П–ґ–µ–љ–Є—П.
–Ъ–ї—О—З–µ–≤–Њ–µ —Б–ї–Њ–≤–Њ. –Ф–Є–љ–∞–Љ–Є–Ї–∞ –њ—А–Є–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П, –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П, —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ, –±–Є—Д—Г—А–Ї–∞—Ж–Є—П, –Њ–±–ї–∞—Б—В—М –њ—А–Є—В—П–ґ–µ–љ–Є—П.
–Т–≤–µ–і–µ–љ–Є–µ
–Ь–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П –Њ–±—А–∞–±–Њ—В–Ї–∞ –љ–∞ –Љ–µ—В–∞–ї–ї–Њ—А–µ–ґ—Г—Й–Є—Е —Б—В–∞–љ–Ї–∞—Е –Є–Љ–µ–µ—В —А–µ—И–∞—О—Й–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –і–ї—П –њ—А–Њ–Є–Ј–≤–Њ–і—Б—В–≤–µ–љ–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –Њ–±—К–µ–Љ–∞ –Є –Ј–∞—В—А–∞—В. –°—В–∞–±–Є–ї—М–љ–Њ—Б—В—М –і–≤–Є–ґ–µ–љ–Є–є –Є—Б–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤, –Ј–∞–і–∞–≤–∞–µ–Љ—Л—Е –њ—А–Є–≤–Њ–і–∞–Љ–Є, —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Є–Љ –Є–Ј –љ–∞–Є–±–Њ–ї–µ–µ –≤–∞–ґ–љ—Л—Е —Д–∞–Ї—В–Њ—А–Њ–≤ –і–ї—П —А–∞–±–Њ—В—Л —Б—В–∞–љ–Ї–Њ–≤, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –µ–µ –њ–Њ–≤–µ–і–µ–љ–Є–µ –љ–∞–њ—А—П–Љ—Г—О –≤–ї–Є—П–µ—В –љ–∞ —Б—А–Њ–Ї —Б–ї—Г–ґ–±—Л —Б—В–∞–љ–Ї–∞, —В–Њ—З–љ–Њ—Б—В—М –Є –Ї–∞—З–µ—Б—В–≤–Њ –Є–Ј–≥–Њ—В–Њ–≤–ї—П–µ–Љ–Њ–≥–Њ –Є–Ј–і–µ–ї–Є—П. –Я—А–Є –њ—А–Њ–µ–Ї—В–Є—А–Њ–≤–∞–љ–Є–Є —Г–њ—А–∞–≤–ї—П–µ–Љ—Л—Е –њ—А–Є–≤–Њ–і–Њ–≤ –Љ–µ—В–∞–ї–ї–Њ—А–µ–ґ—Г—Й–Є—Е —Б—В–∞–љ–Ї–Њ–≤ –њ—А–Є–љ–Є–Љ–∞—О—В –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ –Љ–Њ–Љ–µ–љ—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П, –і–µ–є—Б—В–≤—Г—О—Й–Є–є –љ–∞ —А–Њ—В–Њ—А –і–≤–Є–≥–∞—В–µ–ї—П, –Ї–∞–Ї –љ–µ–Ї–Њ—В–Њ—А—Г—О –њ–Њ—Б—В–Њ—П–љ–љ—Г—О –≤–µ–ї–Є—З–Є–љ—Г –Є–ї–Є –Ј–∞–і–∞–љ–љ—Г—О —Д—Г–љ–Ї—Ж–Є—О –≤—А–µ–Љ–µ–љ–Є –≤–љ–µ—И–љ–µ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П. –Ю–і–љ–∞–Ї–Њ –Љ–Њ–Љ–µ–љ—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л, —В–∞–Ї –Ї–∞–Ї –Њ–љ, –≤ –Њ—Б–љ–Њ–≤–љ–Њ–Љ —Д–Њ—А–Љ–Є—А—Г–µ—В—Б—П —Б–Є–ї–∞–Љ–Є —А–µ–Ј–∞–љ–Є—П, –≤ —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, —Б–Є–ї—Л —А–µ–Ј–∞–љ–Є—П –Ј–∞–≤–Є—Б–Є—В –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Є—Б—В–µ–Љ—Л. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ —Б–Є–ї—Л —А–µ–Ј–∞–љ–Є—П –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л –Њ–±–ї–∞–і–∞–µ—В –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М—О.
–Э–µ–ї–Є–љ–µ–є–љ—Л–є –∞–љ–∞–ї–Є–Ј –і–Є–љ–∞–Љ–Є–Ї–Є —И–њ–Є–љ–і–µ–ї—П –±—Л–ї –њ—А–Њ–≤–µ–і–µ–љ –і–ї—П –њ–Њ–≤—Л—И–µ–љ–Є—П –Ї–∞—З–µ—Б—В–≤–∞ –Є–Ј–≥–Њ—В–Њ–≤–ї—П–µ–Љ–Њ–≥–Њ –Є–Ј–і–µ–ї–Є—П. –Т–Є–±—А–∞—Ж–Є–Є —Б—В–∞–љ–Ї–∞ –і–ї—П –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ–≥–Њ —А–µ–Ј–∞–љ–Є—П –±—Л–ї–Є –Њ—Е–∞—А–∞–Ї—В–µ—А–Є–Ј–Њ–≤–∞–љ—Л —Б –њ–Њ–Љ–Њ—Й—М—О –±–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–Њ–є –і–Є–∞–≥—А–∞–Љ–Љ—Л (Dombovari –Є –і—А, 2008). –Т–Є–±—А–∞—Ж–Є—П –≤ —Б–Є—Б—В–µ–Љ–µ —И–њ–Є–љ–і–µ–ї—П –њ—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞–љ–∞ —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –і–Є–љ–∞–Љ–Є–Ї–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П (Cao et al., 2012), –Ї–Њ–≥–і–∞ –љ–µ–±–Њ–ї—М—И–∞—П –≤–Є–±—А–∞—Ж–Є—П –і–Њ–њ—Г—Б—В–Є–Љ–∞. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –≤–Є–±—А–∞—Ж–Є—П —Б—В–∞–љ–Ї–∞ –±—Л–ї–∞ –Є–Ј—Г—З–µ–љ–∞ —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Є –•–Њ–њ—Д–∞ –і–ї—П —Б–Є—Б—В–µ–Љ—Л –Ј–∞–і–µ—А–ґ–Ї–Є (Xie et al., 2012). –С—Л–ї–∞ –њ—А–µ–і–ї–Њ–ґ–µ–љ–∞ —Б–Є—Б—В–µ–Љ–∞ —И–њ–Є–љ–і–µ–ї—П –і–ї—П –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П –і–Є–∞–≥—А–∞–Љ–Љ—Л –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є –њ—Г—В–µ–Љ –Є–љ—В–µ–≥—А–∞—Ж–Є–Є —И–њ–Є–љ–і–µ–ї—П, –Ј–∞–≤–Є—Б—П—Й–µ–≥–Њ –Њ—В —Б–Ї–Њ—А–Њ—Б—В–Є. –Я–µ—А–µ–і–∞—В–Њ—З–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П —Б—В–∞–±–Є–ї—М–љ–Њ—Б—В–Є –≤–Є–±—А–∞—Ж–Є–Є (Gagnol et al., 2007). –Р–љ–∞–ї–Є–Ј –≤–Њ–Ј–Љ—Г—Й–µ–љ–Є–є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є —И–њ–Є–љ–і–µ–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л (Canniere et al., 1981), –њ—А–Є —Н—В–Њ–Љ –∞–љ–∞–ї–Є–Ј —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є –Љ–Њ–ґ–љ–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —В–Њ–ї—М–Ї–Њ –і–ї—П –Љ–∞–ї—Л—Е –Ј–љ–∞—З–µ–љ–Є–є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤. Jemielniak and Widota (1984) –њ—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞–ї–Є –≤–ї–Є—П–љ–Є–µ –Є–Ј–Љ–µ–љ–µ–љ–Є–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –љ–∞ —Б—В–∞–±–Є–ї—М–љ–Њ—Б—В—М –Њ–±—А–∞–±–Њ—В–Ї–Є —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –∞–Љ–њ–ї–Є—В—Г–і–љ–Њ–≥–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞. –Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —Г—Б–Є–ї–µ–љ–Є—П –∞–Љ–њ–ї–Є—В—Г–і—Л –±—Л–ї –њ–Њ–ї—Г—З–µ–љ –і–ї—П –Њ–і–љ–Њ–є —З–∞—Б—В–Њ—В—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є –±–µ–Ј —Г—З–µ—В–∞ –≤–ї–Є—П–љ–Є—П –љ–∞ –љ–Њ–Љ–Є–љ–∞–ї—М–љ—Г—О —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П. Jayaram –Є –і—А (2000) –њ—А–µ–і—Б—В–∞–≤–Є–ї–Є –∞–љ–∞–ї–Є–Ј —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є —Б–Є—Б—В–µ–Љ—Л —И–њ–Є–љ–і–µ–ї—П —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –ї–Є–љ–µ–є–љ–Њ–≥–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П —Б –Є–Ј–Љ–µ–љ—П—О—Й–Є–Љ—Б—П –≤–Њ –≤—А–µ–Љ–µ–љ–Є –Ј–∞–њ–∞–Ј–і—Л–≤–∞–љ–Є–µ–Љ. HuihuiMiao –Є –і—А (2022) –Є—Б—Б–ї–µ–і–Њ–≤–∞–ї–Є –≤–ї–Є—П–љ–Є–µ –љ–µ–ї–Є–љ–µ–є–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –Ї–Є–љ–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е —Б–Њ–µ–і–Є–љ–µ–љ–Є–є –љ–∞ –і–Є–љ–∞–Љ–Є–Ї—Г —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–ї–Њ–љ–љ–∞-—И–њ–Є–љ–і–µ–ї—М. –Т –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–Є Juan Xu –Є –і—А –±—Л–ї–Є –Є–Ј—Г—З–µ–љ—Л –≤–Є–±—А–∞—Ж–Є–Њ–љ–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є —А–µ–∞–Ї—Ж–Є–Є –љ–∞ –і–Є—Б–±–∞–ї–∞–љ—Б —Б–Є—Б—В–µ–Љ—Л —И–њ–Є–љ–і–µ–ї—П.
–Т –Њ—В–ї–Є—З–Є–µ –Њ—В –њ—А–Є–≤–µ–і–µ–љ–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є, –≤ —Н—В–Њ–є —Б—В–∞—В—М–Є –±—Л–ї–Њ –њ—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞–љ–Њ –≤–ї–Є—П–љ–Є–µ —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ –і–Є–љ–∞–Љ–Є–Ї—Г –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П. –Ф–ї—П —Н—В–Њ–≥–Њ, –њ—А–µ–і–ї–∞–≥–∞—О—В—Б—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –Љ–Њ–і–µ–ї–Є –і–Є–љ–∞–Љ–Є–Ї–Є —И–њ–Є–љ–і–µ–ї—П —Б —Г—З–µ—В–Њ–Љ –≤–ї–Є—П–љ–Є–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–≤—П–Ј–Є, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–є –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П. –≠—В–∞ –љ–µ–ї–Є–љ–µ–є–љ–∞—П —Б–≤—П–Ј—М –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В—Б—П –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л. –Ю–љ–∞ –Ј–∞–≤–Є—Б–Є—В –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞, –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є –Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –і–≤–Є–≥–∞—В–µ–ї—П. –Я—А–Є–≤–µ–і–µ–љ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ —Б–Є—Б—В–µ–Љ—Л, –≤ —В–Њ–Љ —З–Є—Б–ї–µ, –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ–±–Є. –І–Є—Б–ї–µ–љ–љ–Њ –∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞—В—М –Є–Ј–Љ–µ–љ–µ–љ–Є–µ —Д–∞–Ј–Њ–≤—Л—Е –њ–Њ—В—А–µ—В–Њ–≤ —Б–Є—Б—В–µ–Љ—Л.
2. –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П –Љ–Њ–і–µ–ї—М
–Я—А–Є –∞–љ–∞–ї–Є–Ј–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–Њ–≤ –љ–∞ –Љ–µ—В–∞–ї–ї–Њ—А–µ–ґ—Г—Й–Є—Е —Б—В–∞–љ–Ї–∞—Е –≥–ї–∞–≤–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Є–Љ–µ—О—В –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В–Є –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є—П —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є —Б –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ –Њ–±—А–∞–±–Њ—В–Ї–Є. –Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Г—З–Є—В—Л–≤–∞—В—М, —З—В–Њ —А–µ–∞–Ї—Ж–Є—П —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –њ—А–Њ—П–≤–ї—П–µ—В—Б—П, –њ—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ, –≤ –њ—А–Є–≤–Њ–і–∞—Е –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П. –≠—В–Њ —Б–≤—П–Ј–∞–љ–Њ —Б —В–µ–Љ, —З—В–Њ –њ—А–Є–≤–Њ–і—Л –њ–Њ–і–∞—З–Є —Б—Г–њ–њ–Њ—А—В–Њ–≤ –Є–Љ–µ—О—В –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї—Г—О —З–∞—Б—В—М —Б –±–Њ–ї—М—И–Є–Љ –њ–µ—А–µ–і–∞—В–Њ—З–љ—Л–Љ –Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ. –Я–Њ—Н—В–Њ–Љ—Г –Њ–≥—А–∞–љ–Є—З–Є–Љ—Б—П, —Б–ї—Г—З–∞–µ–Љ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є—П —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї—П –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П —Б –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П (—А–Є—Б. 1). –С—Г–і–µ–Љ —Б—З–Є—В–∞—В—М —П–Ї–Њ—А—М –і–≤–Є–≥–∞—В–µ–ї—П —И–њ–Є–љ–і–µ–ї—П, –ґ—С—Б—В–Ї–Њ —Б–Њ–µ–і–Є–љ—С–љ–љ—Л–Љ —Б–Њ —И–њ–Є–љ–і–µ–ї–µ–Љ. –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П –Є–Љ–µ–µ—В –≤–Є–і

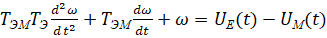 (1)
(1)
–≥–і–µ 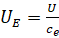 - –љ–∞–њ—А—П–ґ–µ–љ–Є–µ —П–Ї–Њ—А—П, –њ—А–Є–≤–µ–і–µ–љ–љ–Њ–µ –Ї —З–∞—Б—В–Њ—В–µ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П;
- –љ–∞–њ—А—П–ґ–µ–љ–Є–µ —П–Ї–Њ—А—П, –њ—А–Є–≤–µ–і–µ–љ–љ–Њ–µ –Ї —З–∞—Б—В–Њ—В–µ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П; 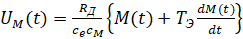 - –Љ–Њ–Љ–µ–љ—В, –і–µ–є—Б—В–≤—Г—О—Й–Є–є –љ–∞ —А–Њ—В–Њ—А –і–≤–Є–≥–∞—В–µ–ї—П, –њ—А–Є–≤–µ–і—С–љ–љ—Л–є –Ї —З–∞—Б—В–Њ—В–µ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П;
- –Љ–Њ–Љ–µ–љ—В, –і–µ–є—Б—В–≤—Г—О—Й–Є–є –љ–∞ —А–Њ—В–Њ—А –і–≤–Є–≥–∞—В–µ–ї—П, –њ—А–Є–≤–µ–і—С–љ–љ—Л–є –Ї —З–∞—Б—В–Њ—В–µ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П; 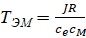 ,
, 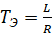 ,
, 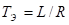 - —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —Н–ї–µ–Ї—В—А–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П –Є —Н–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–∞—П –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –≤—А–µ–Љ–µ–љ–Є;
- —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —Н–ї–µ–Ї—В—А–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П –Є —Н–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–∞—П –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –≤—А–µ–Љ–µ–љ–Є;  ,
, 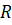 ,
, 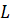 - —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Љ–Њ–Љ–µ–љ—В –Є–љ–µ—А—Ж–Є–Є, –њ—А–Є–≤–µ–і—С–љ–љ—Л–є –Ї —А–Њ—В–Њ—А—Г –і–≤–Є–≥–∞—В–µ–ї—П, —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ –Є –Є–љ–і—Г–Ї—В–Є–≤–љ–Њ—Б—В—М —Ж–µ–њ–Є —П–Ї–Њ—А—П;
- —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Љ–Њ–Љ–µ–љ—В –Є–љ–µ—А—Ж–Є–Є, –њ—А–Є–≤–µ–і—С–љ–љ—Л–є –Ї —А–Њ—В–Њ—А—Г –і–≤–Є–≥–∞—В–µ–ї—П, —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ –Є –Є–љ–і—Г–Ї—В–Є–≤–љ–Њ—Б—В—М —Ж–µ–њ–Є —П–Ї–Њ—А—П; 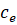 ,
, 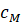 - –њ–∞—А–∞–Љ–µ—В—А—Л –і–≤–Є–≥–∞—В–µ–ї—П;
- –њ–∞—А–∞–Љ–µ—В—А—Л –і–≤–Є–≥–∞—В–µ–ї—П;  —З–∞—Б—В–Њ—В–∞ —И–њ–Є–љ–і–µ–ї—П;
—З–∞—Б—В–Њ—В–∞ —И–њ–Є–љ–і–µ–ї—П; 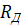 - —А–∞–і–Є—Г—Б –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є –≤ —В–Њ—З–Ї–µ –Ї–Њ–љ—В–∞–Ї—В–∞ —Б –љ–µ–є —А–µ–ґ—Г—Й–µ–≥–Њ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞.
- —А–∞–і–Є—Г—Б –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є –≤ —В–Њ—З–Ї–µ –Ї–Њ–љ—В–∞–Ї—В–∞ —Б –љ–µ–є —А–µ–ґ—Г—Й–µ–≥–Њ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞.

–†–Є—Б. 1. –°—Е–µ–Љ–∞ —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П –Љ–Њ–Љ–µ–љ—В–∞ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л —А–µ–Ј–∞–љ–Є—П

–†–Є—Б. 2. –°—Е–µ–Љ–∞ —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П –њ–ї–Њ—Й–∞–і–Є —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П
–Ф–ї—П –њ–Њ–ї–љ–Њ–≥–Њ —А–∞—Б–Ї—А—Л—В–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П (1) –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –Љ–Њ–Љ–µ–љ—В 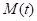 –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л. –Ю–≥—А–∞–љ–Є—З–Є–Љ—Б—П —Б–ї—Г—З–∞–µ–Љ, –Ї–Њ–≥–і–∞ —Г–њ—А—Г–≥–Є–Љ–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є—П–Љ–Є –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ —Б–Є—Б—В–µ–Љ—Л, –Ї–Њ–≥–і–∞ —Б–Ї–Њ—А–Њ—Б—В—М –њ—А–Њ–і–Њ–ї—М–љ–Њ–є –њ–Њ–і–∞—З–Є –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П, –∞ —Б–Ї–Њ—А–Њ—Б—В—М –њ–Њ–њ–µ—А–µ—З–љ—Л—Е –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є–є —Б—Г–њ–њ–Њ—А—В–∞ —А–∞–≤–љ–∞ –љ—Г–ї—О. –Ґ–Њ–≥–і–∞ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–Њ–Љ–µ–љ—В–∞, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П, —Б–љ–∞—З–∞–ї–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —Б–Є–ї—Л, —Д–Њ—А–Љ–Є—А—Г–µ–Љ—Л–µ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П. –Ф–ї—П —Н—В–Њ–≥–Њ, –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ —Б–ї–µ–і—Г—О—Й–Є–µ –≥–Є–њ–Њ—В–µ–Ј—Л [11].
–≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л. –Ю–≥—А–∞–љ–Є—З–Є–Љ—Б—П —Б–ї—Г—З–∞–µ–Љ, –Ї–Њ–≥–і–∞ —Г–њ—А—Г–≥–Є–Љ–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є—П–Љ–Є –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ —Б–Є—Б—В–µ–Љ—Л, –Ї–Њ–≥–і–∞ —Б–Ї–Њ—А–Њ—Б—В—М –њ—А–Њ–і–Њ–ї—М–љ–Њ–є –њ–Њ–і–∞—З–Є –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П, –∞ —Б–Ї–Њ—А–Њ—Б—В—М –њ–Њ–њ–µ—А–µ—З–љ—Л—Е –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є–є —Б—Г–њ–њ–Њ—А—В–∞ —А–∞–≤–љ–∞ –љ—Г–ї—О. –Ґ–Њ–≥–і–∞ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–Њ–Љ–µ–љ—В–∞, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П, —Б–љ–∞—З–∞–ї–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —Б–Є–ї—Л, —Д–Њ—А–Љ–Є—А—Г–µ–Љ—Л–µ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П. –Ф–ї—П —Н—В–Њ–≥–Њ, –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ —Б–ї–µ–і—Г—О—Й–Є–µ –≥–Є–њ–Њ—В–µ–Ј—Л [11].
1. –Ь–Њ–і—Г–ї—М —Б–Є–ї—Л —А–µ–Ј–∞–љ–Є—П –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞ –њ–ї–Њ—Й–∞–і–Є —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П, —В.–µ.
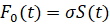 (2)
(2)
–≥–і–µ 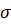 - –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б–Є–ї–∞–Љ–Є –Є –њ–ї–Њ—Й–∞–і—М—О —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П, –Є–Љ–µ—О—Й–Є–є —Б–Љ—Л—Б–ї –і–∞–≤–ї–µ–љ–Є—П, –і–µ–є—Б—В–≤—Г—О—Й–µ–≥–Њ —Б—В—А—Г–ґ–Ї–Њ–є –љ–∞ –њ–µ—А–µ–і–љ—О—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞;
- –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б–Є–ї–∞–Љ–Є –Є –њ–ї–Њ—Й–∞–і—М—О —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П, –Є–Љ–µ—О—Й–Є–є —Б–Љ—Л—Б–ї –і–∞–≤–ї–µ–љ–Є—П, –і–µ–є—Б—В–≤—Г—О—Й–µ–≥–Њ —Б—В—А—Г–ґ–Ї–Њ–є –љ–∞ –њ–µ—А–µ–і–љ—О—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞;  - –њ–ї–Њ—Й–∞–і—М —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–∞—П —Б–ї–µ–і—Г—О—Й–µ–є —Д–Њ—А–Љ—Г–ї–Њ–є
- –њ–ї–Њ—Й–∞–і—М —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–∞—П —Б–ї–µ–і—Г—О—Й–µ–є —Д–Њ—А–Љ—Г–ї–Њ–є
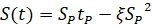 (3)
(3)
–≥–і–µ 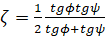 ;
; 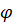 ,
, 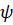 - –њ–µ—А–µ–і–љ–Є–є –Є –Ј–∞–і–љ–Є–є —Г–≥–ї—Л –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞;
- –њ–µ—А–µ–і–љ–Є–є –Є –Ј–∞–і–љ–Є–є —Г–≥–ї—Л –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞; 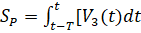 - –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ–і–∞—З–Є –Є–ї–Є –њ—Г—В—М, –њ—А–Њ–є–і–µ–љ–љ—Л–є –≤–µ—А—И–Є–љ–Њ–є –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞ –Ј–∞ –≤—А–µ–Љ—П –Њ–і–љ–Њ–≥–Њ –Њ–±–Њ—А–Њ—В–∞
- –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ–і–∞—З–Є –Є–ї–Є –њ—Г—В—М, –њ—А–Њ–є–і–µ–љ–љ—Л–є –≤–µ—А—И–Є–љ–Њ–є –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞ –Ј–∞ –≤—А–µ–Љ—П –Њ–і–љ–Њ–≥–Њ –Њ–±–Њ—А–Њ—В–∞  ;
; 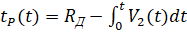 - –≤–µ–ї–Є—З–Є–љ–∞ –њ—А–Є–њ—Г—Б–Ї–∞, –Ј–∞–≤–Є—Б—П—Й–µ–µ –Њ—В –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –≤–µ—А—И–Є–љ—Л –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞ –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї –Њ—Б–Є –≤—А–∞—Й–µ–љ–Є—П –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є (
- –≤–µ–ї–Є—З–Є–љ–∞ –њ—А–Є–њ—Г—Б–Ї–∞, –Ј–∞–≤–Є—Б—П—Й–µ–µ –Њ—В –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –≤–µ—А—И–Є–љ—Л –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞ –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї –Њ—Б–Є –≤—А–∞—Й–µ–љ–Є—П –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є (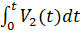 ) –Є —А–∞–і–Є—Г—Б—Г –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є –њ–Њ –Њ—Б–Є –≤—А–∞—Й–µ–љ–Є—П –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞. –Х—Б–ї–Є –≤ –Љ–Њ–Љ–µ–љ—В –≤—А–µ–Ј–∞–љ–Є—П –Є –і–∞–ї–µ–µ
) –Є —А–∞–і–Є—Г—Б—Г –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є –њ–Њ –Њ—Б–Є –≤—А–∞—Й–µ–љ–Є—П –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞. –Х—Б–ї–Є –≤ –Љ–Њ–Љ–µ–љ—В –≤—А–µ–Ј–∞–љ–Є—П –Є –і–∞–ї–µ–µ 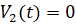 , —В–Њ
, —В–Њ  .
.
2. –С—Г–і–µ–Љ —Б—З–Є—В–∞—В—М —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Г –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–є –Њ—А–Є–µ–љ—В–∞—Ж–Є–Є —Б–Є–ї –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –≤ –њ—А–µ–і–µ–ї–∞—Е –Њ–і–љ–Њ–≥–Њ –Њ–±–Њ—А–Њ—В–∞ –Ј–∞–≥–Њ—В–Њ–≤–Ї–Є, —В–Њ –µ—Б—В—М
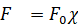 (4)
(4)
–≥–і–µ 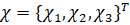 - –≤–µ–Ї—В–Њ—А —Г–≥–ї–Њ–≤—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Њ—А–Є–µ–љ—В–∞—Ж–Є–Є —Б–Є–ї—Л —А–µ–Ј–∞–љ–Є—П, —В.–µ.
- –≤–µ–Ї—В–Њ—А —Г–≥–ї–Њ–≤—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Њ—А–Є–µ–љ—В–∞—Ж–Є–Є —Б–Є–ї—Л —А–µ–Ј–∞–љ–Є—П, —В.–µ. 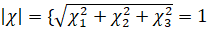 .
.
–Я–Њ–ї–∞–≥–∞—П 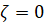 [] –Є
[] –Є  , –Є–Љ–µ–µ–Љ
, –Є–Љ–µ–µ–Љ
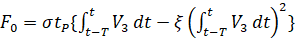 (5)
(5)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞ —Б–Ї–Њ—А–Њ—Б—В—М –њ–Њ–і–∞—З–Є 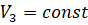 , –∞ –Ј–∞–і–љ–Є–є —Г–≥–Њ–ї ѕИ –Љ–∞–ї, —В–Њ –≤–µ–ї–Є—З–Є–љ–∞
, –∞ –Ј–∞–і–љ–Є–є —Г–≥–Њ–ї ѕИ –Љ–∞–ї, —В–Њ –≤–µ–ї–Є—З–Є–љ–∞ 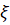 –Љ–∞–ї–∞ –Є –µ—О –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М. –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ (5) –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ
–Љ–∞–ї–∞ –Є –µ—О –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М. –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ (5) –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ
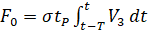 (6)
(6)
–Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ –Љ–Њ–Љ–µ–љ—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –Є–Љ–µ–µ—В –≤–Є–і
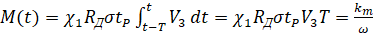 (7)
(7)
–≥–і–µ 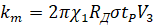 - –љ–µ–Ї–Њ—В–Њ—А—Л–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є–є –≤–ї–Є—П–љ–Є–µ –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ –і–Є–љ–∞–Љ–Є–Ї—Г –њ—А–Њ–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П.
- –љ–µ–Ї–Њ—В–Њ—А—Л–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є–є –≤–ї–Є—П–љ–Є–µ –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ –і–Є–љ–∞–Љ–Є–Ї—Г –њ—А–Њ–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П.
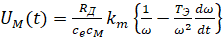 (8)
(8)
–£—А–∞–≤–љ–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ —И–њ–Є–љ–і–µ–ї—П —Б —Г—З–µ—В–Њ–Љ –≤–ї–Є—П–љ–Є—П —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –Є–Љ–µ–µ—В –≤–Є–і
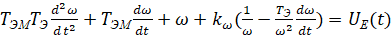 (9)
(9)
–≥–і–µ 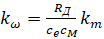 - –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, —Г—З–Є—В—Л–≤–∞—О—Й–Є–є –≤–ї–Є—П–љ–Є–µ —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –љ–∞ –Љ–Њ–Љ–µ–љ—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –≤—А–∞—Й–µ–љ–Є—П —А–Њ—В–Њ—А–∞ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї—П. –Ю–љ –Є–Љ–µ–µ—В —Б–Љ—Л—Б–ї –Ї–≤–∞–і—А–∞—В–∞ —З–∞—Б—В–Њ—В—Л, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–Њ–є –Љ–Њ–Љ–µ–љ—В–Њ–Љ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –≤ —Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–Љ—Б—П —Б–Њ—Б—В–Њ—П–љ–Є–Є.
- –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, —Г—З–Є—В—Л–≤–∞—О—Й–Є–є –≤–ї–Є—П–љ–Є–µ —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –љ–∞ –Љ–Њ–Љ–µ–љ—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –≤—А–∞—Й–µ–љ–Є—П —А–Њ—В–Њ—А–∞ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї—П. –Ю–љ –Є–Љ–µ–µ—В —Б–Љ—Л—Б–ї –Ї–≤–∞–і—А–∞—В–∞ —З–∞—Б—В–Њ—В—Л, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–Њ–є –Љ–Њ–Љ–µ–љ—В–Њ–Љ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –≤ —Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–Љ—Б—П —Б–Њ—Б—В–Њ—П–љ–Є–Є.
–Я–Њ –Љ–µ—А–µ —Г–≤–µ–ї–Є—З–µ–љ–Є—П –Њ—В–љ–Њ—И–µ–љ–Є—П —Б–Ї–Њ—А–Њ—Б—В–Є –њ–Њ–і–∞—З–Є –Ї —Б–Ї–Њ—А–Њ—Б—В–Є —А–µ–Ј–∞–љ–Є—П –Є–Ј–Љ–µ–љ—П–µ—В—Б—П –Ј–љ–∞—З–µ–љ–Є–µ –Ї–Є–љ–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ј–∞–і–љ–µ–≥–Њ —Г–≥–ї–∞ [11]. –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞—О—В —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –Ј–∞–і–љ—О—О –≥—А–∞–љ—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞, –Ї–Њ—В–Њ—А—Л–µ –љ–∞–њ—А–∞–≤–ї–µ–љ—Л –њ—А–Њ—В–Є–≤ —Б–Ї–Њ—А–Њ—Б—В–Є –њ–Њ–і–∞—З–Є. –Я–Њ—Н—В–Њ–Љ—Г –і–ї—П –њ–Њ–ї–љ–Њ–≥–Њ –Њ–њ–Є—Б–∞–љ–Є—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Є —Б–≤–Њ–є—Б—В–≤ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤–≤–µ—Б—В–Є –≤ —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є–µ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –Ј–∞–і–љ—О—О –≥—А–∞–љ—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞.
–С—Г–і–µ–Љ —Б—З–Є—В–∞—В—М, —З—В–Њ —Г–њ—А—Г–≥–Є–µ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞ –Њ—В—Б—Г—В—Б—В–≤—Г—О—В. –Ґ–Њ–≥–і–∞ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –Є–љ—Б—В—А—Г–Љ–µ–љ—В —Б–Њ —Б—В–Њ—А–Њ–љ—Л –µ–≥–Њ –Ј–∞–і–љ–µ–є –≥—А–∞–љ–Є, –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П –і–≤—Г–Љ—П –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П–Љ–Є. –Т–Њ-–њ–µ—А–≤—Л—Е, –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М—О –Ї–Є–љ–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ј–∞–і–љ–µ–≥–Њ —Г–≥–ї–∞ –Њ—В –Њ—В–љ–Њ—И–µ–љ–Є—П —Б–Ї–Њ—А–Њ—Б—В–Є –њ–Њ–і–∞—З–Є –Ї —Б–Ї–Њ—А–Њ—Б—В–Є —А–µ–Ј–∞–љ–Є—П, –≤–Њ-–≤—В–Њ—А—Л—Е, –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М—О —Б–Є–ї –Њ—В —Б–±–ї–Є–ґ–µ–љ–Є—П –Ј–∞–і–љ–µ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞ —Б –Ј–∞–≥–Њ—В–Њ–≤–Ї–Њ–є. –≠—В–Є —Б–Є–ї—Л, –њ—А–Є–≤–µ–і–µ–љ–љ—Л–µ –Ї —З–∞—Б—В–Њ—В–µ –≤—А–∞—Й–µ–љ–Є—П —А–Њ—В–Њ—А–∞ –і–≤–Є–≥–∞—В–µ–ї—П —И–њ–Є–љ–і–µ–ї—П, –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В—Б—П –≤ –≤–Є–і–µ
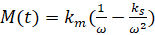 (10)
(10)
–≥–і–µ 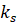 - –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, —Г—З–Є—В—Л–≤–∞—О—Й–Є–є –≤–ї–Є—П–љ–Є–µ —Б–Є–ї, –і–µ–є—Б—В–≤—Г—О—Й–Є—Е –љ–∞ –Ј–∞–і–љ—О—О –≥—А–∞–љ—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞. –Т –≤—Л—А–∞–ґ–µ–љ–Є–Є (10) –њ—А–Є–љ—П—В–Њ –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ –њ–Њ –Љ–µ—А–µ —Г–Љ–µ–љ—М—И–µ–љ–Є—П —З–∞—Б—В–Њ—В—Л —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –Ј–∞–і–љ—О—О –≥—А–∞–љ—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞, —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В—Б—П –±—Л—Б—В—А–µ–µ, —З–µ–Љ —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –њ–µ—А–µ–і–љ—О—О –µ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М. –Ю–±–ї–∞—Б—В—М —Д—Г–љ–Ї—Ж–Є–Є (10) –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —З–∞—Б—В–Њ—В–љ—Л–Љ –і–Є–∞–њ–∞–Ј–Њ–љ–Њ–Љ
- –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, —Г—З–Є—В—Л–≤–∞—О—Й–Є–є –≤–ї–Є—П–љ–Є–µ —Б–Є–ї, –і–µ–є—Б—В–≤—Г—О—Й–Є—Е –љ–∞ –Ј–∞–і–љ—О—О –≥—А–∞–љ—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞. –Т –≤—Л—А–∞–ґ–µ–љ–Є–Є (10) –њ—А–Є–љ—П—В–Њ –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ –њ–Њ –Љ–µ—А–µ —Г–Љ–µ–љ—М—И–µ–љ–Є—П —З–∞—Б—В–Њ—В—Л —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –Ј–∞–і–љ—О—О –≥—А–∞–љ—М –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞, —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В—Б—П –±—Л—Б—В—А–µ–µ, —З–µ–Љ —Б–Є–ї—Л, –і–µ–є—Б—В–≤—Г—О—Й–Є–µ –љ–∞ –њ–µ—А–µ–і–љ—О—О –µ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М. –Ю–±–ї–∞—Б—В—М —Д—Г–љ–Ї—Ж–Є–Є (10) –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —З–∞—Б—В–Њ—В–љ—Л–Љ –і–Є–∞–њ–∞–Ј–Њ–љ–Њ–Љ 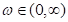 . –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –±—Г–і–µ—В
. –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –±—Г–і–µ—В
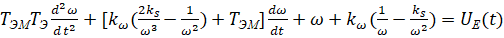 (11)
(11)
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ —Г—А–∞–≤–љ–µ–љ–Є—П (9), (11) –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ –Њ—В–ї–Є—З–∞–µ—В—Б—П –Њ—В —Г—А–∞–≤–љ–µ–љ–Є—П –і–≤–Є–≥–∞—В–µ–ї—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–≥–Њ —В–Њ–Ї–∞ [12,13], –њ—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ, –љ–∞–ї–Є—З–Є–µ–Љ –љ–µ–ї–Є–љ–µ–є–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤.
3. –С–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј —Б–Є—Б—В–µ–Љ—Л –Є —А–µ–Ј—Г–ї—М—В–∞—В—Л –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П
–°–љ–∞—З–∞–ї–∞ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–≤–Њ–є—Б—В–≤–∞ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л (9). –†–∞–≤–љ–Њ–≤–µ—Б–Є–µ —Б–Є—Б—В–µ–Љ—Л –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Є—Б—Е–Њ–і—П –Є–Ј —Г—Б–ї–Њ–≤–Є—П: —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –љ–µ–Є–Ј–Љ–µ–љ–љ–∞, —В–Њ–≥–і–∞ —В–Њ—З–Ї–∞ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є—П
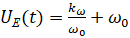 (10)
(10)
–Я—Г—Б—В—М –љ–∞–њ—А—П–ґ–µ–љ–Є–µ, –њ—А–Є–≤–µ–і—С–љ–љ–Њ–µ –Ї —З–∞—Б—В–Њ—В–µ –≤—А–∞—Й–µ–љ–Є—П –і–≤–Є–≥–∞—В–µ–ї—П, –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П, —В–Њ –µ—Б—В—М 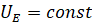 . –Х–Љ—Г —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —Б–ї–µ–і—Г—О—Й–Є–µ –Ј–љ–∞—З–µ–љ–Є—П —З–∞—Б—В–Њ—В—Л –≤—А–∞—Й–µ–љ–Є—П –і–≤–Є–≥–∞—В–µ–ї—П (—А–Є—Б. 3)
. –Х–Љ—Г —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —Б–ї–µ–і—Г—О—Й–Є–µ –Ј–љ–∞—З–µ–љ–Є—П —З–∞—Б—В–Њ—В—Л –≤—А–∞—Й–µ–љ–Є—П –і–≤–Є–≥–∞—В–µ–ї—П (—А–Є—Б. 3)
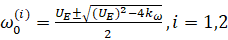 (11)
(11)
–Я—А–Є 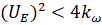 –љ–µ —Б—Г—Й–µ—Б—В–≤—Г–µ—В —Г–њ—А–∞–≤–ї–µ–љ–Є—П, –Ї–Њ—В–Њ—А–Њ–Љ—Г —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В –≤–µ—Й–µ—Б—В–≤–µ–љ–љ—Л–µ —З–∞—Б—В–Њ—В—Л –≤—А–∞—Й–µ–љ–Є—П —А–Њ—В–Њ—А–∞. –Я—А–Є
–љ–µ —Б—Г—Й–µ—Б—В–≤—Г–µ—В —Г–њ—А–∞–≤–ї–µ–љ–Є—П, –Ї–Њ—В–Њ—А–Њ–Љ—Г —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В –≤–µ—Й–µ—Б—В–≤–µ–љ–љ—Л–µ —З–∞—Б—В–Њ—В—Л –≤—А–∞—Й–µ–љ–Є—П —А–Њ—В–Њ—А–∞. –Я—А–Є 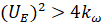 –Њ–і–љ–Њ–Љ—Г –Є —В–Њ–Љ—Г –ґ–µ –Ј–љ–∞—З–µ–љ–Є—О –љ–∞–њ—А—П–ґ–µ–љ–Є—П –љ–∞ —П–Ї–Њ—А–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О –і–≤–µ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П. –Э–µ —В—А—Г–і–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –≤–µ—А—Е–љ—П—П –≤–µ—В–≤—М —Б–Љ–µ—Й–µ–љ–Є—П —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В —Г—Б—В–Њ–є—З–Є–≤—Л–Љ —В–Њ—З–Ї–∞–Љ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П (–љ–∞–њ—А–Є–Љ–µ—А, —З–∞—Б—В–Њ—В–∞
–Њ–і–љ–Њ–Љ—Г –Є —В–Њ–Љ—Г –ґ–µ –Ј–љ–∞—З–µ–љ–Є—О –љ–∞–њ—А—П–ґ–µ–љ–Є—П –љ–∞ —П–Ї–Њ—А–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О –і–≤–µ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П. –Э–µ —В—А—Г–і–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –≤–µ—А—Е–љ—П—П –≤–µ—В–≤—М —Б–Љ–µ—Й–µ–љ–Є—П —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В —Г—Б—В–Њ–є—З–Є–≤—Л–Љ —В–Њ—З–Ї–∞–Љ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П (–љ–∞–њ—А–Є–Љ–µ—А, —З–∞—Б—В–Њ—В–∞ 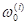 –љ–∞ —А–Є—Б. 3). –Э–Є–ґ–љ—П—П –≤–µ—В–≤—М вАУ –љ–µ—Г—Б—В–Њ–є—З–Є–≤—Л–Љ (–љ–∞–њ—А–Є–Љ–µ—А, —З–∞—Б—В–Њ—В–∞
–љ–∞ —А–Є—Б. 3). –Э–Є–ґ–љ—П—П –≤–µ—В–≤—М вАУ –љ–µ—Г—Б—В–Њ–є—З–Є–≤—Л–Љ (–љ–∞–њ—А–Є–Љ–µ—А, —З–∞—Б—В–Њ—В–∞ 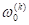 –љ–∞ —А–Є—Б. 3).
–љ–∞ —А–Є—Б. 3).
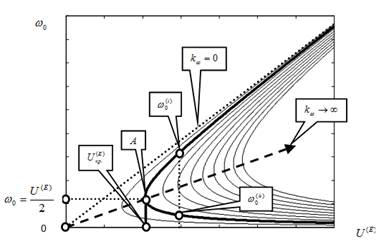
–†–Є—Б. 3. –Ф–Є–∞–≥—А–∞–Љ–Љ—Л —Б–Љ–µ—Й–µ–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –њ—А–Є —А–∞–Ј–ї–Є—З–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ 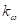
–Ф–ї—П –∞–љ–∞–ї–Є–Ј–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є —Б–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–Є–Є –Ы—П–њ—Г–љ–Њ–≤–∞ [14,15] –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ –≤ –≤–∞—А–Є–∞—Ж–Є—П—Е –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–Є—Б—В–µ–Љ—Г (9) –≤ –≤–∞—А–Є–∞—Ж–Є—П—Е –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –њ–Њ—Б–ї–µ –Ј–∞–Љ–µ–љ—Л 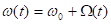 –Є –њ—А–Є–Љ–µ–Љ –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ
–Є –њ—А–Є–Љ–µ–Љ –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ  . –Ґ–Њ–≥–і–∞
. –Ґ–Њ–≥–і–∞
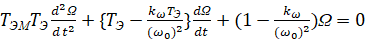 (12)
(12)
–Я–Њ—В–µ—А—П —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Ј–∞–≤–Є—Б–Є—В –Њ—В –Ј–љ–∞–Ї–∞ —Н–ї–µ–Љ–µ–љ—В–∞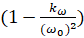 . –Я–Њ—Н—В–Њ–Љ—Г –љ–∞ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л—Е –і–≤—Г—Е –≤–µ—В–≤—П—Е —В—А–∞–µ–Ї—В–Њ—А–Є–Є —Б–Љ–µ—Й–µ–љ–Є—П —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б —Г—Б–ї–Њ–≤–Є–µ–Љ
. –Я–Њ—Н—В–Њ–Љ—Г –љ–∞ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л—Е –і–≤—Г—Е –≤–µ—В–≤—П—Е —В—А–∞–µ–Ї—В–Њ—А–Є–Є —Б–Љ–µ—Й–µ–љ–Є—П —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б —Г—Б–ї–Њ–≤–Є–µ–Љ 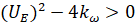 . –Я–Њ—Н—В–Њ–Љ—Г
. –Я–Њ—Н—В–Њ–Љ—Г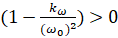 –њ—А–Є —Г—Б–ї–Њ–≤–Є–Є
–њ—А–Є —Г—Б–ї–Њ–≤–Є–Є 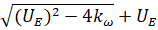 , —З—В–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –≤–µ—А—Е–љ–µ–є –≤–µ—В–≤–Є —В—А–∞–µ–Ї—В–Њ—А–Є–Є (—А–Є—Б. 3). –Х—Б–ї–Є
, —З—В–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –≤–µ—А—Е–љ–µ–є –≤–µ—В–≤–Є —В—А–∞–µ–Ї—В–Њ—А–Є–Є (—А–Є—Б. 3). –Х—Б–ї–Є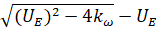 , —З—В–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –љ–Є–ґ–љ–µ–є –≤–µ—В–≤–Є, —В–Њ
, —З—В–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –љ–Є–ґ–љ–µ–є –≤–µ—В–≤–Є, —В–Њ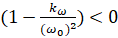 . –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ–Є–ґ–љ—П—П –≤–µ—В–≤—М —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–Љ—Г —А–∞–≤–љ–Њ–≤–µ—Б–Є—О.
. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ–Є–ґ–љ—П—П –≤–µ—В–≤—М —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–Љ—Г —А–∞–≤–љ–Њ–≤–µ—Б–Є—О.
–Я—А–Є–≤–µ–і—С–Љ –њ—А–Є–Љ–µ—А —Д–∞–Ј–Њ–≤–Њ–≥–Њ –њ–Њ—А—В—А–µ—В–∞ —Б–Є—Б—В–µ–Љ—Л –і–ї—П –і–≤–Є–≥–∞—В–µ–ї—П, –Є–Љ–µ—О—Й–µ–≥–Њ —Б–ї–µ–і—Г—О—Й–Є–µ –њ–∞—А–∞–Љ–µ—В—А—Л: 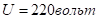 ,
,  ,
, 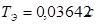 ,
, 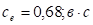 ,
, 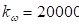 (—А–Є—Б. 4).
(—А–Є—Б. 4).
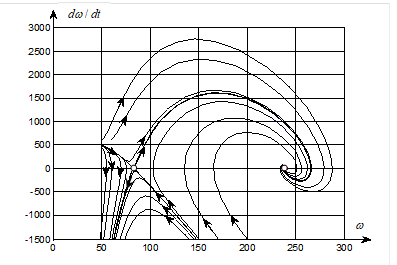
–†–Є—Б. 4. –§–∞–Ј–Њ–≤–Њ–є –њ–Њ—В—А–µ—В —Б–Є—Б—В–µ–Љ—Л
–Ъ–∞–Ї –≤–Є–і–љ–Њ, —Б–Є—Б—В–µ–Љ–∞ –Є–Љ–µ–µ—В –і–≤–µ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П: (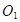 ) –Є (
) –Є (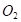 ). –Я–µ—А–≤–∞—П —В–Њ—З–Ї–∞
). –Я–µ—А–≤–∞—П —В–Њ—З–Ї–∞ 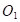 —П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є. –Т—В–Њ—А–∞—П —В–Њ—З–Ї–∞
—П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є. –Т—В–Њ—А–∞—П —В–Њ—З–Ї–∞ 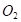 -—Г—Б—В–Њ–є—З–Є–≤–∞. –≠—В–Є —В–Њ—З–Ї–Є —Д–Њ—А–Љ–Є—А—Г—О—В –і–≤–µ –Њ–±–ї–∞—Б—В–Є, —А–∞–Ј–і–µ–ї—С–љ–љ—Л–µ —Б–µ–њ–∞—А–∞—В—А–Є—Б—Б–љ–Њ–є –Ї—А–Є–≤–Њ–є. –Я—А–Є—З–µ–Љ, –Њ–і–љ–∞ –≤–µ—В–≤—М —Б–µ–њ–∞—А–∞—В—А–Є—Б—Б—Л —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В –∞—В—В—А–∞–Ї—В–Њ—А, –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–Є–є—Б—П –Ї —В–Њ—З–Ї–µ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П
-—Г—Б—В–Њ–є—З–Є–≤–∞. –≠—В–Є —В–Њ—З–Ї–Є —Д–Њ—А–Љ–Є—А—Г—О—В –і–≤–µ –Њ–±–ї–∞—Б—В–Є, —А–∞–Ј–і–µ–ї—С–љ–љ—Л–µ —Б–µ–њ–∞—А–∞—В—А–Є—Б—Б–љ–Њ–є –Ї—А–Є–≤–Њ–є. –Я—А–Є—З–µ–Љ, –Њ–і–љ–∞ –≤–µ—В–≤—М —Б–µ–њ–∞—А–∞—В—А–Є—Б—Б—Л —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В –∞—В—В—А–∞–Ї—В–Њ—А, –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–Є–є—Б—П –Ї —В–Њ—З–Ї–µ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П 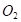 .
.
–Ґ–µ–њ–µ—А—М —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –±–Є—Д—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ—Л–µ —Б–≤–Њ–є—Б—В–≤–∞ —Б–Є—Б—В–µ–Љ—Л (11). –Я—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ, —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л (11) –і–ї—П –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –і–≤–Є–≥–∞—В–µ–ї—П 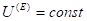 . –Ф–ї—П –њ–Њ—П—Б–љ–µ–љ–Є—П –≤–ї–Є—П–љ–Є—П —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л —Г–і–Њ–±–љ–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –≥—А–∞—Д–Є—З–µ—Б–Ї–Њ–є –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–µ–є —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П (—А–Є—Б. 5). –£—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П
. –Ф–ї—П –њ–Њ—П—Б–љ–µ–љ–Є—П –≤–ї–Є—П–љ–Є—П —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л —Г–і–Њ–±–љ–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –≥—А–∞—Д–Є—З–µ—Б–Ї–Њ–є –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–µ–є —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П (—А–Є—Б. 5). –£—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П 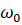 –±—Г–і–µ—В
–±—Г–і–µ—В
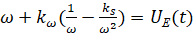 (13)
(13)
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ —Б–≤–Њ–є—Б—В–≤–∞ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–Љ 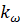 . –Я—А–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–µ
. –Я—А–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–µ 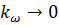 —Б–≤–Њ–є—Б—В–≤–Њ –і–≤–Є–≥–∞—В–µ–ї—П –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —В—А–∞–і–Є—Ж–Є–Њ–љ–љ–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М—О —З–∞—Б—В–Њ—В—Л —П–Ї–Њ—А—П –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П
—Б–≤–Њ–є—Б—В–≤–Њ –і–≤–Є–≥–∞—В–µ–ї—П –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —В—А–∞–і–Є—Ж–Є–Њ–љ–љ–Њ–є –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М—О —З–∞—Б—В–Њ—В—Л —П–Ї–Њ—А—П –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П 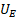 . –Т —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В
. –Т —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В 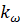 –Ј–∞–≤–Є—Б–Є—В –Њ—В –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–Њ—Й–љ–Њ—Б—В–Є –і–≤–Є–≥–∞—В–µ–ї—П –Ї –Љ–Њ—Й–љ–Њ—Б—В–Є –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –µ—Б–ї–Є –Љ–Њ—Й–љ–Њ—Б—В—М –і–≤–Є–≥–∞—В–µ–ї—П –љ–µ–Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В, —В–Њ —А–µ–∞–Ї—Ж–Є—П —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –љ–Є–≤–µ–ї–Є—А—Г–µ—В—Б—П. –Т —В–Њ–Љ –ґ–µ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ –Љ–Њ—Й–љ–Њ—Б—В—М –і–≤–Є–≥–∞—В–µ–ї—П –Є –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П —Б–Њ–Є–Ј–Љ–µ—А–Є–Љ—Л, —В–Њ –≤ –Њ–±–ї–∞—Б—В–Є –Љ–∞–ї—Л—Е —З–∞—Б—В–Њ—В –≤—А–∞—Й–µ–љ–Є—П
–Ј–∞–≤–Є—Б–Є—В –Њ—В –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–Њ—Й–љ–Њ—Б—В–Є –і–≤–Є–≥–∞—В–µ–ї—П –Ї –Љ–Њ—Й–љ–Њ—Б—В–Є –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –µ—Б–ї–Є –Љ–Њ—Й–љ–Њ—Б—В—М –і–≤–Є–≥–∞—В–µ–ї—П –љ–µ–Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В, —В–Њ —А–µ–∞–Ї—Ж–Є—П —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –љ–Є–≤–µ–ї–Є—А—Г–µ—В—Б—П. –Т —В–Њ–Љ –ґ–µ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ –Љ–Њ—Й–љ–Њ—Б—В—М –і–≤–Є–≥–∞—В–µ–ї—П –Є –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П —Б–Њ–Є–Ј–Љ–µ—А–Є–Љ—Л, —В–Њ –≤ –Њ–±–ї–∞—Б—В–Є –Љ–∞–ї—Л—Е —З–∞—Б—В–Њ—В –≤—А–∞—Й–µ–љ–Є—П
–і–≤–Є–≥–∞—В–µ–ї—П —Д–Њ—А–Љ–Є—А—Г–µ—В—Б—П –Њ–±–ї–∞—Б—В—М –љ–µ–Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ—Б—В–Є –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —З–∞—Б—В–Њ—В—Л –≤—А–∞—Й–µ–љ–Є—П –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П. –Я—А–Є —Н—В–Њ–Љ –њ–Њ –Љ–µ—А–µ —Г–≤–µ–ї–Є—З–µ–љ–Є—П –љ–∞–њ—А—П–ґ–µ–љ–Є—П –Є–Љ–µ—О—В –Љ–µ—Б—В–Њ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Є —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —В–Є–њ–∞ –≤–Є–ї–Ї–Є. –Э–∞–њ—А–Є–Љ–µ—А, –і–ї—П –љ–∞–њ—А—П–ґ–µ–љ–Є—П 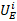 —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —В—А–Є —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П: ¬Ђ1¬ї, ¬Ђ2¬ї –Є ¬Ђ3¬ї. –Я—А–Є—З–µ–Љ —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–µ —В–Њ—З–Ї–µ ¬Ђ2¬ї, —П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤—Л–Љ. –Э–µ—Г—Б—В–Њ–є—З–Є–≤—Л–Љ–Є —П–≤–ї—П—О—В—Б—П –≤—Б–µ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –љ–∞—Е–Њ–і—П—Й–Є–µ—Б—П –љ–∞ –Ї—А–Є–≤–Њ–є ¬Ђ–Т-D¬ї. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ—А–Є –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є–Є –љ–∞–њ—А—П–ґ–µ–љ–Є—П —В—А–∞–µ–Ї—В–Њ—А–Є—П —Б–Љ–µ—Й–µ–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Ї—А–Є–≤–Њ–є ¬Ђ–Р-–Т-–°¬ї, –њ—А–Є —Г–Љ–µ–љ—М—И–µ–љ–Є–Є вАУ –Ї—А–Є–≤–Њ–є ¬Ђ–°-D-–Р¬ї.
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —В—А–Є —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П: ¬Ђ1¬ї, ¬Ђ2¬ї –Є ¬Ђ3¬ї. –Я—А–Є—З–µ–Љ —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–µ —В–Њ—З–Ї–µ ¬Ђ2¬ї, —П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤—Л–Љ. –Э–µ—Г—Б—В–Њ–є—З–Є–≤—Л–Љ–Є —П–≤–ї—П—О—В—Б—П –≤—Б–µ —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –љ–∞—Е–Њ–і—П—Й–Є–µ—Б—П –љ–∞ –Ї—А–Є–≤–Њ–є ¬Ђ–Т-D¬ї. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ—А–Є –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є–Є –љ–∞–њ—А—П–ґ–µ–љ–Є—П —В—А–∞–µ–Ї—В–Њ—А–Є—П —Б–Љ–µ—Й–µ–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Ї—А–Є–≤–Њ–є ¬Ђ–Р-–Т-–°¬ї, –њ—А–Є —Г–Љ–µ–љ—М—И–µ–љ–Є–Є вАУ –Ї—А–Є–≤–Њ–є ¬Ђ–°-D-–Р¬ї.
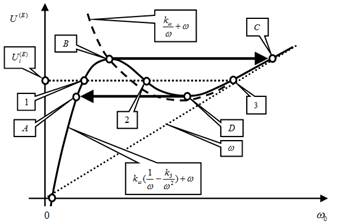
–†–Є—Б. 5. –Ф–Є–∞–≥—А–∞–Љ–Љ—Л —Б–Љ–µ—Й–µ–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П
–Ф–ї—П —Н—В–Њ–≥–Њ —Б–ї—Г—З–∞—П –њ—А–Є–≤–µ–і—С–Љ –њ—А–Є–Љ–µ—А —Д–∞–Ј–Њ–≤–Њ–≥–Њ –њ–Њ—А—В—А–µ—В–∞ —Б–Є—Б—В–µ–Љ—Л (—А–Є—Б. 6). –С–ї–Њ–Ї —Б—Е–µ–Љ–∞ –Є –њ—А–Њ–≥—А–∞–Љ–Љ–∞ –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П —Д–∞–Ј–Њ–≤–Њ–є —В—А–∞–µ–Ї—В–Њ—А–Є–Є —В–∞–Ї–ґ–µ –њ—А–Є–≤–µ–і–µ–љ–∞ –≤ –њ—А–Є–ї–Њ–ґ–µ–љ–Є–Є. –Ч–і–µ—Б—М –Є–Љ–µ–µ—В—Б—П —В—А–Є —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П 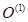 ,
, 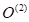 –Є
–Є  . –Я—А–Є—З–µ–Љ, —В–Њ—З–Ї–∞
. –Я—А–Є—З–µ–Љ, —В–Њ—З–Ї–∞  —П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є. –Ш–Ј —Н—В–Њ–є —В–Њ—З–Ї–Є –≤—Л—Е–Њ–і—П—В —Б–µ–њ–∞—А–∞—В—А–Є—Б—Б–љ—Л–µ –Ї—А–Є–≤—Л–µ, –Ї–Њ—В–Њ—А—Л–µ –і–µ–ї—П—В —Д–∞–Ј–Њ–≤–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –љ–∞ –і–≤–µ –Њ–±–ї–∞—Б—В–Є –њ—А–Є—В—П–ґ–µ–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П
—П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є. –Ш–Ј —Н—В–Њ–є —В–Њ—З–Ї–Є –≤—Л—Е–Њ–і—П—В —Б–µ–њ–∞—А–∞—В—А–Є—Б—Б–љ—Л–µ –Ї—А–Є–≤—Л–µ, –Ї–Њ—В–Њ—А—Л–µ –і–µ–ї—П—В —Д–∞–Ј–Њ–≤–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –љ–∞ –і–≤–µ –Њ–±–ї–∞—Б—В–Є –њ—А–Є—В—П–ґ–µ–љ–Є—П —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П 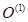 –Є
–Є  .
.
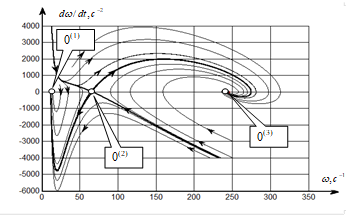
–†–Є—Б.6 –§–∞–Ј–Њ–≤–Њ–є –њ–Њ—В—А–µ—В –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П —Б –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П
–Я—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А—Г–µ–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В.
1. –Ф–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є –Ј–∞ —Б—З—С—В —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –Љ–Њ–≥—Г—В —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –Љ–µ–љ—П—В—М —Б–≤–Њ–Є —Б–≤–Њ–є—Б—В–≤–∞.
2. –Т–ї–Є—П–љ–Є–µ –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –љ–∞ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ –њ—А–Є–≤–Њ–і–∞ –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –Ј–∞–≤–Є—Б–Є—В, –Ї–∞–Ї –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П, —В–∞–Ї –Є –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –і–≤–Є–≥–∞—В–µ–ї—П. –•–∞—А–∞–Ї—В–µ—А–љ–Њ, —З—В–Њ –њ–Њ –Љ–µ—А–µ —Г–Љ–µ–љ—М—И–µ–љ–Є—П –Љ–Њ—Й–љ–Њ—Б—В–Є —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї—П –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Љ–Њ—Й–љ–Њ—Б—В—М—О –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –њ—А–Њ—П–≤–ї–µ–љ–Є–µ –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В–Є —Б–≤–Њ–є—Б—В–≤ –і–≤–Є–≥–∞—В–µ–ї—П –≤–Њ–Ј—А–∞—Б—В–∞–µ—В. –Ъ—А–Њ–Љ–µ —Н—В–Њ–≥–Њ, –і–ї—П –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є —Г—Б—В–Њ–є—З–Є–≤–Њ–є —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б—Г—Й–µ—Б—В–≤—Г–µ—В –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–∞—П –Њ–±–ї–∞—Б—В—М –њ—А–Є—В—П–ґ–µ–љ–Є—П.
3. –° –њ–µ—А–≤–Њ–≥–Њ –≤–Ј–≥–ї—П–і–∞, —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П–Љ –Њ —Б–≤–Њ–є—Б—В–≤–∞—Е —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є. –Ю–і–љ–∞–Ї–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Г—З–Є—В—Л–≤–∞—В—М, —З—В–Њ –њ–Њ –Љ–µ—А–µ —Г–Љ–µ–љ—М—И–µ–љ–Є—П —Б–Ї–Њ—А–Њ—Б—В–Є —А–µ–Ј–∞–љ–Є—П –њ—А–Є –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –њ–Њ–і–∞—З–Є —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В –њ–ї–Њ—Й–∞–і—М —Б—А–µ–Ј–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П. –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –љ–µ–њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ –±—Л—Б—В—А–Њ —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П –Љ–Њ–Љ–µ–љ—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П, –Ї–Њ—В–Њ—А—Л–є –њ—А–Є –љ–µ–і–Њ—Б—В–∞—В–Њ—З–љ–Њ–є –Љ–Њ—Й–љ–Њ—Б—В–Є –і–≤–Є–≥–∞—В–µ–ї—П –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П –Љ–Њ–ґ–µ—В –њ—А–µ–≤—Л—И–∞—В—М –Љ–Њ–Љ–µ–љ—В –і–≤–Є–≥–∞—В–µ–ї—П. –≠—В–Њ –Њ–і–Є–љ –Є–Ј –Љ–µ—Е–∞–љ–Є–Ј–Љ–Њ–≤ —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П –Ј–∞–Ї–ї–Є–љ–Є–≤–∞–љ–Є—П —А–µ–ґ—Г—Й–µ–≥–Њ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞.
–Я—А–Є–≤–µ–і—С–љ–љ—Л–є –Љ–∞—В–µ—А–Є–∞–ї –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –і–ї—П —Б–Є—Б—В–µ–Љ—Л –і–Є–љ–∞–Љ–Є–Ї–Є –њ—А–Є–≤–Њ–і–∞ –Є—Б–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Г—З–Є—В—Л–≤–∞—В—М —А–µ–∞–Ї—Ж–Є—О —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П. –Ф–ї—П –Њ–±–µ—Б–њ–µ—З–µ–љ–Є—П —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є —Б–Є—Б—В–µ–Љ—Л –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–Њ–≥–ї–∞—Б–Њ–≤—Л–≤–∞—В—М –њ–∞—А–∞–Љ–µ—В—А—Л –і–≤–Є–≥–∞—В–µ–ї—П —Б–Њ —Б–≤–Њ–є—Б—В–≤–∞–Љ–Є –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–≤—П–Ј–Є, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–є –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П.
–Ч–∞–Ї–ї—О—З–µ–љ–Є–µ
–Ч–∞ —Б—З—С—В —А–µ–∞–Ї—Ж–Є–Є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –Є–Ј–Љ–µ–љ—П—О—В—Б—П –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є –Є—Б–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —Б—В–∞–љ–Ї–∞. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —А–µ–∞–Ї—Ж–Є—П —Б–Њ —Б—В–Њ—А–Њ–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞ —А–µ–Ј–∞–љ–Є—П –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В—Б—П –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —Б–Њ—Б—В–Њ—П–љ–Є—П —Б–Є—Б—В–µ–Љ—Л. –Э–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є—Е —Б–≤–Њ–є—Б—В–≤ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ–µ –≤–ї–Є—П–љ–Є–µ –Њ–Ї–∞–Ј—Л–≤–∞–µ—В —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–Њ–Љ–Є–љ–∞–ї—М–љ–Њ–є –Љ–Њ—Й–љ–Њ—Б—В–Є –і–≤–Є–≥–∞—В–µ–ї–µ–є –Є –Љ–Њ—Й–љ–Њ—Б—В–Є –њ—А–Њ—Ж–µ—Б—Б–∞ –Њ–±—А–∞–±–Њ—В–Ї–Є. –Х—Б–ї–Є –Љ–Њ—Й–љ–Њ—Б—В—М –і–≤–Є–≥–∞—В–µ–ї—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –±–Њ–ї—М—И–µ –Љ–Њ—Й–љ–Њ—Б—В–Є —А–µ–Ј–∞–љ–Є—П, —В–Њ —А–µ–∞–Ї—Ж–Є–µ–є —Б–Њ —Б—В–Њ—А–Њ–љ—Л –Њ–±—А–∞–±–Њ—В–Ї–Є –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М. –Т –њ—А–Њ—В–Є–≤–љ–Њ–Љ —Б–ї—Г—З–∞–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞, –љ–∞–њ—А–Є–Љ–µ—А, –≤—А–∞—Й–µ–љ–Є—П —И–њ–Є–љ–і–µ–ї—П, —Б—В–∞–љ–Њ–≤–Є—В—Б—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –љ–µ–ї–Є–љ–µ–є–љ–Њ–є. –Я—А–Є –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л—Е —А–µ–ґ–Є–Љ–∞—Е –љ–µ–ї–Є–љ–µ–є–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї—Г—О —Б–≤—П–Ј—М, —П–≤–ї—П—О—В—Б—П –љ–µ–Њ–і–љ–Њ–Ј–љ–∞—З–љ—Л–Љ–Є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞—О—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–µ –љ–µ –Є–Ј–≤–µ—Б—В–љ—Л–µ —А–∞–љ–µ–µ –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В–Є —Б–Є—Б—В–µ–Љ—Л: –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –і–≤–Є–≥–∞—В–µ–ї—П –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ —В—А–µ—Е —В–Њ—З–µ–Ї —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –Њ–і–љ–∞ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е —П–≤–ї—П–µ—В—Б—П –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–є; –њ–Њ –Љ–µ—А–µ —Г–≤–µ–ї–Є—З–µ–љ–Є—П –љ–∞–њ—А—П–ґ–µ–љ–Є—П —П–Ї–Њ—А—П –љ–∞–±–ї—О–і–∞–µ—В—Б—П –±–Є—Д—Г—А–Ї–∞—Ж–Є—П —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Б–Є—Б—В–µ–Љ—Л —В–Є–њ–∞ –≤–Є–ї–Ї–Є, —В–Њ—З–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Њ–±–ї–∞–і–∞—О—В –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–є –Њ–±–ї–∞—Б—В—М—О –њ—А–Є—В—П–ґ–µ–љ–Є—П. –Ґ–∞–Ї –Ї–∞–Ї –њ–∞—А–∞–Љ–µ—В—А—Л –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–≤—П–Ј–Є, —Д–Њ—А–Љ–Є—А—Г–µ–Љ–Њ–є –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ —А–µ–Ј–∞–љ–Є—П, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—В—Б—П —Б–≤–Њ–є—Б—В–≤–Њ–Љ —Н–≤–Њ–ї—О—Ж–Є–Њ–љ–љ–Њ–є –Є–Ј–Љ–µ–љ—З–Є–≤–Њ—Б—В–Є, —В–Њ –≤ –њ—А–Њ—Ж–µ—Б—Б–µ —А–µ–Ј–∞–љ–Є—П –Є–Ј–Љ–µ–љ—П—О—В—Б—П –Є —Б–≤–Њ–є—Б—В–≤–∞ —Б–µ—А–≤–Њ–і–≤–Є–≥–∞—В–µ–ї–µ–є.
–Ы–Є—В–µ—А–∞—В—Г—А–∞
1. Addasi, E.S. (2013) вАШModelling and simulation of DC motor electric drive control system with variable moment of inertiaвАЩ, ACEEE Int. J. on Electrical and Power Engineering, Vol. 4, No. 1, pp.52вАУ57.
2. Canniere, J.D., Brussel, H.V. and Bogaert, J. (1981) вАШA contribution to the mathematical analysis of variable spindle speed machiningвАЩ, Applied Mathematical Modelling, Vol. 5, No. 3, pp.158вАУ164.
3. Cao, H., Li, B. and He, Z. (2012) вАШChatter stability of milling with speed varying dynamic of spindlesвАЩ, International Journal of Machine Tools & Manufacture, Vol. 52, No. 1, pp.50вАУ58.
3. DвАЩMello, G., Pai, P.S., Puneet, N.P. and Fang, N. (2016) вАШSurface roughness evaluation using cutting vibrations in high speed turning of Ti-6Al-4V вАУ an experimental approachвАЩ, International Journal of Machining and Machinability of Materials, Vol. 18, No. 3, pp.288вАУ312.
4. Dombovari, Z., Wilson, R.E. and Stepan, G. (2008) вАШOn the robustness of stable turning processesвАЩ, International Journal of Machining and Machinability of Materials, Vol. 4, No.4, pp.320вАУ334.
5. Gagnol, V., Belhassen, C. Bouzgarrou, P.R. and Barra, C. (2006) вАШStability based spindle design optimizationвАЩ, Journal of Manufacturing Science and Engineering, Vol. 129, No. 2, pp.407вАУ415.
6. Jayaram, S., Kapoor, S.G. and DeVor, R.E. (2000) вАШAnalytical stability analysis of variable spindle speed machiningвАЩ, Journal of Manufacturing Science and Engineering, Vol. 122, No. 3, pp.391вАУ397.
7. Jemielniak, K. and Windota, A. (1984) вАШSuppression of self-excited vibration by the spindle speed variation methodвАЩ, International Journal of Machine Tool Design and Research, Vol. 24,No. 3, pp.207вАУ214.
8. Dynamical analysis for the motorised spindles of machine tools
Xie, Q., Zhang, Q. and Han, J. (2012) вАШHopf bifurcation for delay differential equation with application to machine tool chatterвАЩ, Applied Mathematical Modelling, Vol. 36, No. 8, pp.3803вАУ3812.
9. HuihuiMiao at al, Dynamic analysis of the column-spindle system considering the nonlinear characteristics of kinematic joints, Mechanism and Machine Theory, Volume 174, August 2022, 104922
10. Juan Xu at al, Vibration characteristics of unbalance response for motorized spindle system, Procedia Engineering 174 (2017) 331 вАУ 340.
11. –Ч–∞–Ї–Њ–≤–Њ—А–Њ—В–љ—Л–є –Т.–Ы., –Ы—Г–Ї—М—П–љ–Њ–≤ –Р.–Ф., –Э–≥—Г–µ–љ –Ф–Њ–љ–≥ –Р–љ—М, –§–∞–Љ –Ф–Є–љ—М –Ґ—Г–љ–≥. –°–Є–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Є–є —Б–Є—Б—В–µ–Љ–љ—Л–є —Б–Є–љ—В–µ–Ј —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ–є –і–Є–љ–∞–Љ–Є–Ї–Є –Љ–µ—В–∞–ї–ї–Њ—А–µ–ґ—Г—Й–Є—Е —Б—В–∞–љ–Ї–Њ–≤ —Б —Г—З–µ—В–Њ–Љ —Н–≤–Њ–ї—О—Ж–Є–Є —Б–≤—П–Ј–µ–є. –†–Њ—Б—В–Њ–≤ –љ/–Ф: –Ш–Ј–і–∞—В–µ–ї—М—Б–Ї–Є–є —Ж–µ–љ—В—А –Ф–У–Ґ–£, 2008. вАУ 324 —Б.
12. –Ч–∞–Ї–Њ–≤–Њ—А–Њ—В–љ—Л–є –Т.–Ы., –°–µ–Љ–Ї–Њ –Ш.–Р. –≠–ї–µ–Ї—В—А–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–µ —Б–Є—Б—В–µ–Љ—Л. –†–Њ—Б—В–Њ–≤ –љ/–Ф: –Ш–Ј–і–∞—В–µ–ї—М—Б–Ї–Є–є —Ж–µ–љ—В—А –Ф–У–Ґ–£. 2000.- 213 —Б.
13. –Ш–≤–∞–љ–Њ–≤ вАУ –°–Љ–Њ–ї–µ–љ—Б–Ї–Є–є –Т.–Р. –≠–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–Є–µ –Љ–∞—И–Є–љ—Л. –Ь.: –Є–Ј–і-–≤–Њ ¬Ђ–≠–љ–µ—А–≥–Є—П¬ї. 1980.- 928 —Б.
13. –Р—Д–∞–љ–∞—Б—М–µ–≤ –Т.–Э., –Ъ–Њ–ї–Љ–∞–љ–Њ–≤—Б–Ї–Є–є –Т.–С., –Э–Њ—Б–Њ–≤ –Т.–†. –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П —В–µ–Њ—А–Є—П –Ї–Њ–љ—Б—В—А—Г–Є—А–Њ–≤–∞–љ–Є—П —Б–Є—Б—В–µ–Љ —Г–њ—А–∞–≤–ї–µ–љ–Є—П. –Ь.: –Т—Л—Б—И–∞—П —И–Ї–Њ–ї–∞, 1989 -447 —Б.
14. –Ъ–Є–Љ –Ф.–Я. –Ґ–µ–Њ—А–Є—П –∞–≤—В–Њ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Г–њ—А–∞–≤–ї–µ–љ–Є—П. –Ы–Є–љ–µ–є–љ—Л–µ —Б–Є—Б—В–µ–Љ—Л. –Ь.: –§–Є–Ј–Љ–∞—В–ї–Є—В, 2007.- 312 —Б.









