Теоретический анализ работы модернизированного картофелекопателя

Ключевые слова: картофелеуборочная машина, модернизированный картофелекопатель, колеблющейся лемех, закон движения лемеха, закон движения частицы почвы.

В статье приведены теоретические исследования работы активного лемеха. Рассмотрена динамика лемеха и частицы почвы, находящейся на поверхности лемеха. Получены законы движения самоколеблющегося лемеха и частицы почвы.

Theoretical analysis of work of the modernized potato digger

Keywords: potato digger, modernization potato digger, the fluctuating ploughshare, the law of the movement of a ploughshare, the law of the movement of a particle of the soil

Theoretical researches of work of an active ploughshare are given in article. Fluctuations of a ploughshare and the particle of soil, which is located on the surface of a ploughshare, are considered. The obtained laws of motion of a vibrating plow and particle of soil

Подкапывающие рабочие органы картофелеуборочных машин выполняют начальную операцию в технологическом процессе работы картофелеуборочной машины. Широкое распространение получили пассивные лемеха, которые применяются на картофелекопателях. Но они имеют недостатки: часто происходит сгруживание почвенного пласта из-за неудовлетворительного продвижения по поверхности лемеха, происходит зависание ботвы и растительных остатков. Поэтому был разработан картофелекопатель с самоколеблющимися лемехами [1,2].

Для исследования движения самоколеблющегося лемеха рассмотрим систему, состоящую из лемеха и частицы почвы (рисунок 1).

Рисунок 1- Силы, действующие на систему лемех - частица грунта

На систему действуют сила тяжести лемеха , сила тяжести частицы грунта , сила упругости , сила резания грунта , сила трения частицы грунта о поверхность лемеха, сила тяги картофелекопателя, нормальная реакция опорной поверхности лемеха для частицы грунта.

Для описания движения системы используем уравнения Лагранжа второго рода. Система имеет две степени свободы, поэтому в качестве обобщенных координат примем: х – перемещение лемеха и у – перемещение частицы грунта по поверхности лемеха (рисунок 2).

Рисунок 2- Схема для составления уравнения движения лемеха с частицей грунта

Тогда уравнения Лагранжа будут иметь вид [3]

(1)

Кинетическая энергия системы равна ,

где - кинетическая энергия поступательного движения лемеха; - кинетическая энергия частицы почвы.

Скорости v₁ и v₂ в обобщенных координатах имеют вид:

и .

Тогда кинетическая энергия системы будет равна

. (2)

Обобщенная сила соответствующая обобщенной координате х равна

. (3)

Обобщенная сила соответствующая обобщенной координате у равна

. (4)

Подставляя (2), (3) и (4) в (1), получим систему уравнений, описывающих движение системы лемех – частица грунта.

(5)

Из второго уравнения системы (5) найдем

, (6)

подставим в первое уравнение системы (5), и после преобразования, получим:

Обозначая и, учитывая, что сила резания имеет вид [4]

, (7)

получим для четырех гармоник дифференциальное уравнение движения лемеха

, (8)

Где

(9)

Решив полученное дифференциальное уравнение операционным методом, получим закон движения лемеха

(10)

Постоянные a, b, n и k определяются формулами (9).

Закон движения лемеха при a = 0,05 м/с², b = 100 м/с, n = 40 м^-1 и

k = 20 с^-1 показан на рисунке 4.

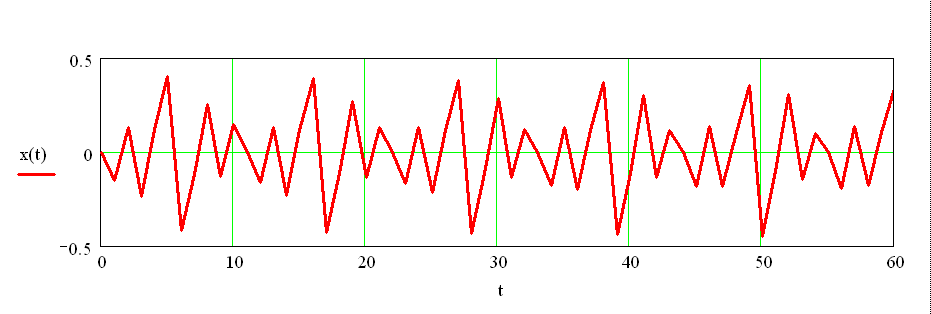
Рисунок 4 – Закон движения лемеха

Найдем закон движения частицы почвы, находящейся на поверхности лемеха. В результате интегрирования уравнения (6), получим

(11)

где х(t) – закон движения лемеха (10).

Подставляя (10) в (11), получим закон движения частицы почвы, находящейся на поверхности лемеха.

(12)

Закон движения частицы почвы при a = 0,05 м/с², b = 100 м/с, n = 40 м^-1 и k = 20 с^-1 f = 0,5 и α = 30⁰ показан на рисунке 5.

Рисунок 5 - Закон движения частицы почвы

Выводы. 1. Теоретические исследования показали, что лемех, модернизированный с помощью цилиндрической пружины, совершает колебательные движения.

2. Частица почвы, находящаяся на самоколеблющемся лемехе, подвергается вибрациям со стороны лемеха, что позволяет улучшить процесс первичной сепарации почвы.

3. Полевые испытания [5] подтверждают достоверность теоретического исследования.

Литература

1. Иванкина О.П., Угланов М.Б., Чхетиани А.А. Подпружиненный лемех картофелеуборочной машины // Проблемы механизации агрохимического обслуживания сельского хозяйства: сб. науч. тр. ГНУ ВНИМС Россельхозакадемии: - Рязань, 2013, С 159-163.

2. Иванкина О.П., Угланов М.Б., Чхетиани А.А. Теоретическое исследование движения самоколеблющегося лемеха картофелеуборочной машины// Техника и оборудование для села.. № 12, 2012, С. 8 – 10.

3.Яблонский А.А. Курс теоретической механики: учебник – 15 – е изд., стер. –М.: КНОРУС, 2010. – 608 с.

4. Иванкина О.П., Угланов М.Б., Чхетиани А.А. Теоретическое определение усилия резания усовершенствованного подкапывающего лемеха картофелекопателя // Вестник Ульяновской государственной сельскохозяйственной академии № 1, 2012, С. 143 – 144

5. Иванкина О.П., Угланов М.Б., Чхетиани А.А. Полевые испытания экспериментального картофелекопателя с самоколеблющимися лемехами. // Аграрная наука Евро – Северо – Востока. № 2 (27) 2012, С. 64-68.