Обзор нейронной сети Хемминга

Аннотация

В данной работе представлен краткий обзор нейронной сети Хемминга.

Ключевые слова

Нейрон, слой, обратная связь, классификация, образ.

Введение

Нейронные сети Хемминга можно использовать для реализации ассоциативной памяти в тех случаях, когда нет необходимости, чтобы сеть выдавала на выходе образ в явном виде, а достаточно только его номер (или код). По сравнению с сетью Хопфилда сеть Хемминга имеет меньшие затраты на память и объем требуемых вычислений.

Основная часть

Нейронная сеть Хемминга состоит из двух слоев, каждый из которых содержит число нейронов M, равное числу хранящихся образов. Нейроны первого слоя имеют N связей, соединенными со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой отрицательными обратными связями. Единственную положительную обратную связь каждый нейрон имеет с собственным выходом.

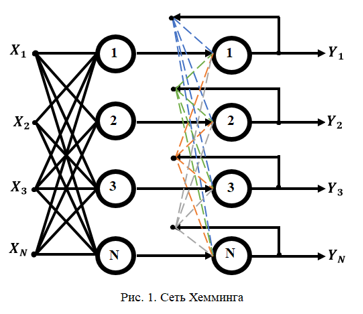
Искусственная нейронная сеть Хэмминга используется для решения задач классификации бинарных входных векторов. В основе ее работы лежат процедуры, направленные на выбор в качестве решения задачи классификации одного из эталонных образов, наиболее близкого к поданному на вход сети зашумленному входному образу, и отнесение данного образа к соответствующему классу. Для оценки меры близости к каждому классу используется критерий, учитывающий расстояние Хэмминга — количество различающихся переменных у зашумленного и эталонного входных образов.

На стадии обучения выполняется следующая последовательность действий:

2. Рассчитывается матрица весовых коэффициентов нейронов первого слоя:

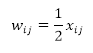
3. Определяются настройки активационной функции:

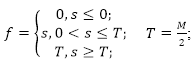
4. Задаются значения синапсов обратных связей нейронов второго слоя в виде элементов квадратной матрицы размера K x K:

5. Устанавливается максимально допустимое значение нормы разности выходных векторов на двух последовательных итерациях E_max, требующееся для оценки стабилизации решения. Обычно достаточно принимать E_max =0,1.

Для тестирования настроенной сети используем два зашумленных графических образа, показанных на рис. 2.

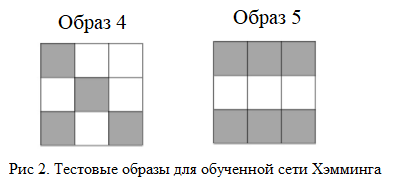
Сигналы нейронной сети Хэмминга, получаемые на протяжении полного цикла расчета при подаче тестового образа 4 на ее входы, представлены в таб.2.

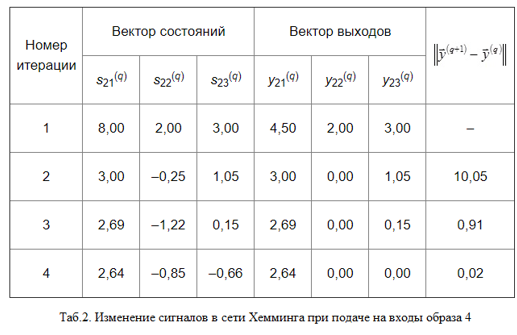
Как видно из таблицы 2, критерий остановки цикла возврата сигнала по обратным связям выполнен после 4-й итерации. Положительное выходное значение 1-го нейрона указывает на то, что зашумленный входной образ следует отнести к 1-му классу.

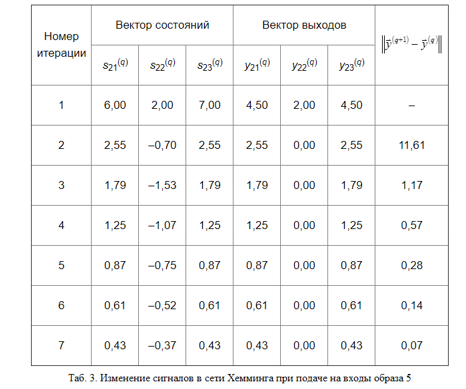
В этом случае критерий остановки был выполнен после 7-й итерации, однако уже на 2-й итерации стало понятно, что сеть Хэмминга не может отдать предпочтение 1-му и 3-му классам при отнесении входного зашумленного образа 5. В условиях малого количества входных характеристик следует сделать вывод, скорее, о том, что сеть вовсе не смогла классифицировать образ, чем о том, что она в равной степени отнесла его к двум классам.

Список литературы

1. Jesse Russell Искусственная нейронная сеть / Jesse Russell. — М.: VSD, 2012. — 265 c.
2. Потапов А.А. Новейшие методы обработки изображений// С. Никитов, Ю. Гуляев. — ФИЗМАТЛИТ. 2008, 496 стр.
3. Круглов, В.В. Искусственные нейронные сети. Теория и практика — М.: Горячая линия, 2002. — 382 c.