Заявка на публикацию
Срочная публикация научной статьи
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
О режимах заполнения барабанов котлов высокого давления при пуске из горячего состояния
Автор(ы): Крамченков Евгений Михайлович, Стерлигов Вячеслав Анатольевич, Симиниченко Станислав Викторович, Стуканев Юрий Леонидович
Рубрика: Технические науки
Журнал: «Евразийский Научный Журнал №9 2015» (сентябрь 2015)
Количество просмотров статьи: 2889
Показать PDF версию О режимах заполнения барабанов котлов высокого давления при пуске из горячего состояния
Рубрика: Технические науки
Журнал: «Евразийский Научный Журнал №9 2015» (сентябрь 2015)
Количество просмотров статьи: 2889
Показать PDF версию О режимах заполнения барабанов котлов высокого давления при пуске из горячего состояния
Крамченков Евгений Михайлович, Стерлигов Вячеслав Анатольевич
Известные соотношения, используемые для расчета температурных напряжений в барабанах паровых котлов высокого давления при заполнении водой, температура которой отличается от температуры металла [1, 2], получены с использованием допущений о мгновенном поступлении в барабан всей массы участвующей в теплообмене воды и постоянстве коэффициента теплоотдачи между стенкой и жидкостью во времени и по окружной координате. ФГБОУ ВПО "Липецкий государственный технический университет"
Симиниченко Станислав Викторович,
ООО "Техника",
Шушунов Николай Васильевич, Стуканев Юрий Леонидович
ООО "Липецкпромэкспертиза"
Указанные допущения противоречат реальной картине и не позволяют ответить на вопрос, как зависят температурные напряжения в барабане, возникающие при его заполнении, от длительности этого процесса. Сокращение времени заполнения котлов при большом числе их остановов с опережением может заметно повысить степень использования оборудования.
Ниже рассмотрена задача, в которой в опорожненный барабан в начальный момент времени начинает подаваться вода с заданным расходом и при температуре, отличной от температуры барабана.
Температурное поле в стенке барабана в рассматриваемом случае должно удовлетворять следующим соотношениям
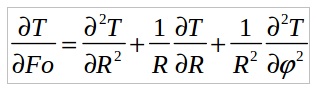 (1)
(1)где
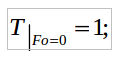 (2)
(2)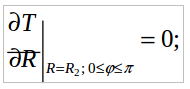 (3)
(3) (4)
(4)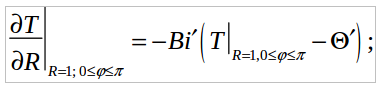 (5)
(5)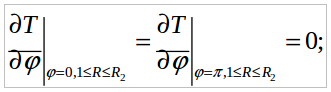 (6)
(6) Здесь
 (7)
(7)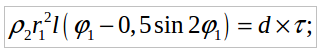 (8)
(8)где с1, с2 - удельные массовые теплоемкости металла и жидкости соответственно;
Условие (3) выражает предположение об идеальной тепловой изоляции наружной поверхности барабана. То, что тепловой поток через эту поверхность в действительности равен нулю, практически не отражается на значении температурных напряжений, обусловленных резким изменением условий теплообмена на внутренней поверхности [3].
При формулировке задачи принято также, что теплофизические свойства материала не зависят от температуры, а теплоемкость внутрибарабанных устройств пренебрежимо мала.
На практике чаще реализуется и представляет наибольший интерес случай, когда температура поступающей в барабан воды ниже температуры металла, превышающей в свою очередь температуру насыщения ts воды при атмосферном давлении, при котором происходит заполнение. Сложность определения температурного поля для названного случая обусловлена непостоянством коэффициента теплоотдачи от стенки к воде, который зависит от разности температур насыщения и поверхности (температурного напора), непрерывно уменьшающейся в процессе заполнения.
Уравнение (7) относится к периоду, когда вода еще остается недогретой до температуры насыщения. После того как эта температура достигается, значению
При
В рассматриваемой задаче наибольшие температурные напряжения действуют в аксиальном направлении. Преобразовав содержащиеся в [5] выражения для этих напряжений к безразмерному виду, получим следующую формулу:
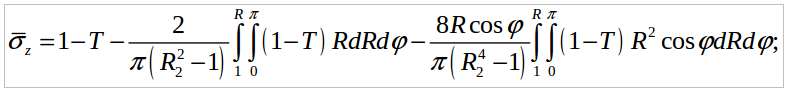 (9)
(9)где
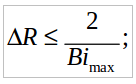 (10)
(10)где Bimax - максимальное значение критерия Био. Неравенство (10) вытекает из граничного условия (4), записанного в конечных разностях. Значение шага ΔΔ по полярному углу выбиралось из соображений точности расчета и экономии машинного времени. Шаг по времени находили из условия устойчивости расчетной схемы [7]:
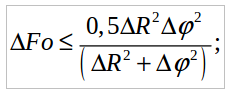 (11)
(11)При расчете с шагом ΦR, определяемым из соотношения (10), получается очень большое число узлов сетки (более 1500), что приводит к нерациональным затратам машинного времени и излишне подробной информации о температурном поле в каждый расчетный момент времени. Поэтому расчетная сетка содержала две области, в одной из которых, заключенной между R1 и Ri (
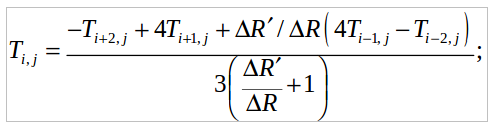 (12)
(12)где i — номер узла на радиусе; j — номер радиуса. Вычисления выполнены применительно к барабанам котлов, рассчитанных на давление 14 МПа и изготовленных из стали 16ГНМА (Dвн=1,6 м, l=16 м, s = 0,105 м) при 80 °С и различных температурах металла. При заполнении барабана с
1. Расчет прочности трубопроводов энергоустановок для условий нестационарных температурных режимов. РТМ 24.038.11-72. Введен с 01.10.73.
2. Балашов Ю. В. Расчет допустимых температурных градиентов в барабанах паровых котлов высокого давления. Электрические станции, 1972, № 9, с. 26—28.
3. Балашов Ю. В. О влиянии качества тепловой изоляции на нестационарные температурные напряжения в стенках теплосилового оборудования. — Энергомашиностроение, 1972, № 11, с. 39—40.
4. Уонг X. Основные формулы и данные по теплообмену для инженеров. Справочник.—М.: Атомиздат, 1979.—216 с.
5. Тимошенко С. П., Гудьер Дж. Теория упругости. — М.: Наука, 1975. — 576 с.
6. Ярема С. Я., Внуков А. К. К вопросу прочности барабана при пуске и остановке. — Теплоэнергетика, 1957, № 4, с. 33 36.
7. Саульев В. К. Интегрирование уравнений параболического типа методом сеток. — М.: Физматгиз, 1960.—325 с.
8. Шуп Т. Решение инженерных задач на ЭВМ. Практическое руководство: Пер. с англ. — М.: Мир, 1982. — 238 с.
9. Тепло- и массообмен. Теплотехнический эксперимент. Справочник/ Под ред. В. А. Григорьева и В. М. Зорина. М.: Энергоатомиздат, 1982.—512 с.
10. Лыков А. В. Теория теплопроводности. — М.: Высшая школа, 1967. — 599 с









