–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ь–µ—В–Њ–і –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –ї–Њ–Ї–∞–ї—М–љ–Њ–є –њ–ї–Њ—В–љ–Њ—Б—В–Є –ї–Є–љ–Є–є –љ–∞ —Ж–Є—Д—А–Њ–≤—Л—Е –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П—Е –і–∞–Ї—В–Є–ї–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е —Г–Ј–Њ—А–Њ–≤
–†—Г–±—А–Є–Ї–∞: –Ґ–µ—Е–љ–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ8 2017» (–∞–≤–≥—Г—Б—В, 2017)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 2099
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ь–µ—В–Њ–і –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –ї–Њ–Ї–∞–ї—М–љ–Њ–є –њ–ї–Њ—В–љ–Њ—Б—В–Є –ї–Є–љ–Є–є –љ–∞ —Ж–Є—Д—А–Њ–≤—Л—Е –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П—Е –і–∞–Ї—В–Є–ї–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е —Г–Ј–Њ—А–Њ–≤
–†–Њ–ґ–Є–љ–∞ –Ф–∞—А—М—П –°–µ—А–≥–µ–µ–≤–љ–∞
–Р–≥–∞—Д–Њ–љ–Њ–≤ –Р–љ–і—А–µ–є –Т–∞–ї–µ—А—М–µ–≤–Є—З
–°—В—Г–і–µ–љ—В—Л –Ѓ–£—А–У–£,
–†–Њ—Б—Б–Є—П, –≥. –І–µ–ї—П–±–Є–љ—Б–Ї
E-mail: Twayn@ya.ru
–Э–∞—Г—З–љ—Л–є —А—Г–Ї–Њ–≤–Њ–і–Є—В–µ–ї—М: –У—Г–і–Ї–Њ–≤ –Т–ї–∞–і–Є–Љ–Є—А –Ѓ–ї—М–µ–≤–Є—З
–і.—Д-–Љ.–љ., –њ—А–Њ—Д–µ—Б—Б–Њ—А,
–Ї–∞—Д–µ–і—А–∞ –≠–Т–Ь –Ѓ–£—А–У–£,
–†–Њ—Б—Б–Є—П, –≥. –І–µ–ї—П–±–Є–љ—Б–Ї
–Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –≤–Њ –Љ–љ–Њ–≥–Є—Е –Њ–±–ї–∞—Б—В—П—Е –њ—А–Є–Љ–µ–љ—П—О—В—Б—П —А–∞–Ј–ї–Є—З–љ—Л–µ –±–Є–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ –Љ–µ—В–Њ–і—Л –Є–і–µ–љ—В–Є—Д–Є–Ї–∞—Ж–Є–Є, –љ–∞–њ—А–Є–Љ–µ—А, –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –ї–Є—З–љ–Њ—Б—В–Є –њ–Њ –Њ—В–њ–µ—З–∞—В–Ї—Г –њ–∞–ї—М—Ж–∞. –Ф–∞–љ–љ—Л–є –Љ–µ—В–Њ–і –Є–і–µ–љ—В–Є—Д–Є–Ї–∞—Ж–Є–Є —И–Є—А–Њ–Ї–Њ –њ—А–Є–Љ–µ–љ—П–µ—В—Б—П –≤ –Ї—А–Є–Љ–Є–љ–∞–ї–Є—Б—В–Є–Ї–µ. –Я–Њ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є —Б –Њ—В–њ–µ—З–∞—В–Ї–Њ–≤ –Љ–Њ–ґ–љ–Њ —Б–і–µ–ї–∞—В—М –Ј–∞–Ї–ї—О—З–µ–љ–Є–µ –Њ –њ–Њ–ї–µ –Є –≤–Њ–Ј—А–∞—Б—В–µ —Б—Г–±—К–µ–Ї—В–∞. –Ю–і–љ–Є–Љ –Є–Ј –Ї—А–Є—В–µ—А–Є–µ–≤ –і–ї—П —Н—В–Њ–≥–Њ —П–≤–ї—П–µ—В—Б—П –њ–ї–Њ—В–љ–Њ—Б—В—М –ї–Є–љ–Є–є. –Т–Њ –Љ–љ–Њ–≥–Є—Е —Б—В—А–∞–љ–∞—Е, —В–∞–Ї–Є—Е –Ї–∞–Ї, –Ґ–∞–Є–ї–∞–љ–і, –Ш–љ–і–Є—П, –Р—А–≥–µ–љ—В–Є–љ–∞, –њ—А–Њ–≤–Њ–і–Є–ї–Є—Б—М –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –њ–Њ –њ–Њ–Є—Б–Ї—Г –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–µ–є –Љ–µ–ґ–і—Г –њ–ї–Њ—В–љ–Њ—Б—В—М—О –ї–Є–љ–Є–є –Љ—Г–ґ—Б–Ї–Є—Е –Є –ґ–µ–љ—Б–Ї–Є—Е –Њ—В–њ–µ—З–∞—В–Ї–Њ–≤. –Т —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л—Е —Б—В–∞—В—М—П—Е: ¬ЂDetermination of sex difference from fingerprint ridge density in northeastern Thai teenagers¬ї [1], ¬ЂSex determination from fingerprint ridge density¬ї [2], ¬ЂFingerprint ridge density in the Argentinean population and its application to sex inference: A comparative study¬ї [3], –і–µ–ї–∞–µ—В—Б—П —А—П–і –≤—Л–≤–Њ–і–Њ–≤, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –Њ —В–Њ–Љ, —З—В–Њ —Г –ґ–µ–љ—Й–Є–љ –≤ —Ж–µ–ї–Њ–Љ –љ–∞–±–ї—О–і–∞–µ—В—Б—П –±–Њ–ї–µ–µ —В–Њ–љ–Ї–Є–µ –Є —З–∞—Б—В—Л–µ –ї–Є–љ–Є–Є, —З–µ–Љ —Г –Љ—Г–ґ—З–Є–љ.
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –≤ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є, –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П –Њ –њ–ї–Њ—В–љ–Њ—Б—В–Є –ї–Є–љ–Є–є –Љ–Њ–ґ–µ—В –±—Л—В—М –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–∞ –Ї–∞–Ї —З–∞—Б—В—М –і—А—Г–≥–Є—Е –Љ–µ—В–Њ–і–Њ–≤ –Є –∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤. –Э–∞–њ—А–Є–Љ–µ—А, –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Є–љ—Д–Њ—А–Љ–∞—В–Є–≤–љ–Њ–є –Њ–±–ї–∞—Б—В–Є –Є–ї–Є –і–ї—П –њ—А–Є–Љ–µ–љ–µ–љ–Є—П —Д–Є–ї—М—В—А–∞ –У–∞–±–Њ—А–∞. [5]
–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –њ–ї–Њ—В–љ–Њ—Б—В–Є –≤ —Б—В–∞—В—М–µ –±—Г–і–µ—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–∞ —Д–Њ—А–Љ—Г–ї–∞ 4, –њ—А–µ–і–ї–Њ–ґ–µ–љ–љ–∞—П –Ф. –Ь–∞–ї—М—В–Њ–љ–Є [5], –Њ–і–љ–∞–Ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ—А—И–Є–љ, –і–ї—П –њ–Њ–і—Б—З—С—В–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–є –±—Г–і—Г—В –љ–∞—Е–Њ–і–Є—В—М—Б—П –Є–љ–∞—З–µ.
–Ф–ї—П –њ—А–Є–Љ–µ–љ–µ–љ–Є—П –њ—А–µ–і–ї–Њ–ґ–µ–љ–љ–Њ–≥–Њ –Љ–µ—В–Њ–і–∞ –љ—Г–ґ–љ–Њ –Ј–љ–∞—В—М –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О –Њ –≥—А–∞–і–Є–µ–љ—В–µ –≤ –Ї–∞–ґ–і–Њ–є –ї–Њ–Ї–∞–ї—М–љ–Њ–є –Њ–±–ї–∞—Б—В–Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П, –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П —З—В–Њ —Н—В–Є –і–∞–љ–љ—Л–µ –љ–∞–є–і–µ–љ—Л —А–∞–љ–µ–µ. –Ч–љ–∞—П, –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –≥—А–∞–і–Є–µ–љ—В–∞ –≤ —В–Њ—З–Ї–∞—Е –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П, —Г—Б–ї–Њ–≤–љ–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ—Б—В—А–Њ–Є—В—М –ї–Є–љ–Є—О –Ј–∞–і–∞–љ–љ–Њ–є –і–ї–Є–љ—Л –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Г—О –ї–Є–љ–Є—П–Љ —Г–Ј–Њ—А–∞ вАФ —А–Є—Б—Г–љ–Њ–Ї 1. –Я–Њ—Б–ї–µ —Н—В–Њ–≥–Њ —Б–ї–µ–і—Г–µ—В –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Б—З–Є—В–∞—В—М –Ј–љ–∞—З–µ–љ–Є—П –Љ–Њ–і—Г–ї—П –≥—А–∞–і–Є–µ–љ—В–∞ –≤ –Ї–∞–ґ–і–Њ–Љ –њ–Є–Ї—Б–µ–ї–µ –њ–Њ–і –ї–Є–љ–Є–µ–є –≤ –љ–µ–Ї–Є–є –±—Г—Д–µ—А B.
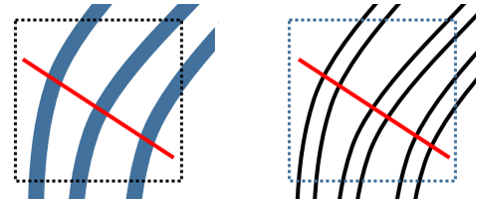
–†–Є—Б—Г–љ–Њ–Ї 1 вАФ –Ю—А–Є–≥–Є–љ–∞–ї—М–љ—Л–µ –ї–Є–љ–Є–Є —Г–Ј–Њ—А–∞ –≥—А–∞–і–Є–µ–љ—В, –ї–Є–љ–Є—П —Б—З–Є—В—Л–≤–∞–љ–Є—П
–Ґ–µ–њ–µ—А—М –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М, —З—В–Њ –≤ –±—Г—Д–µ—А–µ B –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –≥—А–∞–і–Є–µ–љ—В–∞, –≤ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ–Љ —Г–Ј–Њ—А—Г –Є –≤ —Ж–µ–љ—В—А–µ —Б –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–є —В–Њ—З–Ї–Њ–є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П:![]() ,
, ![]()
–Э–∞ –і–∞–љ–љ–Њ–Љ —Н—В–∞–њ–µ —Б–ї–µ–і—Г–µ—В –њ–Њ—Б—З–Є—В–∞—В—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –≤ –Ї–∞–ґ–і–Њ–є –Є–Ј —Б–Њ—Е—А–∞–љ–µ–љ–љ—Л—Е —В–Њ—З–µ–Ї —Д—Г–љ–Ї—Ж–Є–Є ![]() –Ф–ї—П —Н—В–Њ–≥–Њ –Љ–Њ–ґ–љ–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤ —В–Њ—З–Ї–µ:
–Ф–ї—П —Н—В–Њ–≥–Њ –Љ–Њ–ґ–љ–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤ —В–Њ—З–Ї–µ: ![]()
–Ґ–Њ–≥–і–∞, –≤ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–Љ —Б–ї—Г—З–∞–µ: ![]()
–Т—Л–њ–Њ–ї–љ–Є–≤ —А–∞—Б—З–µ—В—Л –Є –Ј–∞–њ–Є—Б–∞–≤ —А–µ–Ј—Г–ї—М—В–∞—В—Л –≤ –±—Г—Д–µ—А –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ–≥–Њ —А–∞–Ј–Љ–µ—А–∞ ![]() , –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –Ј–∞–њ–Є—Б–∞–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –љ–∞–њ–Њ–Љ–Є–љ–∞—О—В –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є
, –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –Ј–∞–њ–Є—Б–∞–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –љ–∞–њ–Њ–Љ–Є–љ–∞—О—В –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є ![]() –Є–ї–Є
–Є–ї–Є ![]() . –У–і–µ —В–Њ—З–Ї–Є —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞ (–Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞) –њ—А–Є—Е–Њ–і—П—В—Б—П –љ–∞ –≥—А–∞–љ–Є—Ж—Л –ї–Є–љ–Є–є вАФ —А–Є—Б—Г–љ–Њ–Ї 2.
. –У–і–µ —В–Њ—З–Ї–Є —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞ (–Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞) –њ—А–Є—Е–Њ–і—П—В—Б—П –љ–∞ –≥—А–∞–љ–Є—Ж—Л –ї–Є–љ–Є–є вАФ —А–Є—Б—Г–љ–Њ–Ї 2.

–†–Є—Б—Г–љ–Њ–Ї 2 вАФ –Я—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ –≥—А–∞–і–Є–µ–љ—В—Г
–Я–Њ –Ј–љ–∞—З–µ–љ–Є—П–Љ –≤ –±—Г—Д–µ—А–µ ![]() –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є —В–Њ—З–Ї–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ –Є, –Є–Љ–µ—П –Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —А–∞—Б—Б—В–Њ—П–љ–Є–є, –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є 4.
–Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є —В–Њ—З–Ї–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ –Є, –Є–Љ–µ—П –Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —А–∞—Б—Б—В–Њ—П–љ–Є–є, –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є 4.
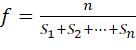 , –≥–і–µ (4)
, –≥–і–µ (4)
n вАФ —З–Є—Б–ї–Њ —А–∞—Б—Б—В–Њ—П–љ–Є–є –Љ–µ–ґ–і—Г —В–Њ—З–Ї–∞–Љ–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞, –∞ ![]() вАФ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —А–∞—Б—Б—В–Њ—П–љ–Є—П –Љ–µ–ґ–і—Г —Б–Њ—Б–µ–і–љ–Є–Љ–Є —В–Њ—З–Ї–∞–Љ–Є.
вАФ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —А–∞—Б—Б—В–Њ—П–љ–Є—П –Љ–µ–ґ–і—Г —Б–Њ—Б–µ–і–љ–Є–Љ–Є —В–Њ—З–Ї–∞–Љ–Є.
–Я—А–Є —Н—В–Њ–Љ –Љ–Њ–ґ–љ–Њ —Г—З–Є—В—Л–≤–∞—В—М –љ–µ –≤—Б–µ —В–Њ—З–Ї–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞, –∞ –ї–Є—И—М —В–µ, —З—В–Њ –≤—Л—И–µ –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –њ–Њ—А–Њ–≥–∞. –І—В–Њ –њ–Њ–Ј–≤–Њ–ї–Є—В —Г—З–µ—Б—В—М –ї–Є—И—М –љ–∞–Є–±–Њ–ї–µ–µ –Ј–љ–∞—З–Є—В–µ–ї—М–љ—Л–µ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –≥—А–∞–і–Є–µ–љ—В–∞, –Ї–Њ—В–Њ—А—Л–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В –≥—А–∞–љ–Є—Ж–∞–Љ –ї–Є–љ–Є–є.
–†–µ–Ј—Г–ї—М—В–∞—В —А–∞–±–Њ—В—Л –∞–ї–≥–Њ—А–Є—В–Љ–∞ –Љ–Њ–ґ–љ–Њ –≤–Є–і–µ—В—М –љ–∞ —А–Є—Б—Г–љ–Ї–µ 3. –°–≤–µ—В–ї—Л–µ —Г—З–∞—Б—В–Ї–Є –Њ–±–Њ–Ј–љ–∞—З–∞—О—В –≤—Л—Б–Њ–Ї—Г—О –њ–ї–Њ—В–љ–Њ—Б—В—М –ї–Є–љ–Є–є, —В–µ–Љ–љ—Л–µ вАФ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –љ–∞–Њ–±–Њ—А–Њ—В.
–°—А–µ–і–Є –і–Њ—Б—В–Њ–Є–љ—Б—В–≤ –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ–Њ–≥–Њ –Љ–µ—В–Њ–і–∞ –Њ—В–Љ–µ—В–Є–Љ –µ–≥–Њ —Б–Ї–Њ—А–Њ—Б—В—М —А–∞–±–Њ—В—Л, –Њ–љ–∞ –і–Њ—Б—В–Є–≥–∞–µ—В—Б—П –Ј–∞ —Б—З—С—В –∞–љ–∞–ї–Є–Ј–∞ –ї–Є–љ–Є–Є, –∞ –љ–µ –Њ–±–ї–∞—Б—В–Є, –Ї–∞–Ї –≤ –љ–µ–Ї–Њ—В–Њ—А—Л—Е –Є–Ј —Б—Г—Й–µ—Б—В–≤—Г—О—Й–Є—Е –Љ–µ—В–Њ–і–Њ–≤, –Ї—А–Њ–Љ–µ —В–Њ–≥–Њ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –≥—А–∞–і–Є–µ–љ—В–∞, —З—В–Њ –і–∞–µ—В —З–µ—В–Ї–Є–µ –Њ—В–Ї–ї–Є–Ї–Є –љ–∞ –≥—А–∞–љ–Є—Ж–∞—Е –ї–Є–љ–Є–Є –Є –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Є–Ј–±–µ–ґ–∞—В—М –њ–Њ–Љ–µ—Е –љ–∞ —Д–Њ–љ–µ.

–†–Є—Б—Г–љ–Њ–Ї 3 вАФ –Ю—А–Є–≥–Є–љ–∞–ї—М–љ–Њ–µ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ –Є –µ–≥–Њ –њ–ї–Њ—В–љ–Њ—Б—В—М –ї–Є–љ–Є–є
–°–њ–Є—Б–Њ–Ї –ї–Є—В–µ—А–∞—В—Г—А—Л
- ScienceDirect. Determination of sex difference from fingerprint ridge density in northeastern Thai teenagers [–≠–ї–µ–Ї—В—А–Њ–љ–љ—Л–є —А–µ—Б—Г—А—Б]. URL: http://www.sciencedirect.com/science/article/pii/S2090536X15000738 (–і–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П 26.06.2017).
- BioMedSearch. Sex determination from fingerprint ridge density [–≠–ї–µ–Ї—В—А–Њ–љ–љ—Л–є —А–µ—Б—Г—А—Б]. URL: http://www.biomedsearch.com/article/Sex-determination-from-fingerprint-ridge/187844335.html (–і–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П 26.06.2017).
- ResearchGate. Fingerprint ridge density in the Argentinean population and its application to sex inference: A comparative study [–≠–ї–µ–Ї—В—А–Њ–љ–љ—Л–є —А–µ—Б—Г—А—Б]. URL: https://www.researchgate.net/publication/282946342_Fingerprint_ridge_density_in_the_Argentinean_popu... (–і–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П 26.06.2017).
- Davide Maltoni, Dario Maio, Anil K. Jain, Salil Prabhakar. Handbook of Fingerprint Recognition. Second Edition. Springer-Verlag London Limited 2009 вАФ 506—Б.









