Математическая модель оценивания вероятности возникновения ошибок в устройствах памяти

Хорошо известно, что для исследования поведения сложных объектов в условиях воздействия внешней среды широко используются методы математического или натурного моделирования. При изучении особенностей хранения информации в динамических микросхемах памяти, на основе которых реализуется оперативная память компьютера (ДБИС ОЗУ), применяется ПО Matlab/Simulink. Пакет Simulink является составной частью системы моделирования MATLAB и поставляется вместе с ней. Основа его работы — принципы визуально ориентированного программирования с использованием моделей, представленных в виде блоков, структурированных по разделам библиотеки.

С помощью специализированных блоков Simulink построим модель байтовой ячейки динамической памяти, работающей в условиях естественного радиационного фона, и проведем сравнительный анализ помехоустойчивости хранения данных при отсутствии и использовании избыточного кода Хемминга [6].

Влияние альфа-частиц на надежность хранения информации в ОЗУ.

Динамические микросхемы памяти обладают следующими особенностями:

— запоминающим элементом (ЗЭ) ДБИС ОЗУ является конденсатор С_з, образованный поликремниевой областью канального транзистора (рисунок 1). Под этой областью создается потенциальная яма, которая пуста при хранении «1» и заполнена электронами при хранении «0»;

— ограниченное время хранения заряда запоминающим элементом. Через интервал времени, равный периоду регенерации 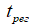, информацию, хранимую в ЗЭ, необходимо восстанавливать (регенерировать). Наличие дефекта вызывает ток утечки, который может разрядить запоминающую емкость за время, меньшее 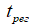, что приведет к потере информации .

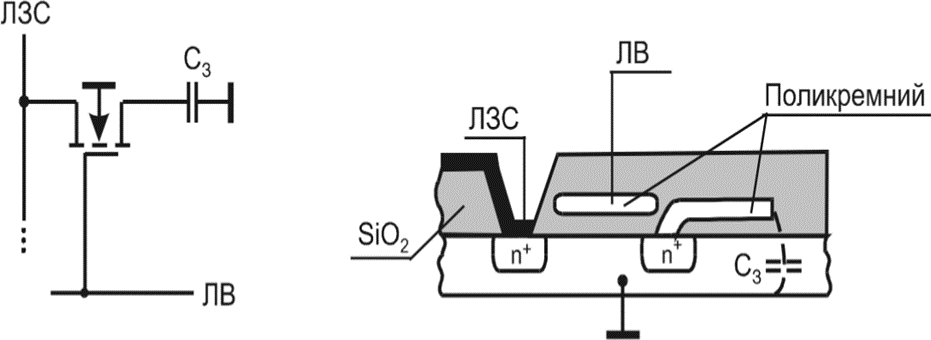
Рисунок 1 — Схема ячейки динамического ОЗУ:

Содержащиеся в керамических корпусах микросхем остатки урана и тория излучают альфа — частицы. Попадания альфа — частиц в ЗЭ и разрядную шину выбираемого ЗЭ вызывают переход логического состояния «1» в «0». Попадания альфа-частиц в невыбранные разрядные шины и ЗЭ приводят к переходу логического «0» в «1». Попадания альфа — частиц в усилители считывания и схемы управления являются источниками сбоев обоих типов: перехода логического состояния «1» в «0» и логического «0» в «1».

Для исправления ошибок хранения информации в ДБИС ОЗУ широко используются специальные корректирующие коды Хемминга, обнаруживающие и исправляющие однобитовые ошибки в n-разрядных словах. Так, для 8-разрядного слова информации требуется четыре дополнительных контрольных бита (таблица 1).

Таблица 1 — Распределение разрядов 12-битного слова

Номер бита	12	11	10	9	8	7	6	5	4	3	2	1
Бит данных	D8	D7	D6	D5		D4	D3	D2		D1
Контр. биты					P8				P4		P2	P1

Контрольные биты определяются по правилам, представленным формулой

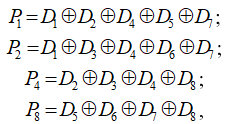
где ⊕ — поразрядная логическая операция «исключающее или».

Процедура моделирования. На основе данных в среде моделирования MATLAB/Simulink разработана имитационная модель битовой ячейки ДБИС ОЗУ, а также собрана байтовая ячейка памяти 8×1, защищенная избыточным кодом Хемминга.

В разработанной модели битовой ячейки ДБИС ОЗУ (рисунок 2) используются типовые блоки пакета Simulink: логические блоки: И, ИЛИ, НЕ; памяти, порты ввода и вывода, триггерный блок. Модель имеет входы WL (линия выборки) и BL (линия записи), выход (OUT) работает как продолжение ЛЗС, через него осуществляется чтение бита. Наличие триггера, обозначенного Cs1, определяет модель как квазидинамическую ячейку, поскольку хранение данных зависит от изменения состояния триггера, а разряд конденсатора во время хранения не учитывается.

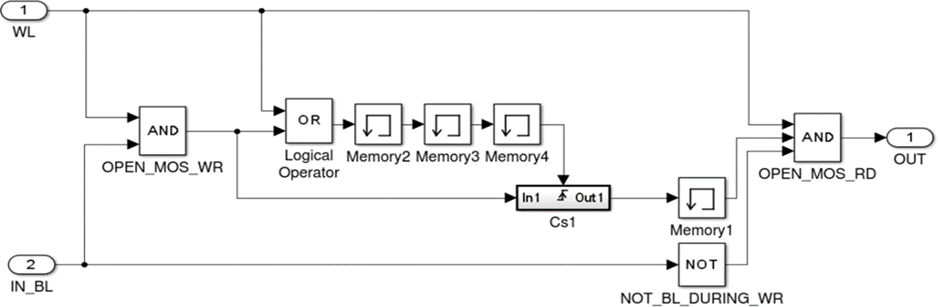
Рисунок 2 — Модель битовой динамической ячейки памяти

Также были построены следующие модели:

— битовая ячейка с возможностью принудительной записи нуля или единицы при подаче импульса на входы ERR0 и ERR1. Так моделируется пролет альфа-частицы через каждую битовую ячейку;

— усилитель считывания, который представляет собой триггер, реагирующий на импульс, поступающий при чтении содержимого битовой ячейки. По стробу OE осуществляется защелкивание значения считанного бита;

— блок REFRESH, реализующий восстановление записанного в ячейке памяти бита после операции чтения. В общей схеме эксперимента этот блок помещается между генератором управляющих сигналов (RAS, WE, выбор строки WL) и ячейкой памяти. Схемы перечисленных выше устройств объединены с помощью блока Subsystem в отдельные макроблоки: BitCell, SA и REFRESH, на основе которых собрана структура 8-разрядной ячейки динамического ОЗУ (рисунок 3);

— генератор ошибок, имитирующий воздействие альфа-частиц (рисунок 4). Схема выполнена на основе библиотечного блока генератора случайной бинарной последовательности с распределением Бернулли. Для распределения Бернулли задается вероятность P — непоявления альфа — частицы (событие «0»), соответственно, вероятность появления альфа — частицы равна (1-p), где 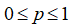. Также используются 4 блоков Unbuffer, с помощью которых реализуется возможность появления ошибки в любом бите 4-разрядного слова, эмулированного в эксперименте. Поскольку для моделируемой 8-разрядной ячейки требуется четыре дополнительных контрольных бита (таблица 2) в модели генератора ошибок используются четыре заглушки (Terminator);

генератор управляющих сигналов, в котором управляющие сигналы реализуются блоком Signal Builder (рисунок 5).

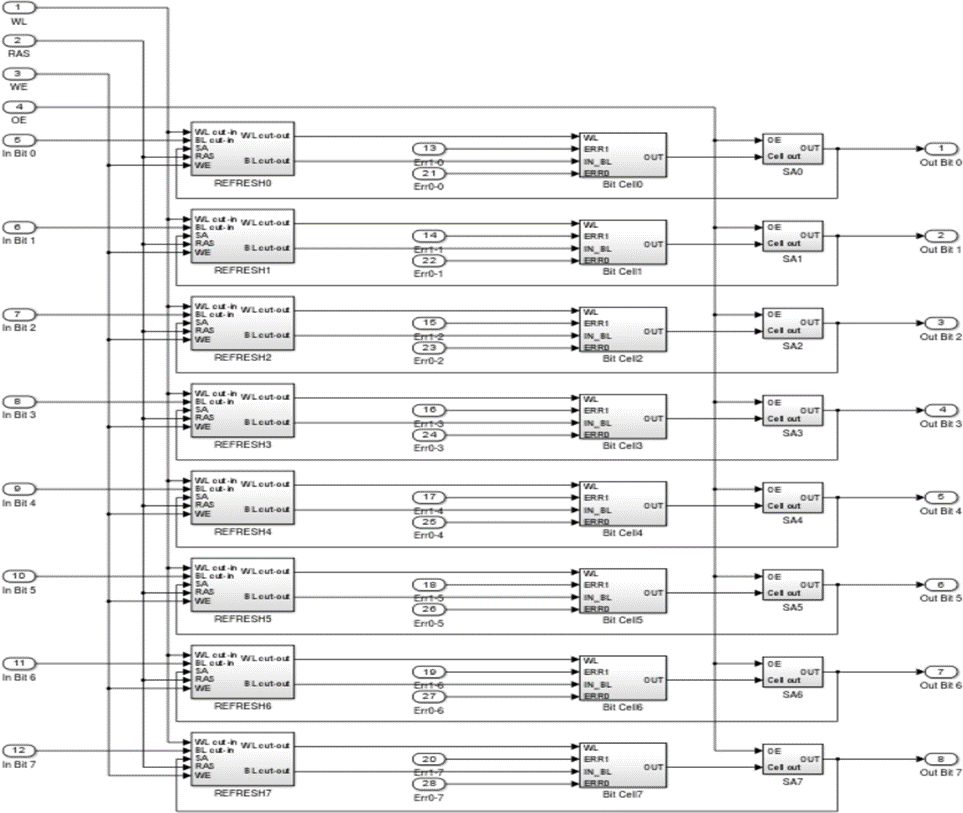
Рисунок 3 — Модель байтовой ячейки динамической памяти

В модели используется только одна байтовая ячейка, поэтому можно обойтись без строба выбора столбца. По переднему фронту сигнала регистрации ошибки (EDS) выявляется несоответствие считанного и записанного битов данных. При проведении эксперимента количество несоответствий суммируется и определяется общее количество выявленных ошибок.


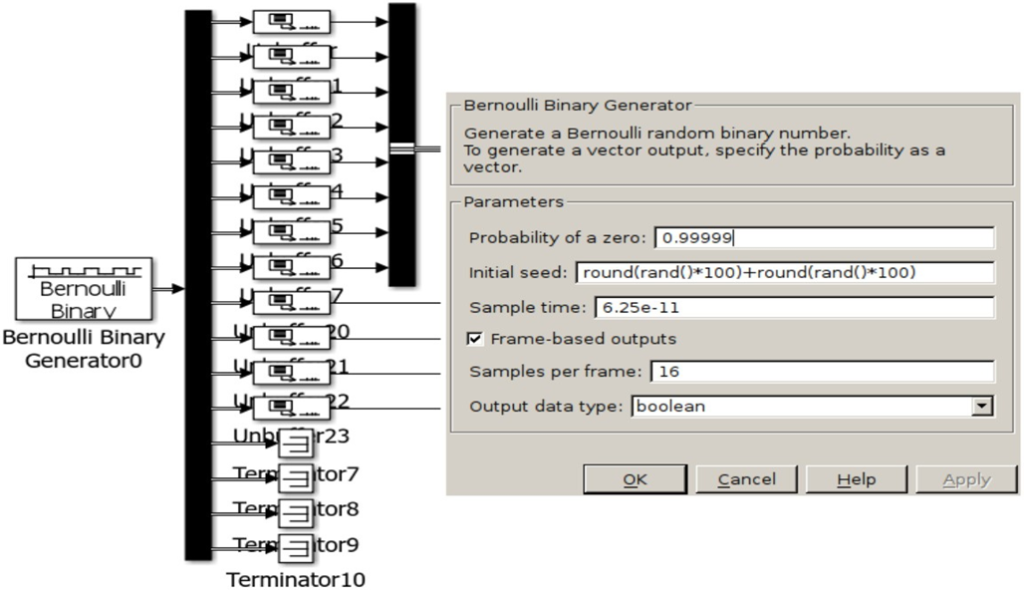
Рисунок 4 — Модель генератора ошибок и настройки блока генератора Бернулли

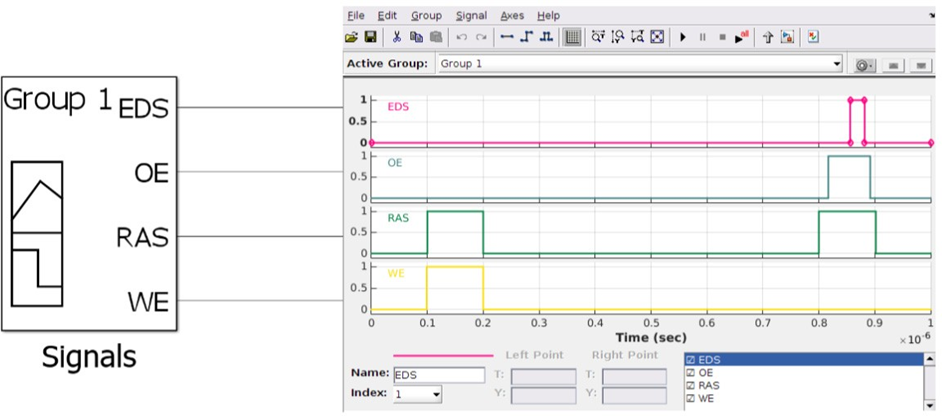
Рисунок 5 — Модель генератора управляющих сигналов, временные диаграммы его работы

Схема проведения эксперимента. Из описанных выше блоков построена схема, с помощью которой исследуется влияние кодов Хэмминга на количество ошибок памяти, вызванное воздействием альфа-частиц. Помимо указанных выше блоков, в схеме эксперимента используются библиотечные функциональные блоки кодера и декодера Хемминга.

Эксперимент запускался с помощью разработанного m-файла (Matlab) (рисунок 6).

Рисунок 6 — Текст m-файла для запуска эксперимента

Использовались следующие параметры моделирования: время моделирования — 1 мкс, шаг моделирования — 1 нс.

После проведения 1000 опытов получены результаты моделирования в виде вектора ошибок в рабочей области Simulink — Workspace (рисунок 7).

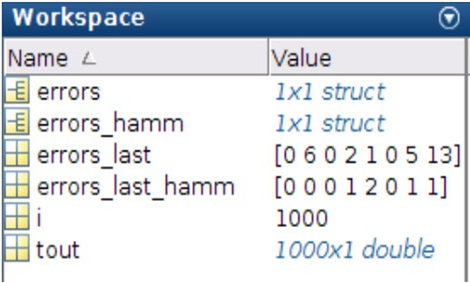
Рисунок 7 — Результаты моделирования

Каждый элемент вектора — сумма накопленных несоответствий между записанным и считанным битом по всему эксперименту. В векторе errors фиксируются ошибки хранения 8-разрядного слова без применения кода Хэмминга, в переменной errors_hamm — накопленные ошибки хранения с применением помехозащищенного кодирования. Поскольку коды Хэмминга позволяют исправлять одиночные ошибки, в векторе errors_last_hamm представлены ошибки большей разрядности. Полученный результат позволяет судить об эффективности применения кода Хэмминга в системах хранения информации: количество ошибок в векторе errors_last в 5,4 раза превышает количество ошибок, накопленное в векторе errors_last_hamm.