Использование электромагнитного микроволнового излучающего два линейно поляризованных пучка в сторону цели интерферометра для создания на неё механического воздействия

Данная работа описывает Испытательный стенд и  метод использования двух сфокусированных на заданную цель свободного пространства, идущих в одном направлении узконаправленных когерентных линейно поляризованных моно гармонических СВЧ электромагнитных потоков, для оказания механического давления на предмет, находящийся на их пути [1].

 Для этой цели автор предполагает использование электромагнитного излучения  одной из моделей "Двух лучевого микроволнового электромагнитного когерентного интерферометра (ДЛЭКИ)",   изложенных в Описании  Патента РФ № 2482446 [2].

Как следует из текста работы [1, 2] два упомянутые линейно поляризованные когерентные взаимно ортогональные потоки радиоволн несущей частоты f созданы двумя СВЧ возбудителями; один из которых является Щелевым возбудителем электромагнитных  волн, относящийся к типу  Магнитного Диполя Герца (МДГ), а другой - например, Рупорный СВЧ возбудитель, относящийся к Электрического Диполя Герца (ЭДГ) типу [1].

На Рис.1.  схематично представлен предполагаемый вид испытательного стенда (ИС) для иллюстрации сущности настоящей работы.

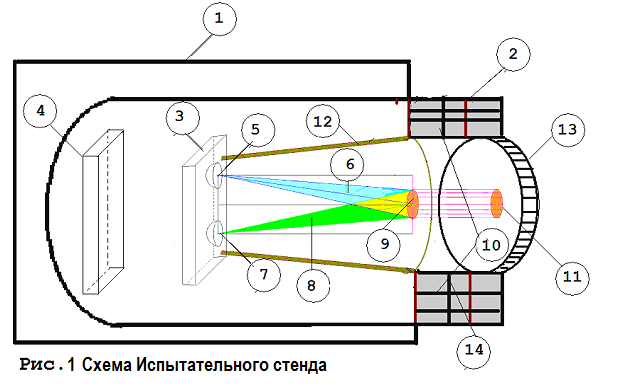
1. Описание функционирования Испытательного Стенда (Рис.1).

Двух лучевой микроволновый электромагнитный когерентный интерферометр (ДЛЭКИ), условно обозначенный цифрой 1 на Рис. 1 в соответствии с  работой  [2] состоит из двух антенн, одна из которых содержит щелевого типа возбудитель электромагнитного потока, а другая содержит рупорного типа возбудитель электромагнитного потока.

Центральные оси упомянутых узконаправленных СВЧ взаимно ортогональных линейно поляризованных потоков (условно обозначенные на Рис. 1 цифрами  6 и 8) лежат в одной плоскости и пересекаются на заранее определённом расстоянии R внутреннего ограниченного первого пространства (камеры I), ограниченного конической формы оболочкой (условно обозначенной на Рис.1 цифрой 12),  выполненной из диэлектрического и не намагничивающегося материала.  Цилиндрическая  из  материала высокой плотности оболочка (условно обозначенная на Рис.1 цифрой 14) ограничивает второе пространство (камеры I I ) направленного потока квантов волн де Бройля [3],  возникшего в зоне пересечения упомянутых СВЧ электромагнитных пучков в результате их когерентной резонансной интерференции [1].

Узко направленные потоки СВЧ электромагнитного излучения от упомянутых МДГ и ЭДГ возбудителей (п. 6,8 Рис.1) интерферометра (ДЛЭКИ) (п. 3 Рис.1) фокусируются на виртуальной поверхности (п. 9 Рис.1), расположенной вблизи выхода из тоннеля, образованного первой конической формы оболочкой (п. 12 Рис.1)  камеры I, и направлен на специально размещённый (п.13 Рис.1) "Барьер" в торце камеры I I, являющейся деталью (п. 2  Рис.1) повышенной прочности, жёстко закреплённой к корпусу объекта (п. 1. Рис.1), внутренняя поверхность которой в сечении п.11 Рис.2 "Барьера" 13, принимает весь напор направленного потока квантов Волн Де Бройля, при этом, как будет показано ниже, сила оказываемого воздействия которого определяется числом поглощенных его квантов в материале "Барьера".

Цифрой 4 условно обозначен блок источников электрического питания, систем автоматической защиты, управления, контроля и устройств связи, подключаемый к указанному интерферометру (ДЛЭКИ) (п. 3 Рис.1).

Описание моделей устройств и результаты экспериментальных исследований этого типа интерферометра (ДЛЭКИ) проведённые собственноручно автором,  необходимые для практического создания данного Испытательного стенда описаны подробно в [2].

Физическая модель, используемая в настоящей работе, подробно изложена автором в Описании Изобретения Патента РФ №2530223 [1]

2. Способность направленного потока квантов материальных волн де Бройля создавать давление [кг/кв.м] на преграду будь это материал барьера или материал среды 13, встречаемого на пути его прямолинейного продвижения со скоростью V_К  (близкой или равной скорости света) во внешнем пространстве может быть разъяснена следующим образом. Очевидно, что возможность получения давления на преграду подтвердит возможность создания механического воздействия образовавшегося потока квантов материальных волн де Бройля на "Барьер" с силой F[н., или кг-силы] .

Собственно, отысканию максимально возможного теоретического значения для величины этой силы F посвящена настоящая работа автора.

В материальной среде со значением (удельной или объемной) плотности ρ [кг/куб.м] поток квантов Ф_Ω материальных волн де Бройля ослабевает из за  взаимодействия квантов Ω (передавая полностью свою энергию ζ_Ω и свою величину "количества движения" М_Ω материальным частицам среды) по мере продвижения в ней на L метров по экспоненциальному закону:

Ф_Ω (L) = Ф_Ω (0)e^-αρL  (2 -1), где

Ф_Ω (0), Ф_Ω (L) соответственно поток Волн Де Бройля в начале и после прохождения в среде пути длиной L[м],

α - градиент уменьшения, зависящий от единиц измерения, структуры вещества, и от ряда физических его свойств, требующий экспериментальной коррекции, [кг/кв.м].

Всё это означает, что давление σ_Ω (L) потока квантов Волн де Бройля является функцией вида:

σ_Ω (L) = σ_Ω (1 - e^-αρL)  (2 - 2).

Таким образом, создаваемое давление потока на предмет, находящейся на  пути потока корпускул материальных волн де Бройля в конкретный момент времени будет тем сильнее, чем выше плотность ρ среды препятствия и чем больше его толщина (L). Для вакуума поток волн де Бройля без уменьшения своей интенсивности устремляется на любое расстояние, пока не встретит на своём пути препятствие. Для сравнения значения ρ ряда твердых, жидких и газообразных веществ (большинство данных  с порталов:  www.edu.glasprav.ru\info и www.calc.ru) приведены в таблице 1.

Таблица 1.

Твердое вещество	Плотность кг/куб.м.	Твердое вещество	Плотность кг/куб.м
Алюминий	2700	Барий	3500
Ванадий	6000	Висмут	9800
Вольфрам	19100	Железо	7800
Золото	19300	Иридий	22400
Медь	8900	Никель	8900
Свинец	10500	Серебро	10500
Титан	4500	Молибден	10220
Латунь	8500	Осмий	22600
Олово	7300	Цинк	7100
Сталь	7800	Чугун	7000
Платина	21500	Корунд	4000
Уран обеднённый	19050	Стекло	2500
Мрамор	2700	Кирпич	1800
Оргстекло	1200	Капрон	1100
Полиэтилен	920	Парафин	900
Лёд	700	Дуб	700
Сосна	400	Пробка	240
Жидкость	Плотность кг/куб.м	Жидкость	Плотность кг/куб.м
Ртуть	13600	Вода морская	1030
Вода чистая	1000	Керосин, спирт	800
Масло машинное	900	Нефть	800
Газ	Плотность кг/куб.м	Газ	Плотность кг/куб.м
Воздух(20 гр. С)	1,290	Водяной пар	0,590 (100гр. С)
Азот	1,250	Кислород	1,430
Гелий	0,180	Водород	0,090

Число N_ф фотонов  потока радиоволн частоты несущей f от каждой антенны, пересекающих площадку А_эфф поверхности в заданный момент времени t и в заданном месте возникновения когерентной резонансной интерференции, например, в точке пересечения их центральных осей может быть определено с помощью выражения:

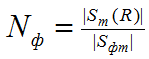(2 - 3), где

|S_m(R)| -  абсолютное значение вектора Умова - Пойнтинга на расстоянии R от Антенны.

|S_фm| - абсолютное значение вектора Умова - Пойнтинга одиночного фотона. В соответствии с изложенном в [1]:

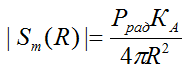      (2 - 4)

           (2 - 5), поэтому

       (2 - 6)

          (2 - 7) ,

где  f – частота несущей потока электромагнитных волн, [Гц],

λ  - длина их волны, [м],

с₀  - скорость света в вакууме, [м/сек]

c₀ = 2,997825 10 ⁸   

h - Постоянная Планка, [Дж сек]  h = 6,3 10 ^-34.

Р_рад - мощность  энергии, излучаемая в пространство каждой из СВЧ антенн, [Вт];

К_А - коэффициент усиления (по мощности) каждой из СВЧ антенн.

Отвлекаясь от реальной картины диаграмм направленности СВЧ антенн, считаем, что образующая боковая поверхность потока, излучаемая каждой из СВЧ антенн, представляет из себя поверхность правильного кругового конуса. Величину К_А ориентировочно можно определить по формуле 

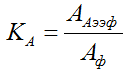 (2 - 8),

где А_{А эфф}, А_ф – площадь излучения СВЧ Антенны (например, её основного зеркала) и площадь поперечного сечения фотона, соответственно [кв.м].

 (2 - 9)

        (2 - 10)

          (2 - 11)

D_A, r_ф - диаметр СВЧ Антенны (например, её основного Зеркала) и радиус СВЧ фотона, соответственно, [м].

Таким образом, с учётом (2 - 4)

(2 - 12)

СВЧ фотоны двигаются в открытом пространстве со скорость света с₀, обладают количеством движения или импульсом силы М_ф [кг м/сек или н сек] и энергией ζ_ф [дж][3]:

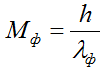    (2 - 13)           

       (2 - 14)

В результате когерентной резонансной интерференции радиоволновых потоков 6 и 8 (рис. 1, рис. 2) и резонансного захвата разнородных фотонов [1]. «Антифотона» от одной антенны с СВЧ возбудителем МГД типа и фотона от другой антенны с СВЧ возбудителем ЭГД типа они аннигилируют на расстоянии R от СВЧ Антенн (5 и 7), передавая своей энергию 2ζ_ф и своё количество движения 2 М_ф возникшей корпускуле Ω. Корпускула Ω продолжает прямолинейное движение со скоростью V_K по биссектрисе направлений движения исходной пары "фотон – антифотон". Область этого процесса можно видеть на рис. 1 и рис. 2 на пересечении электромагнитных потоков 6 и 8. 

Поэтому для "Количества движения" образовавшейся корпускулы Ω и её энергии ζ_Ω можно записать

    (2 - 15)    

        (2 - 16)

Образованная, напоминающая нейтрино, или антинейтрино, возникающие в результате аннигиляции гамма - квантов в Атомной Физике [3], корпускула Ω (только для диапазона СВЧ с энергией на несколько порядков меньшей, чем у нейтрино), двигающаяся со скоростью V_К, и, обладая количеством движения М_Ω, в соответствие с представлением де Бройля [3] так же является квантом материальных волн де Бройля с  длиной волны λ_Ω :

    (2 - 17)

При учете (2 - 15) следует, что длина λ_Ω материальных волн де Бройля в два раза меньше длины волны λ_ф радиоволновых потоков 6, 8, излучаемых СВЧ антеннами 5 и 7:

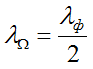        (2 - 18).

Разумеется, что длина одиночного фотона λ_ф радиоволновых потоков равна длине волны λ данных СВЧ излучений. Итак, полученная корпускула Ω и одновременно материальный квант волн Де Бройля (см. [3], стр. 171) в  соответствии со Специальной теорией относительности А.Эйнштейна может обладать и массой покоя m₀  (находящейся в покое по отношению к наблюдателю, движущемуся в месте с ней) и динамической массой m_д, являющейся фактической массой m_Ω этого одиночного кванта Ω волн де Бройля (для наблюдателя находящегося в неподвижной системе отсчёта).

  (2 - 19)           

Полная энергия ξ_Ω этого материального кванта волн де Бройля состоит из кинетической энергии ζ_ΩК: и энергии потенциальной (энергии покоя) ζ_Ω0 .

          (2 - 20)

   (21)

Будем различать два возможных сценария образования материального кванта Ω волн де Бройля в результате резонансного захвата разнородной пары фотонов потока радиоволн 6 и 8:

Сценарий А: когда кинетическая энергия 2ζ_ф этой пары фотонов потоков СВЧ радиоволн вся переходит кинетической энергии образованного кванта Ω материальных волн де Бройля.

В этом случае 

(2 - 22),

с учётом (2 - 19) и (2 - 21) m_Ω0 = 0; ς_Ω0 = 0; 

(2 - 23).

  Таким образом, (2 - 24) и

(2 - 25)

Сценарий Б: когда кинетическая энергия 2ζ_ф этой пары фотонов потоков СВЧ радиоволн 6 и 8 Рис. 1  не вся переходит в кинетическую энергию образованного кванта Ω волн де Бройля.

В этом случае

(2 - 26);

(2 - 27);

(2 - 28)

и из (19): 

(2 - 29)

Исследования показали, что для этого случая практически имеется одно лишь решение:

(2 - 30);

(2 - 31)

с учётом (2 - 28);

(2 - 32);

(2 - 33); 

(2 - 34)

Видим, что в данном случае 71% общей энергии

(2 - 35)

образованного кванта Ω  уходит на его внутреннее устройство, и лишь 29% общей его энергии ζ_Ω уходит на его кинетическую энергию ζ_ΩК.

при этом 

(2 - 36);

с учётом (2 - 15) 

(2 - 37)

Итак, для сценария А:

(2 - 38);

(2 - 39);

(2 - 40).

для сценария Б:

(2 - 41);

(2 - 42);

 

 (2 - 43);

(44).

Основное выражение количественной оценки давления σ [н/кв.м] направленного потока квантов материальных волн де Бройля можно получить путём нахождения:

(2 - 45), где

 - давление на поверхность предполагаемого препятствия одиночного кванта Ω направленного потока волн де Бройля [н /кв.м].

 - скорость прохождения квантов Ω направленного потока материальных волн де Бройля сквозь заданную поверхность [1(квант)/сек].

(2 - 46),

(2 - 47), где

d_Ω - диаметр кванта Ω [м],

τ_Ω - длительность взаимодействия одиночного кванта потока волн де Бройля с частицей материала препятствия при полной передаче ей своего количества движения и своей энергии [сек],

 с учётом (2 - 6) и (2 - 46 и 2 - 47)

(2 - 48);

(2 - 49);

(2 - 50)

и с учётом (2 - 47, 2 - 49), в соответствии с (2 - 40 и 2 - 44) и с учётом (2 - 39 и 2 - 42)                         

(2 - 51), где

ξ₁ = 1 для сценария А (2 - 52а) и

ξ₁ = 2^0.5 для сценария Б (2 - 52б),

с учётом (2 - 47, 2 - 50, 2 - 51):

(53)

и с учётом (45, 47, 52 и 53) и (38, 41) можем записать, что

(2 - 54), где

ξ= 1 для Сценария А и

ξ = 0,71 для Сценария Б (2 - 55).

В итоге, можем записать окончательно максимально теоретически возможное значение для силы действующей направленным потоком квантов материальных волн де Бройля на препятствие на их пути:

(2 - 56), где

∆t – интервал времени воздействия на препятствие [сек],

F – действующая на препятствие сила [н],

∆A – поперечное сечение препятствия, если оно меньше эффективного поперечного сечения А_эфф направленного потока волн де Бройля в данном месте и в данное мгновение [кв.м] на расстоянии R.

В принципе, если известна масса объекта препятствия находящегося в свободном пространстве  на расстоянии R от антенн ДЛЭКИ то, зная силу F, воздействующую в течении отрезка времени ∆t на препятствие, и площади А_эфф сечения пучка волн де Бройля поверхности взаимодействия объекта препятствия (цели на которую направлен этот поток) можно определить значение ускорения а приданное этому объекту препятствия в течении отрезка времени  ∆t и значение скорости v его движения в конце этого интервала времени ∆t.

Конечно формула (2 - 56) предполагает, что 100% число квантов Ω данного потока передало свою энергию и количество движения  веществу "Барьера" Испытательного стенда.

3. Как было отмечено автором в Описание Патента РФ № 2482446 [2]:

Сила механического воздействия переднего фронта возникшего направленного потока квантов Волн де Бройля на препятствие его движению прямо пропорциональна

а)  интервалу времени его воздействия на преграду,

б) величине эффективной площади взаимодействия данного потока с поверхностью преграды для заданного расстояния  R до неё,

в) Коэффициенту (усиления) направленности СВЧ антенны,

г) Мощности электромагнитной энергии, излученной одной из антенн и обратно пропорциональна величине расстояния R от антенн до препятствия, длине волны λ, излучаемых антеннами  ДЛЭКИ  СВЧ электромагнитных потоков.

4. Формула (2 - 56) может принять следующий вид:

(4 - 1)

принимая о внимание, что 

(4 - 2)        

где η - эффективность взаимодействия квантов Ω потока Волн де Бройля с веществом препятствия ("Барьера" Испытательного стенда)

5. Для примера произведём оценку силы воздействия  F на "Барьер" Испытательного стенда, представленного на Рис.1 при значениях величин:

а) R = 5 м,

б) К=4000,

в) Р_рад = 10 Ватт,

г) λ = 0.01 м, 

д) ξ =0.7 , а η = 0.1,

е) ∆ = 1 сек.

ж) диаметр основного зеркала антенн D = 0.2 м

С учётом формулы (4 - 1) получим, что F = 2763.5 Ньютон, таким образом  ожидается механическое воздействие на "Барьер"  порядка 276 Кг -сила.

6. В заключении хотелось отметить, как изложено в [1] и [2], автор собственноручно сконструировал, изготовил и провел испытание ещё в период 1992 - 1996 г.г. двух моделей ДЛЭКИ на частотах порядка 6 ГГц  с использованием самых современных по тем временам СВЧ деталей и измерительных систем.

В результате этих испытаний обнаружил новый эффект:

механического воздействия продукта не электромагнитной природы на размещённую преграду на расстоянии нескольких порядков выше длины волны от антенн модели ДЛЭКИ, образованного в результате интерференции идущих раздельно в одном направлении узконаправленных взаимно ортогональных моногармоничных когерентных потоков при условии обеспечения высочайшей стабильности по частоте и  отсутствия взаимного фазового сдвига в точке фокусирования  этих взаимно ортогональных СВЧ потоков в заданной точке пространства.

ЛИТЕРАТУРА

1. А.Б. Ляско "Способ преобразования в открытом пространстве двух направленных в одну сторону линейно поляризованных моногармоничных потоков электромагнитных волн в направленный поток волн де Бройля", Патент РФ № 2530223 от 12 Августа 2014 г. по Заявка на Изобретение №2013110738  от 12.03.2013, ФИПС РФ, Москва.

2. А.Б. Ляско "Электромагнитный микроволновый, излучающий два  линейно поляризованных пучка в сторону цели интерферометр", Патент РФ на Изобретение № 2482446 по Заявке на Изобретение №2011150442 от 13 Декабря , 2011 г., Бюллетень №14, 20.05.2013, ФИПС РФ, Москва.

3. Смит Г. «Введение в атомную физику», Москва, Иностранная литература, 1948, стр. 169-173, §66 «Гипотеза де Бройля», §67 «Параллелизм волновых и корпускулярных представлений».

4. А.Б. Ляско "Электромагнитный двигатель", Заявка на Изобретение № 2013139104, Бюллетень № 6 от 27.08.2015, ФИПС РФ, Москва.