In Traffic Flow Model with Transition from Disorder to Order

Abstract

Traffic flow is a collection of multiple phases, each of which is realized under different conditions. In this paper, we propose a new technique to investigate the dynamical transitions between them. A type of the control signal has been added to the traffic system at a given site (signal point) of the single lane highway. Under the effect of the control signal, the velocity of the vehicle which passes the signal point will be changed periodically. Our method is tested for the deterministic NaSch traffic model. The simulation results demonstrate that the disorder states in deterministic NaSch traffic model can be suppressed, and the different types of periodic states would occur.

Introduction

Recently, numerous empirical date and numerical simulations have been made in understanding the traffic dynamics. Some complex physical phenomena have been observed in traffic pattern, including the existence of multiple phases, the hysteresis in transitions between the traffic phases and the long survival time of traffic jams.^{1_'²_'^3} In generally, the traffic flow state is relative simple for low density values, and is complex for intermediate high-density values^{1_'²_'^4}. In the latter case, chaotic phenomena in traffic system have been observed^{5}. From practical point of view such complex behavior in traffic system always bring some safety and jam problems, such as the states of vehicles at the intersections in city network. Thus it would be interesting to further study the transition of the traffic flow state from complex to simple.

A complex traffic pattern consists of numerous traffic jams, where the average velocity of vehicles is lower than the minimum possible average velocity in free flow. It has been suggested that at a bottleneck, the transitions between different types of the traffic pattern can be found. In {6} the dynamical transition from the free flow to the choking flow was studied by carrying out a numerical simulation for the mean-field equation. B.S. Kemer presented the results of an empirical study of spatial –temporal traffic patterns at highway bottlenecks^{7}.

Some alternative parameterization of the defect (or, disordered) sites in the NaSch model were outlined. Some effects of the static hindrances on vehicular traffic have also been investigated following alternative approaches¹¹¹⁰¹. In this paper, we designate a type of the control signal at a given site of the road and thus control the disorder states in traffic system. In this case, we note that not only the traffic accident can be decreased, but also the capacity of the network can also be improved in city traffic. To our knowledge, this work explicitly shows cellular automata for the first time.

NaSch traffic model

NaSch traffic model is a one - dimensional probalilistic cellular automation model^{11} Which is an extension of the ASEP (Asymmetric exclusion proceses). In NaSch traffic model, the road is divided into L cells numbered by i=1,2 L, and the time is discrete.

Each site can be either empty or occupied by a vehicle with integer velocity v=0>1....>V_maz, where is the maximum velocity. The underlying dynamics of NaSch model is governed by the updated rules applied at discrete time steps. All sites are simultaneously updated according to four successive steps.

1. Acceleration : Increase by 1 if .

2. Slowing down: decrease to = d if necessary (d is the number of empty cells in front of the vehicle.)

3. Randomization: decrease by 1 with randomization probability p if p>0.

4. Movement : move vehicle sites forward.

The random braking probability or the rule (s) for random braking can give rise to a rich variety of physical phenomena in the generalizations and extensions of the NaSch model^(12,13). The effects of the different types of quenched randomness which are associated with the vehicles and the road have been investigated. In this case, the motion is characterized by abrupt changes in vehicles velocities, especially, nondeterministic acceleration as well as overreaction while slowing down. This is crucially important for the complex behavior formation of traffic flow.

In our method, we designate a type of the control signal at a given site (signal point) of the road. When the vehicle passes the signal point; the velocity of the vehicle will be changed at the next time step, i.e. and . Where is a square wave,

a is a parameter which can be adjusted. Explicitly, when the vehicle passes the signal point, the update rules are as follows

1) Acceleration : increase by 1 if

2) Slowing down : decrease to = d if necessary.

3) Disturbing :

1. and

2. decrease to = d if necessary.

4) Movement : move vehicle sites forward.

In step (3) a type of the periodic control signal is added to the traffic system. As the time proceeds, under the effect of the control signal, the velocity of the vehicle which passes the signal point will be disturbed. Since flux is equal to the inverse of the average time-headway, much more detailed information is contained in the distribution of the time headway such as the temporal organization of the vehicles. In the view of time series, the character of the overall dynamics of the systems is reflected in the behavior of any dynamics variable. Here we are mainly focused on dynamical behavior by analyzing the traffic series of the time headways, but for comparison the traffic series of the distance headway is also considered.

There are N vehicles moving on a road of L sites. The signal point is designed at the middle of the road. A given site of the road is taken as the observation point. When the control signal is added to the system. We start to record the time that the vehicles occupy the observation point. We use t_i to represent the time that i­th vehicle occupies the observation point. The traffic series {x_i}, i = 1,…, K, is recorded as the time-headways at the observation point, x_i=t_i+l-t_i,. The investigations are mainly focused on = 5, and the boundary condition for NaSch traffic model is periodic. In this paper a system of L = 400 is considered. The length of the observation time is T=1000, and the first 500 are discarded to avoid transistent.

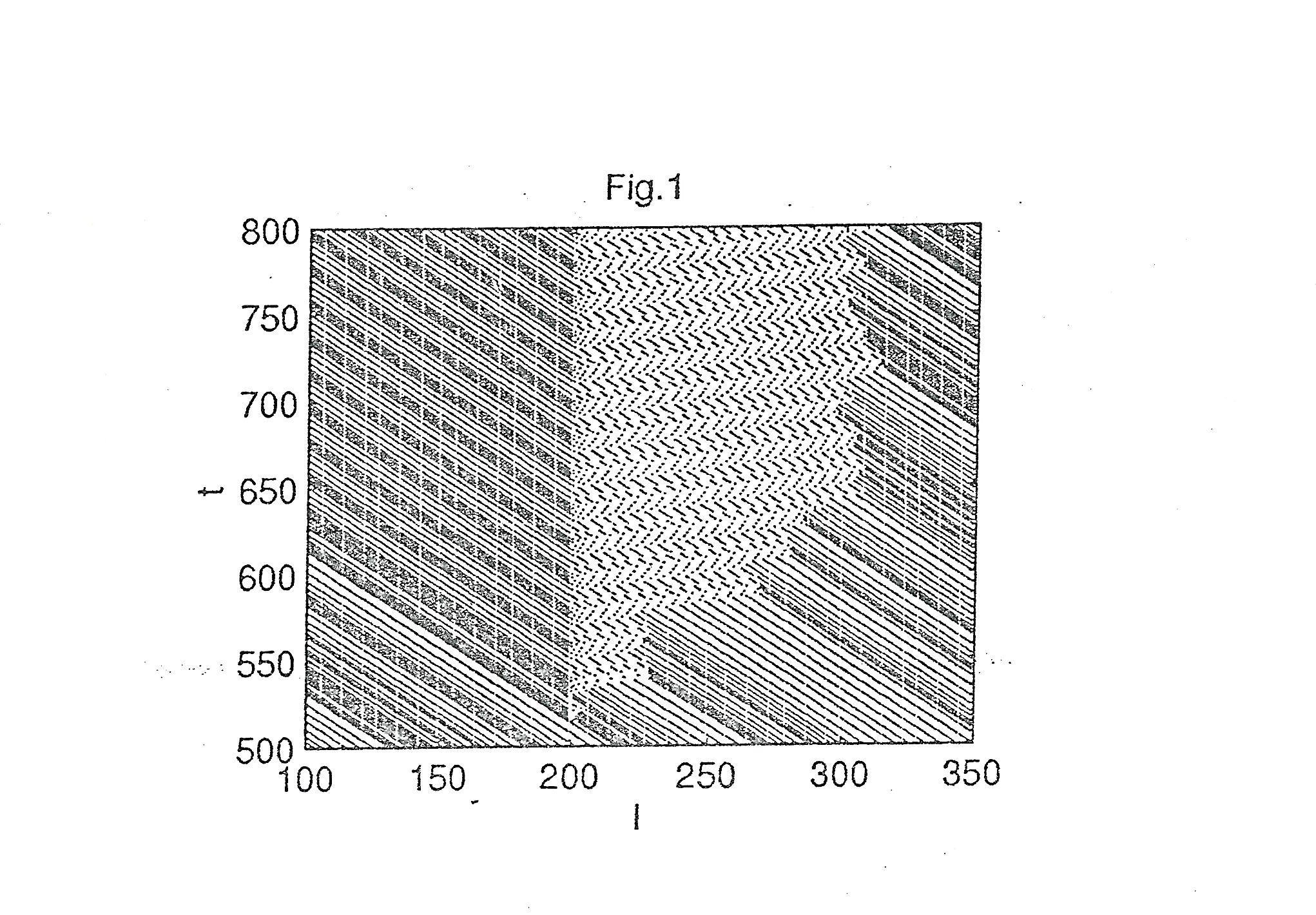
While the vehicle passes the signal point, it is disturbed by the control signal. The local space –time diagram of the traffic flow is shown in fig. 1. In fig. 1 the control signal is added to the traffic system at the time t = 500. from fig. 1 we can observe that the space-time diagram consists of the macroscopic jam and the macroscopic free-flow region, and the homogeneous states of the traffic flow have a lifetime after which their decay leads to a phase separated state. The results indicate that under the effect of the control signal the traffic flow exhibits the macroscopic space-time diagrams into different types of the pattern over time.

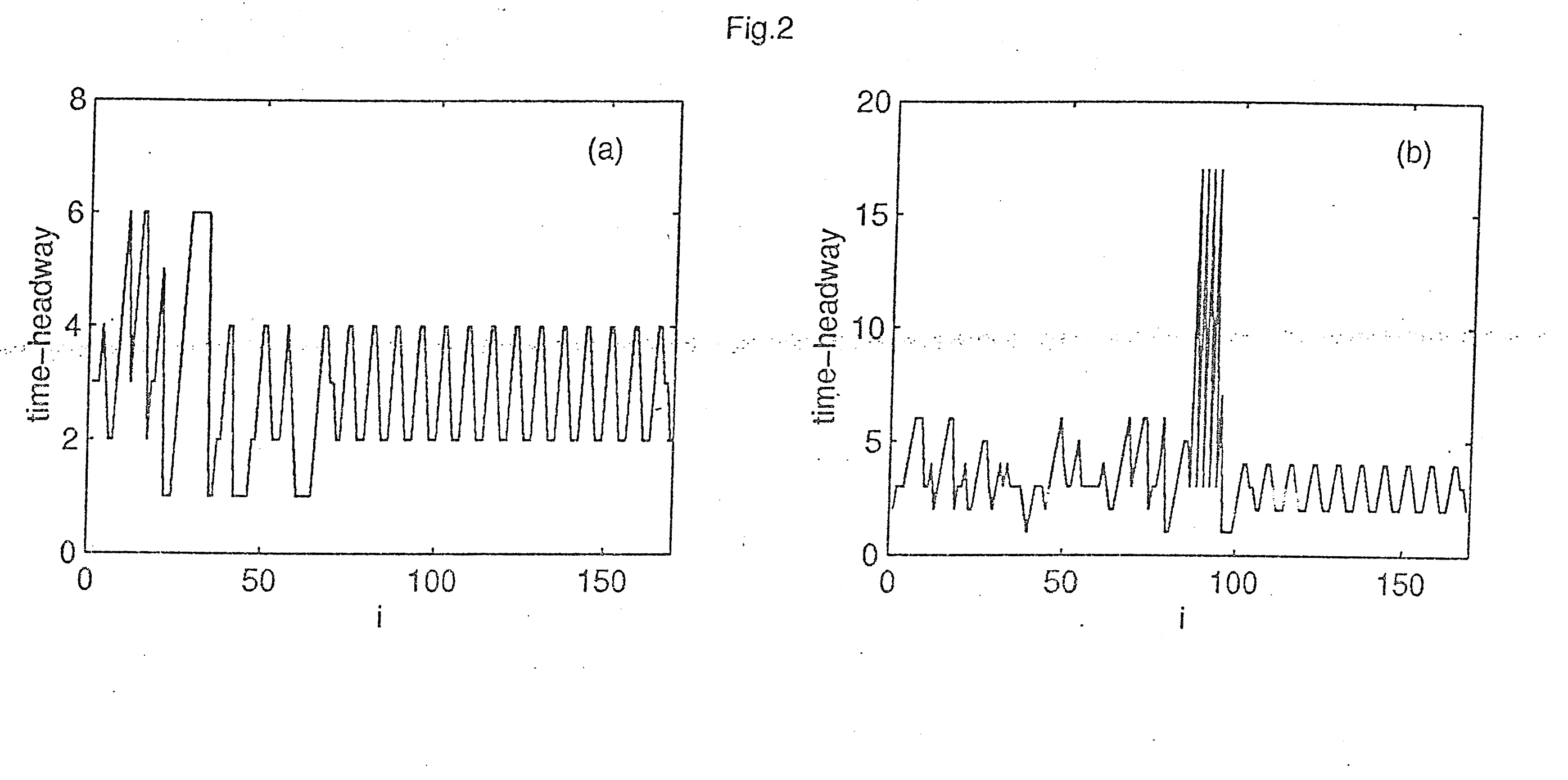
The traffic series of the time headway for the density p = 0.3 is shown in Fig 2. In Fig 2 (a) and (b), we can clearly see that the dynamical states of the traffic flow are disorder at first, and then the traffic flow transit from the disorder states to periodic states with different amplitudes, A part from these we can observe that not only the amplitude of the periodic motion varies with the observation time, but also it varies with the observation site. The simulation results demonstrate that the localized control methods proposed in our method has global effects whereby the states of the traffic flow can be transited form disorder to order.

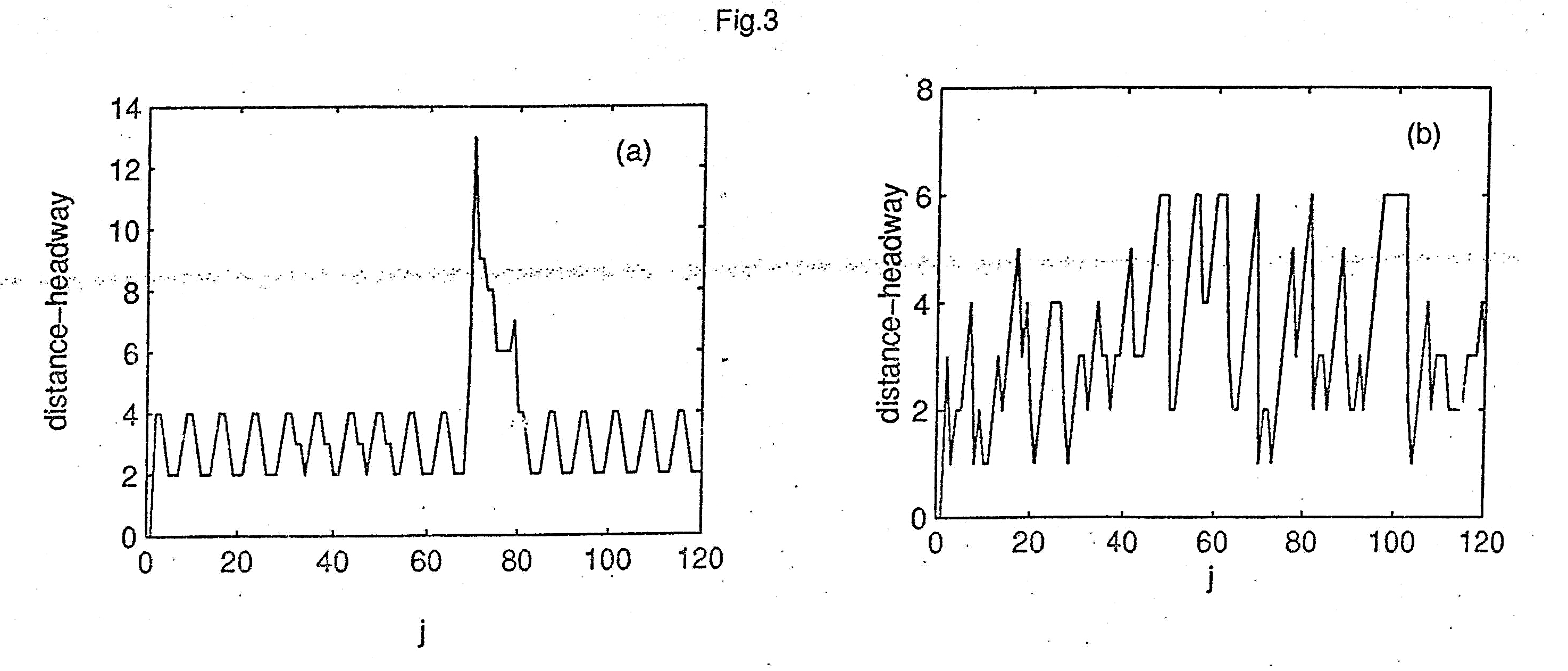
In order to get information on the spatial organization of the vehicles one can measure the variation of the distance headway on the road. The traffic series is recorded as the distance headway at a given time t, where is the distance from the j-th vehicle to (j+1) –th vehicle. Fig 3 shows the traffic series of the distance headway time t = 1000. Here the abscissa represents the vehicle on the road, and the parameter a is set to 10 in Fig 3(a). From Fig 3(a) it can be clearly observed that the traffic series of the distance – headway is periodic i.e. the traffic flow is at order state under the effect of the control signal. However in Fig 3(b), we find that the variation of the traffic series of the distance headway is disorder. The results mean that the traffic flow can be transited from the disorder state to the periodic state by the control signal.

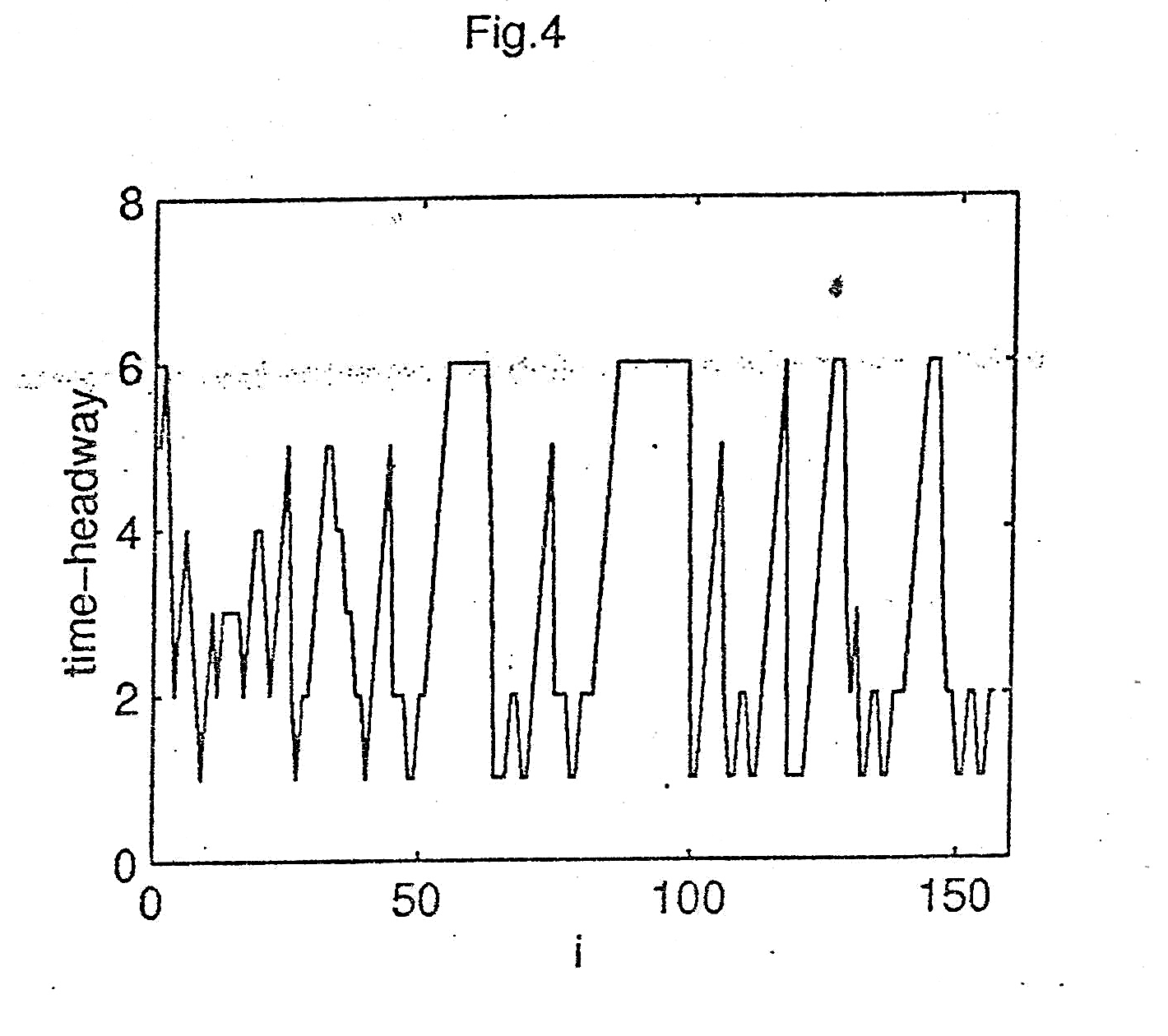
In our method a is an adjustable parameter. If we change the value of the parameter a, the periodicity of the square wave will be changed. Fig 4 shows the traffic series of the time headway for p = 0.3 and a = 15. Comparing Fig 4 with Fig 2(a), it is clearly found that the variation of the time headway in Fig 4 is random as the time proceeds, however, the variation of the time headway is periodic after the sufficient transient time in Fig. 2 (a)

The simulation results demonstrate that only by we choose a suitable parameter a, the traffic flow state can be transited from disorder to order.

Conclusion

In conclusions, the effect of the control signal can be considered as external disturbing. It suppresses the disorder state in traffic flow, and forms the periodic state with different amplitude. On the other hand, our simulations indicate that the traffic flow state in the deterministic NaSch model is sensitive to the fluctuation of the velocity, and therefore is metastable. While the external disturbing is added to the system, the system moves from the metastable state to the stable state.

In this paper, one of the conditions that the disturbing can be introduced is . This means that the disturbing does not exist as . In fact, if the condition that the disturbing can be introduced in , all vehicles in traffic system will be at motionless etc. This is insignificant. In the other word, if the condition that the disturbing can be introduced includes d = , the velocity of the vehicles may be is larger than the maximum velocity . This is not permissible in the NaSch traffic model.

References

1. Kemer B S and Rehborn H 1996 Phys. Rev. E 53 R 4275

2. Kemer B S and Rehborn H 1997 Phys. Rev. Lett 79 4030

3. Elad Tomer, Leonid Safonov and Shlomo Havlin 2000 Phys. Rev Lett. 84 382

4. Kemer B S 1999 Phys. World 12 25

5. Nagatani T 1999 Phys. Rev. E 60 1535

6. Nagatani T 2001 Physcia A 300 558

7. Kemer B S 2002 Phys. Rev. E 65 046138

8. Csahok Z and Vicsek T 1994 J. Phys. A 27 L 591

9. Emmerich H and Rank e 1995 Physica A 216 435

10. Nagatani T 1997 J. Phys. Soc. Japan 66 1928

11. Nagel K and Schreckenberg M 1992 J. Phys. I 2 2221

12. Nagel K and Paczuski M 1995 Phys Rev E 51 2909

13. Benjamin S C, Johnson N F and Hui P M 1996 J. Phys. A 29 3119

Figure

Figure 1 The local space time diagram of the traffic flow for p = 0.3, a = 10 Figure 2 The traffic series of the time headway for p = 0.3, a = 10, Part (a) is obtained at 1 = 100, and part (b) is obtained at 1 = 300 (b)

Figure 3 The traffic series of the distance headway obtained at the time t = 1000 for p=0.3,

Part (a) is with control signal, and part (b) is without control signal

Figure
4 The traffic series of the time headway obtained at the observation
site 1
= 100 for p = 0.3, a = 15