–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Т—Л–≤–Њ–і —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –і–ї—П –Љ–Є–Ї—А–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е –Є –Љ–∞–Ї—А–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ
–†—Г–±—А–Є–Ї–∞: –§–Є–Ј–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ12 2015» (–і–µ–Ї–∞–±—А—М 2015)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 8313
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Т—Л–≤–Њ–і —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –і–ї—П –Љ–Є–Ї—А–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е –Є –Љ–∞–Ї—А–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ
–С–∞—В–∞–љ–Њ–≤ –Ь–Є—Е–∞–Є–ї –°–µ–Љ–µ–љ–Њ–≤–Є—З,
–Ї–∞–љ–і–Є–і–∞—В —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –љ–∞—Г–Ї, –і–Њ—Ж–µ–љ—В –Ї–∞—Д–µ–і—А—Л 207, –Ь–Р–Ш, –†–Њ—Б—Б–Є—П
alsignat@yandex.ru
–Р–љ–љ–Њ—В–∞—Ж–Є—П: –Ю—Б–љ–Њ–≤–∞–љ–љ—Л–µ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є (—В–∞–Ї–Є–µ, –Ї–∞–Ї ¬Ђ–≤–Њ–ї–љ—Л –Љ–∞—В–µ—А–Є–Є¬ї –і–µ –С—А–Њ–є–ї—П, ¬Ђ–њ—А–Є–љ—Ж–Є–њ –љ–µ–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ—Б—В–Є¬ї –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞, –Њ—В—Б—Г—В—Б—В–≤–Є–µ —А–∞–Ј–Љ–µ—А–Њ–≤ –Є —В—А–∞–µ–Ї—В–Њ—А–Є–Є –і–≤–Є–ґ–µ–љ–Є—П —Г —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж, –∞ —В–∞–Ї–ґ–µ –Є—Б—В–Њ—А–Є—П –≤–Њ–Ј–љ–Є–Ї–љ–Њ–≤–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞), –і–Њ —Б–Є—Е –њ–Њ—А –љ–µ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –ї–Њ–≥–Є—З–µ—Б–Ї–Є –Њ–±–Њ—Б–љ–Њ–≤–∞–љ—Л. –Ш–љ—В–µ—А–µ—Б –Ї –Є—Б—В–Њ–Ї–∞–Љ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ –µ—Й–µ —В–µ–Љ, —З—В–Њ –њ–µ—А–µ–і–Њ–≤—Л–µ —А—Г–±–µ–ґ–Є –љ–∞—Г–Ї–Є –≤ –Њ–±–ї–∞—Б—В–Є –Є–Ј—Г—З–µ–љ–Є—П —Б—В—А—Г–Ї—В—Г—А–љ–Њ–є –Њ—А–≥–∞–љ–Є–Ј–∞—Ж–Є–Є –Љ–∞—В–µ—А–Є–Є - —Б—В—А—Г–љ–љ—Л–µ —В–µ–Њ—А–Є–Є, –±–∞–Ј–Є—А—Г—О—Й–Є–µ—Б—П –љ–∞ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ, –љ–∞—Е–Њ–і—П—В—Б—П –≤ –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –љ–µ–њ—А–µ–Њ–і–Њ–ї–Є–Љ—Л—Е (–љ–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і) –Ј–∞—В—А—Г–і–љ–µ–љ–Є—П—Е. –≠—В–Њ –Ј–∞—Б—В–∞–≤–ї—П–µ—В –≤–µ—А–љ—Г—В—М—Б—П –Ї –њ–µ—А–µ–Њ—Б–Љ—Л—Б–ї–µ–љ–Є—О –Њ—Б–љ–Њ–≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Д–Є–Ј–Є–Ї–Є.
–Т –љ–Є–ґ–µ–Є–Ј–ї–Њ–ґ–µ–љ–љ–Њ–є —Б—В–∞—В—М–µ –њ—А–µ–і–ї–Њ–ґ–µ–љ–∞ –Љ–Њ–і–µ–ї—М —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –±–ї—Г–ґ–і–∞—О—Й–µ–є –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —З–∞—Б—В–Є—Ж—Л (–Њ–±–ї–∞–і–∞—О—Й–µ–є —А–∞–Ј–Љ–µ—А–Њ–Љ –Є —В—А–∞–µ–Ї—В–Њ—А–Є–µ–є –і–≤–Є–ґ–µ–љ–Є—П), –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–є —Г–і–∞–ї–Њ—Б—М:
- –≤—Л–≤–µ—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞;
- –њ—А–Є–і–∞—В—М –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –Я–ї–∞–љ–Ї–∞ ƒІ –Ї–Њ–љ–Ї—А–µ—В–љ–Њ–µ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ;
- –Њ–±–Њ—Б–љ–Њ–≤–∞—В—М –њ–µ—А–µ—Е–Њ–і –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є (–≤ —В.—З. –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є) —Б–Є—Б—В–µ–Љ—Л –Ї –µ–µ –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—О –±–µ–Ј –њ—А–Є–≤–ї–µ—З–µ–љ–Є—П –Є–і–µ–Є –Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–Є ¬Ђ–≤–Њ–ї–љ –Љ–∞—В–µ—А–Є–Є¬ї –і–µ –С—А–Њ–є–ї—П –Є ¬Ђ–њ—А–Є–љ—Ж–Є–њ–∞ –љ–µ–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ—Б—В–Є¬ї –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞.
–Я—А–Є —Н—В–Њ–Љ –≤—Л—П–≤–ї–µ–љ—Л —Г—Б–ї–Њ–≤–Є—П –Є –≥—А–∞–љ–Є—Ж—Л –њ—А–Є–Љ–µ–љ–µ–љ–Є—П –Њ–±–Њ–±—Й—С–љ–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –Ї –Њ–њ–Є—Б–∞–љ–Є—О —П–≤–ї–µ–љ–Є–є, –Ї–∞–Ї –Љ–Є–Ї—А–Њ–Љ–Є—А–∞, —В–∞–Ї –Є –Љ–∞–Ї—А–Њ–Љ–Є—А–∞.
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –њ—А–Њ–Љ–µ–ґ—Г—В–Њ—З–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В ¬Ђ–Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є n-–≥–Њ –њ–Њ—А—П–і–Ї–∞ n —А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ, —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞¬ї –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Є–Љ–µ–љ–Є–Љ –≤–Њ –Љ–љ–Њ–≥–Є—Е –Њ–±–ї–∞—Б—В—П—Е —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Є —А–∞–і–Є–Њ—Д–Є–Ј–Є–Ї–Є.
–Ъ–ї—О—З–µ–≤—Л–µ —Б–ї–Њ–≤–∞: —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞, —Н–ї–µ–Ї—В—А–Њ–љ, –њ–ї–Њ—В–љ–Њ—Б—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є, —З–∞—Б—В–Є—Ж–∞, —Е–∞–Њ—В–Є—З–µ—Б–Ї–∞—П —В—А–∞–µ–Ї—В–Њ—А–Є—П, –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ.
1. –£—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ –Є –њ—А–Њ–±–ї–µ–Љ—Л –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є –њ–∞—А–∞–і–Є–≥–Љ—Л
–Ю–і–љ–Њ–є –Є–Ј –Њ—Б–љ–Њ–≤–љ—Л—Е –Ј–∞–≥–∞–і–Њ–Ї –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤—Б–µ—Е —Б–Њ–≤—А–µ–Љ–µ–љ–љ—Л—Е –њ—А–Њ–і–Њ–ї–ґ–µ–љ–Є–є –і–∞–љ–љ–Њ–є —В–µ–Њ—А–Є–Є, –Њ—Б—В–∞–µ—В—Б—П —В–∞–є–љ–∞ –њ–Њ—П–≤–ї–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞. –Ю—В—Б—Г—В—Б—В–≤–Є–µ –ї–Њ–≥–Є—З–µ—Б–Ї–Є –Њ–±–Њ—Б–љ–Њ–≤–∞–љ–љ–Њ–≥–Њ –≤—Л–≤–Њ–і–∞ –і–∞–љ–љ–Њ–≥–Њ –Є—Б—Е–Њ–і–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ –≤–ї–Є—П–µ—В –љ–∞ —А–∞–Ј–≤–Є—В–Є–µ –љ–∞—И–Є—Е –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є –Њ —Б—В—А—Г–Ї—В—Г—А–љ–Њ–є –Њ—А–≥–∞–љ–Є–Ј–∞—Ж–Є–Є –Љ–∞—В–µ—А–Є–Є.
–£—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ –Є–Љ–µ–µ—В –≤–Є–і
(1)
–≥–і–µ ќ® = ќ® (x,y,z,t) вАУ –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–∞—П —Б–Њ—Б—В–Њ—П–љ–Є–µ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є
—З–∞—Б—В–Є—Ж—Л;
U (x, y, z) вАУ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л;
ќ® вАУ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞;
m вАУ –Љ–∞—Б—Б–∞ —З–∞—Б—В–Є—Ж—Л.
–°—З–Є—В–∞–µ—В—Б—П, —З—В–Њ —Н—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –±—Л–ї–Њ –њ–Њ–ї—Г—З–µ–љ–Њ –≠—А–≤–Є–љ–Њ–Љ –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ (1887 вАУ 1961) –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Є–љ–і—Г–Ї—В–Є–≤–љ—Л—Е –Є –і–µ–і—Г–Ї—В–Є–≤–љ—Л—Е –њ—А–µ–і–њ–Њ—Б—Л–ї–Њ–Ї, —Б–ї–Њ–ґ–Є–≤—И–Є—Е—Б—П –Ї 1926 –≥–Њ–і—Г –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є —Б–≤–Њ–є—Б—В–≤ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж.
–Ю—Б–Њ–±–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≤ —В–Њ –≤—А–µ–Љ—П –Є–Љ–µ–ї–∞ –Є–і–µ—П –Ы—Г–Є –Т–Є–Ї—В–Њ—А–∞ –і–µ –С—А–Њ–є–ї—П (1892 вАУ 1987) –Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –≤–Њ–ї–љ–Њ–≤—Л—Е —Б–≤–Њ–є—Б—В–≤ –Љ–∞—В–µ—А–Є–Є. –Ы—Г–Є –і–µ –С—А–Њ–є–ї—М, —Б–Њ–њ–Њ—Б—В–∞–≤–Є–≤ –њ—А—П–Љ–Њ–ї–Є–љ–µ–є–љ—Г—О —В—А–∞–µ–Ї—В–Њ—А–Є—О –і–≤–Є–ґ–µ–љ–Є—П —Б–≤–Њ–±–Њ–і–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –Є —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є–µ –ї—Г—З–∞ —Б–≤–µ—В–∞, –њ—А–Є—И–µ–ї –Ї –≤—Л–≤–Њ–і—Г, —З—В–Њ –њ—Г—В—М –њ—А—П–Љ–Њ–ї–Є–љ–µ–є–љ–Њ –і–≤–Є–ґ—Г—Й–µ–є—Б—П –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –Є –ї—Г—З —Б–≤–µ—В–∞ –Њ–њ–Є—Б—Л–≤–∞—О—В—Б—П –Њ–і–љ–Є–Љ –Є —В–µ–Љ –ґ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –ѓ–Ї–Њ–±–Є, –≤—Л—В–µ–Ї–∞—О—Й–Є–Љ –Є–Ј —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–Њ–≥–Њ –њ—А–Є–љ—Ж–Є–њ–∞ ¬Ђ—Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞ –і–µ–є—Б—В–≤–Є—П¬ї. –Ю–Ї–∞–Ј–∞–ї–Њ—Б—М, —З—В–Њ —В—А–∞–µ–Ї—В–Њ—А–Є—П –і–≤–Є–ґ–µ–љ–Є—П —Б–≤–Њ–±–Њ–і–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –Є –ї—Г—З —Б–≤–µ—В–∞ —П–≤–ї—П—О—В—Б—П —Н–Ї—Б—В—А–µ–Љ–∞–ї—П–Љ–Є –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –Њ–і–љ–Њ–≥–Њ –Є —В–Њ–≥–Њ –ґ–µ —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–∞ –і–µ–є—Б—В–≤–Є—П. –Ф–∞–љ–љ–Њ–µ –Њ–±—Б—В–Њ—П—В–µ–ї—М—Б—В–≤–Њ –љ–∞—В–Њ–ї–Ї–љ—Г–ї–Њ –Ы—Г–Є –і–µ –С—А–Њ–є–ї—П –љ–∞ –Љ—Л—Б–ї—М, —З—В–Њ –µ—Б–ї–Є –≤–Њ–ї–љ–µ, –Њ–њ–Є—Б—Л–≤–∞–µ–Љ–Њ–є —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ
w = exp{i(V t вАУ kr)}, (2)
–≥–і–µ V –Є k вАУ —З–∞—Б—В–Њ—В–∞ –Є –≤–Њ–ї–љ–Њ–≤–Њ–є –≤–µ–Ї—В–Њ—А —Н–ї–µ–Ї—В—А–Њ–Љ–∞–≥–љ–Є—В–љ–Њ–є –≤–Њ–ї–љ—Л;
t вАУ –≤—А–µ–Љ—П;
r вАУ –≤–µ–Ї—В–Њ—А, –Ј–∞–і–∞—О—Й–Є–є –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –µ–µ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П,
–њ—А–Є—Б—Г—Й–Є –љ–µ–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ —З–∞—Б—В–Є—Ж—Л - —Д–Њ—В–Њ–љ–∞ (—В. –µ. –Ї–Њ—А–њ—Г—Б–Ї—Г–ї—П—А–љ—Л–µ —Б–≤–Њ–є—Б—В–≤–∞), —В–Њ –≤–њ–Њ–ї–љ–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ —Б–Є–Љ–Љ–µ—В—А–Є–Є, —В. –µ. –і–≤–Є–ґ—Г—Й–µ–є—Б—П –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —З–∞—Б—В–Є—Ж–µ –Љ–Њ–ґ–µ—В —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞—В—М –љ–µ–Ї–∞—П –њ–ї–Њ—Б–Ї–∞—П –≤–Њ–ї–љ–∞ –Љ–∞—В–µ—А–Є–Є
ќ® = exp{i(Et вАУ pr)/ƒІ}, (3)
–≥–і–µ –Х вАУ –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П –і–≤–Є–ґ—Г—Й–µ–є—Б—П —З–∞—Б—В–Є—Ж—Л,
—А = mv вАУ –µ–µ –Є–Љ–њ—Г–ї—М—Б.
–Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –Ы—Г–Є –і–µ –С—А–Њ–є–ї—М –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є–ї,
—З—В–Њ –ї—О–±–Њ–є –і–≤–Є–ґ—Г—Й–µ–є—Б—П —З–∞—Б—В–Є—Ж–µ –Љ–Њ–ґ–љ–Њ
–њ–Њ—Б—В–∞–≤–Є—В—М –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –≤–Њ–ї–љ—Г —Б —З–∞—Б—В–Њ—В–Њ–є
пБЈ = E/пБ®
–Є –і–ї–Є–љ–Њ–є –≤–Њ–ї–љ—Л пБђ
= 2пБ∞ пБ®
/p. –≠—В–∞ –Є–і–µ—П –Њ–Ї–∞–Ј–∞–ї–∞—Б—М
–љ–µ —В–Њ–ї—М–Ї–Њ –ї–Њ–≥–Є—З–µ—Б–Ї–Є –Ї—А–∞—Б–Є–≤–Њ–є, –љ–Њ –Є
–њ—А–Њ–і—Г–Ї—В–Є–≤–љ–Њ–є. –Т 1929 –≥.
–Ю. –®—В–µ—А–љ –Є –Ш.
–≠—Б—В–µ—А–Љ–∞–љ –њ–Њ–Ї–∞–Ј–∞–ї–Є, —З—В–Њ –Є–і–µ—П —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П
–≤–Њ–ї–љ –Љ–∞—В–µ—А–Є–Є, –њ—А–µ–і–ї–Њ–ґ–µ–љ–љ–∞—П –і–µ –С—А–Њ–є–ї–µ–Љ,
–њ—А–Є–Љ–µ–љ–Є–Љ–∞ –і–ї—П –Њ–њ–Є—Б–∞–љ–Є—П —П–≤–ї–µ–љ–Є—П –і–Є—Д—А–∞–Ї—Ж–Є–Є
–∞—В–Њ–Љ–Њ–≤ –љ–∞ –Ї—А–Є—Б—В–∞–ї–ї–Є—З–µ—Б–Ї–Є—Е —А–µ—И–µ—В–Ї–∞—Е
–Ї—А–Є—Б—В–∞–ї–ї–Њ–≤.
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –≤ –Њ–і–љ–Њ–є –Є–Ј —А–∞–љ–љ–Є—Е —А–∞–±–Њ—В –≠—А–≤–Є–љ –®—А–µ–і–Є–љ–≥–µ—А, –Ї—А–Є—В–Є—З–µ—Б–Ї–Є –Њ—В–љ–Њ—Б—П—Б—М –Ї —Б—В–∞—В–Є—Б—В–Є–Ї–µ –С–Њ–Ј–µ вАУ –≠–є–љ—И—В–µ–є–љ–∞, –Ј–∞–і–∞–ї—Б—П –≤–Њ–њ—А–Њ—Б–Њ–Љ: вАУ ¬Ђ–Я–Њ—З–µ–Љ—Г –±—Л –љ–µ –љ–∞—З–∞—В—М —Б –≤–Њ–ї–љ–Њ–≤–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —З–∞—Б—В–Є—Ж –≥–∞–Ј–∞, –∞ –Ј–∞—В–µ–Љ –љ–∞–ї–Њ–ґ–Є—В—М –љ–∞ —В–∞–Ї–Є–µ ¬Ђ–≤–Њ–ї–љ—Л¬ї —Г—Б–ї–Њ–≤–Є—П –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П ¬Ђ–∞ –ї—П —Г—Б–ї–Њ–≤–Є–µ –Ф–µ–±–∞—П¬ї? –Я–Њ—Б–ї–µ —З–µ–≥–Њ —Б–ї–µ–і—Г–µ—В –Ї–ї—О—З–µ–≤–∞—П –Є–і–µ—П: вАУ ¬Ђ–≠—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В –љ–µ —З—В–Њ –Є–љ–Њ–µ, –Ї–∞–Ї –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М —Б–µ—А—М–µ–Ј–љ–Њ –Њ—В–љ–µ—Б—В–Є—Б—М –Ї –њ—А–µ–і–ї–Њ–ґ–µ–љ–љ–Њ–є –Ы. –і–µ –С—А–Њ–є–ї–µ–Љ –Є –Р. –≠–є–љ—И—В–µ–є–љ–Њ–Љ –≤–Њ–ї–љ–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –і–≤–Є–ґ—Г—Й–Є—Е—Б—П —З–∞—Б—В–Є—Ж¬ї.
–°–ї–µ–і—Г—О—Й–∞—П —Б—В–∞—В—М—П –®—А–µ–і–Є–љ–≥–µ—А–∞ —Г–ґ–µ —Б–Њ–і–µ—А–ґ–∞–ї–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ (1), –њ–Њ–ї–Њ–ґ–Є–≤—И–µ–µ –љ–∞—З–∞–ї–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ, –љ–∞—А—П–і—Г —Б –њ–Є–Њ–љ–µ—А—Б–Ї–Є–Љ–Є —А–∞–±–Њ—В–∞–Љ–Є –Ь–∞–Ї—Б–∞ –Я–ї–∞–љ–Ї–∞, –Р–ї—М–±–µ—А—В–∞ –≠–є–љ—И—В–µ–є–љ–∞, –Э–Є–ї—М—Б–∞ –С–Њ—А–∞ –Є –Т–µ—А–љ–µ—А–∞ –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞.
–Ф–Њ–≤–Њ–і—Л, –њ—А–Є–≤–µ–і–µ–љ–љ—Л–µ –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –њ—А–Є –≤—Л–≤–Њ–і–µ —Г—А–∞–≤–љ–µ–љ–Є—П (1), –≤–њ–Њ—Б–ї–µ–і—Б—В–≤–Є–Є –±—Л–ї–Є –њ—А–Є–Ј–љ–∞–љ—Л —Б–њ–µ—Ж–Є–∞–ї–Є—Б—В–∞–Љ–Є –љ–µ–≤–µ—А–љ—Л–Љ–Є, –Њ–і–љ–∞–Ї–Њ —Б–∞–Љ–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Њ–Ї–∞–Ј–∞–ї–Њ—Б—М –≤–µ—А–љ—Л–Љ. –≠—В–Њ –љ–µ –µ–і–Є–љ—Б—В–≤–µ–љ–љ—Л–є —Б–ї—Г—З–∞–є –≤ –љ–∞—Г–Ї–µ. –Э–∞–њ—А–Є–Љ–µ—А, –Њ—Б–љ–Њ–≤–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П —Н–ї–µ–Ї—В—А–Њ–і–Є–љ–∞–Љ–Є–Ї–Є —В–∞–Ї–ґ–µ –±—Л–ї–Є –њ–Њ–ї—Г—З–µ–љ—Л –Ф–ґ–µ–є–Љ—Б–Њ–Љ –Ъ–ї–µ—А–Ї–Њ–Љ –Ь–∞–Ї—Б–≤–µ–ї–ї–Њ–Љ –Є–Ј –љ–µ–≤–µ—А–љ—Л—Е –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–є –Њ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є—Е —Б–≤–Њ–є—Б—В–≤–∞—Е —Н—Д–Є—А–∞.
–Ч–љ–∞—З–Є—В–µ–ї—М–љ–Њ –њ–Њ–Ј–ґ–µ –±—Л–ї–Њ —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ–Њ, —З—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ (1) –њ–Њ–ї—Г—З–∞–µ—В—Б—П –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —Б–ї–µ–і—Г—О—Й–µ–є —Д–Њ—А–Љ–∞–ї—М–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є –њ—А–Њ—Ж–µ–і—Г—А—Л. –Я–Њ–ї–љ–∞—П –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П –Х –љ–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є —З–∞—Б—В–Є—Ж—Л –≤ –љ–µ–Ї–Њ–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–Љ –њ–Њ–ї–µ U(r,t) —А–∞–≤–љ–∞
(4)
–≥–і–µ —А вАУ –Є–Љ–њ—Г–ї—М—Б —З–∞—Б—В–Є—Ж—Л,
r вАУ –≤–µ–Ї—В–Њ—А, –Ј–∞–і–∞—О—Й–Є–є –µ–µ –Љ–µ—Б—В–Њ–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –≤ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–Љ –њ–Њ–ї–µ,
t вАУ –≤—А–µ–Љ—П.
–Ч–∞–Љ–µ–љ—П—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є (4) —Д–Є–Ј–Є—З–µ—Б–Ї–Є–µ –≤–µ–ї–Є—З–Є–љ—Л –љ–∞ –Њ–њ–µ—А–∞—В–Њ—А—Л:
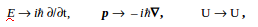 ,
(5)
,
(5)
–≥–і–µ
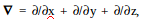 ,
–њ—А–Є –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–µ —Н—В–Є—Е –Њ–њ–µ—А–∞—В–Њ—А–Њ–≤ –≤
–≤—Л—А–∞–ґ–µ–љ–Є–µ (4) –Є —Г–Љ–љ–Њ–ґ–µ–љ–Є–Є –µ–≥–Њ —Б–њ—А–∞–≤–∞ –љ–∞
пБЩ
- —Д—Г–љ–Ї—Ж–Є—О, –њ–Њ–ї—Г—З–∞–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞
(1):
,
–њ—А–Є –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–µ —Н—В–Є—Е –Њ–њ–µ—А–∞—В–Њ—А–Њ–≤ –≤
–≤—Л—А–∞–ґ–µ–љ–Є–µ (4) –Є —Г–Љ–љ–Њ–ґ–µ–љ–Є–Є –µ–≥–Њ —Б–њ—А–∞–≤–∞ –љ–∞
пБЩ
- —Д—Г–љ–Ї—Ж–Є—О, –њ–Њ–ї—Г—З–∞–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞
(1):
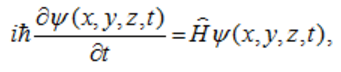 (6)
(6)
–≥–і–µ
![]() вАУ –Њ–њ–µ—А–∞—В–Њ—А, –њ–Њ–ї—Г—З–Є–≤—И–Є–є –љ–∞–Ј–≤–∞–љ–Є–µ
–≥–∞–Љ–Є–ї—М—В–Њ–љ–Є–∞–љ–∞ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л.
–Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ —Б—В—А–Њ—П—В—Б—П –≤—Б–µ
–Њ–њ–µ—А–∞—В–Њ—А—Л –Ї–≤–∞–љ—В–Њ–≤—Л—Е —В–µ–Њ—А–Є–є.
вАУ –Њ–њ–µ—А–∞—В–Њ—А, –њ–Њ–ї—Г—З–Є–≤—И–Є–є –љ–∞–Ј–≤–∞–љ–Є–µ
–≥–∞–Љ–Є–ї—М—В–Њ–љ–Є–∞–љ–∞ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л.
–Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ —Б—В—А–Њ—П—В—Б—П –≤—Б–µ
–Њ–њ–µ—А–∞—В–Њ—А—Л –Ї–≤–∞–љ—В–Њ–≤—Л—Е —В–µ–Њ—А–Є–є.
–Ф–∞–љ–љ—Л–є —А–µ—Ж–µ–њ—В—Г—А–љ—Л–є —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Њ–Ї—Г—В—Л–≤–∞–µ—В —Б—Г—В—М –њ—А–Њ–Є—Б—Е–Њ–і—П—Й–µ–≥–Њ –≤ –Љ–Є–Ї—А–Њ–Љ–Є—А–µ –Є–љ—В–µ–ї–ї–µ–Ї—В—Г–∞–ї—М–љ—Л–Љ —В—Г–Љ–∞–љ–Њ–Љ, –њ–Њ–ї–љ–Њ—Б—В—М—О –Њ—В–Њ—А–≤–∞–љ–љ—Л–Љ –Њ—В —А–µ–∞–ї—М–љ–Њ—Б—В–Є. –І–Є—Б–ї–µ–љ–љ—Л–µ –Љ–µ—В–Њ–і—Л, —А–∞–Ј–≤–Є—В—Л–µ –љ–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В–∞–Љ–Є, –±—Л–ї–Є –љ–∞—Ж–µ–ї–µ–љ—Л –љ–µ –љ–∞ –њ–Њ—Б—В–Є–ґ–µ–љ–Є–µ —Б—Г—В–Є —П–≤–ї–µ–љ–Є–є –≤ –Љ–Є–Ї—А–Њ–Љ–Є—А–µ, –∞ –љ–∞ —Б–Њ–њ–Њ—Б—В–∞–≤–ї–µ–љ–Є–µ —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ —А–∞—Б—З–µ—В–Њ–≤ —Б —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є –і–∞–љ–љ—Л–Љ–Є. –Э–∞–і–Њ –≤—Л—А–∞–Ј–Є—В—М –Є–Љ –≥–ї—Г–±–Њ–Ї–Њ–µ –њ–Њ—З—В–µ–љ–Є–µ, –Є–±–Њ –Њ–љ–Є —П–≤–Є–ї–Є —В–Њ—А–ґ–µ—Б—В–≤–Њ —З–µ–ї–Њ–≤–µ—З–µ—Б–Ї–Њ–є –Љ—Л—Б–ї–Є –љ–∞ —А—Г–±–µ–ґ–∞—Е –Љ–µ–ґ–і—Г –њ–Њ–Ј–љ–∞–љ–љ—Л–Љ –Є –љ–µ–њ–Њ–Ј–љ–∞–љ–љ—Л–Љ. –Э–Њ –љ–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В—Л –≤–Њ–Ј–≤–µ–ї–Є –Њ—В–ї–Є—З–Є–µ –Ї–≤–∞–љ—В–Њ–≤—Л—Е —П–≤–ї–µ–љ–Є–є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞ –Њ—В —Б–≤–Њ–є—Б—В–≤ –љ–∞–±–ї—О–і–∞–µ–Љ–Њ–є —А–µ–∞–ї—М–љ–Њ—Б—В–Є –≤ —Д–Є–ї–Њ—Б–Њ—Д—Б–Ї–Є–є –њ—А–Є–љ—Ж–Є–њ: - ¬Ђ–Э–µ–Ј–љ–∞–µ–Љ, –Є –љ–µ —Г–Ј–љ–∞–µ–Љ¬ї. –≠—В–Њ, –љ–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і, –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ –њ–Њ–≤–ї–Є—П–ї–Њ –љ–∞ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–Њ–Ї–Њ–ї–µ–љ–Є–є —Д–Є–Ј–Є–Ї–Њ–≤.
–Ґ–Њ, —З—В–Њ —А–µ–Ј—Г–ї—М—В–∞—В—Л —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ –њ–Њ —А–∞—Б—Б–µ—П–љ–Є—О —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж —Г–і–∞–ї–Њ—Б—М –Њ–±—К—П—Б–љ–Є—В—М —Б –њ–Њ–Љ–Њ—Й—М—О –≤–Њ–ї–љ –Љ–∞—В–µ—А–Є–Є –і–µ –С—А–Њ–є–ї—П вАУ —Н—В–Њ —З—Г–і–Њ, —В. –Ї. —Н—В–Њ –љ–µ —А–µ–Ј—Г–ї—М—В–∞—В –і–µ—В–∞–ї—М–љ–Њ–≥–Њ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –Љ–Є–Ї—А–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ —А–∞—Б—Б–µ—П–љ–Є—П —З–∞—Б—В–Є—Ж –љ–∞ –∞—В–Њ–Љ–љ—Л—Е –Ї—А–Є—Б—В–∞–ї–ї–Є—З–µ—Б–Ї–Є—Е —А–µ—И–µ—В–Ї–∞—Е, –∞ –њ—А–Њ—Б—В–Њ —Д–µ–љ–Њ–Љ–µ–љ–∞–ї—М–љ–Њ–µ —Б–Њ–≤–њ–∞–і–µ–љ–Є–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ–≥–Њ —Д–∞–Ї—В–∞ —Б –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ–є –Є–і–µ–µ–є. –Ъ–∞–Ї –±—Л —В–∞–Љ –љ–Є –±—Л–ї–Њ, –љ–Њ –Є–Љ–µ–љ–љ–Њ —Н—В–Њ —Б–Њ–≤–њ–∞–і–µ–љ–Є–µ –њ—А–Є–≤–µ–ї–Њ –Ї —А–∞–Ј–≤–Є—В–Є—О –Ї–Њ—А–њ—Г—Б–Ї—Г–ї—П—А–љ–Њ-–≤–Њ–ї–љ–Њ–≤–Њ–≥–Њ –і—Г–∞–ї–Є–Ј–Љ–∞ –Є, –≤ –Є—В–Њ–≥–µ, –Ї —Б–Њ–Ј–і–∞–љ–Є—О вАУ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є.
–Ч–∞ –і–µ–≤—П–љ–Њ—Б—В–Њ –ї–µ—В, –њ—А–Њ—И–µ–і—И–Є—Е —Б 1926 –≥–Њ–і–∞ –Љ–љ–Њ–≥–Њ –Є—Б—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–µ–є –њ—А–µ–і–ї–∞–≥–∞–ї–Є —А–∞–Ј–ї–Є—З–љ—Л–µ —Б–њ–Њ—Б–Њ–±—Л –≤—Л–≤–Њ–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–є –®—А–µ–і–Є–љ–≥–µ—А–∞. –Э–Њ, –љ–∞—Б–Ї–Њ–ї—М–Ї–Њ –Љ–љ–µ –Є–Ј–≤–µ—Б—В–љ–Њ, –љ–µ –Њ–і–љ–∞ –Є–Ј —Н—В–Є—Е –њ–Њ–њ—Л—В–Њ–Ї –љ–µ —Г–≤–µ–љ—З–∞–ї–∞—Б—М —Г—Б–њ–µ—Е–Њ–Љ. –Ю—Б–љ–Њ–≤—Л –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Є –њ–Њ —Б–µ–є –і–µ–љ—М –≤—Л–Ј—Л–≤–∞—О—В –і–Є—Б–Ї—Г—Б—Б–Є–Є –≤ –љ–∞—Г—З–љ–Њ–Љ —Б–Њ–Њ–±—Й–µ—Б—В–≤–µ.
–Т—Л—А–∞–±–Њ—В–∞–љ–љ—Л–є –≤ –Ъ–Њ–њ–µ–љ–≥–∞–≥–µ–љ–µ –µ—Й–µ –≤ –љ–∞—З–∞–ї–µ –њ—А–Њ—И–ї–Њ–≥–Њ –≤–µ–Ї–∞ –Ї–Њ–љ—Ж–µ–њ—В—Г–∞–ї—М–љ—Л–є –њ–Њ–і—Е–Њ–і, –≤—Л—А–∞–ґ–µ–љ–љ—Л–є –≤ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ–Њ–є –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–Є –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є пБє (x,y,z,t) –Є —А–∞–Ј–≤–Є—В—Л–є –љ–∞ —Н—В–Њ–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–є —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –њ–Њ–ї–љ–Њ—Б—В—М—О –Є—Б–Ї–ї—О—З–∞–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –ї—О–±–Њ–≥–Њ –њ—А–Є—З–Є–љ–љ–Њ–≥–Њ –Њ–њ–Є—Б–∞–љ–Є—П —П–≤–ї–µ–љ–Є–є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞. –Э–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В—Л, —Б–Њ–Ј–і–∞–≤—И–Є–µ –Є –≤–Њ–Ј–≥–ї–∞–≤–Є–≤—И–Є–µ –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ, –љ–∞—Б—В–Њ—П–ї–Є –љ–∞ —В–Њ–Љ, —З—В–Њ –љ–∞ –њ–Є–Ї–Њ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Њ–Љ (пБЊ10вАУ11вА¶10вАУ13 —Б–Љ) —Г—А–Њ–≤–љ–µ –Њ—А–≥–∞–љ–Є–Ј–∞—Ж–Є–Є –Љ–∞—В–µ—А–Є–Є –і–µ—В–µ—А–Љ–Є–љ–Є–Ј–Љ –њ–Њ–ї–љ–Њ—Б—В—М—О —Г—Б—В—Г–њ–∞–µ—В –Љ–µ—Б—В–Њ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ–Њ–Љ—Г —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ—Г. –Ы—О–±–Њ–µ —Г–њ–Њ–Љ–Є–љ–∞–љ–Є–µ –Њ —В—А–∞–µ–Ї—В–Њ—А–Є–Є –і–≤–Є–ґ–µ–љ–Є—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж –Є –Є—Е —А–∞–Ј–Љ–µ—А–∞—Е –≤—Л—Е–Њ–і–Є—В –Ј–∞ —А–∞–Љ–Ї–Є –љ–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В—Б–Ї–Є—Е –≤–Њ–Ј–Ј—А–µ–љ–Є–є, —З—В–Њ –≤–љ–∞—З–∞–ї–µ –њ–Њ—Б–ї—Г–ґ–Є–ї–Њ –Ї–Њ–ї–Њ—Б—Б–∞–ї—М–љ–Њ–Љ—Г –њ—А–Њ–≥—А–µ—Б—Б—Г –≤ —А–∞–Ј–≤–Є—В–Є–Є –Ї–≤–∞–љ—В–Њ–≤—Л—Е —В–µ–Њ—А–Є–є, –∞ —В–µ–њ–µ—А—М, –љ–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і, —П–≤–ї—П–µ—В—Б—П –њ—А–µ–њ—П—В—Б—В–≤–Є–µ–Љ –љ–∞ –њ—Г—В–Є —А–∞–Ј–≤–Є—В–Є—П –љ–∞—И–Є—Е –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є –Њ –≥–ї—Г–±–Є–љ–∞—Е –Љ–Є—А–Њ–Ј–і–∞–љ–Є—П.
–Ы–Њ–≥–Є—З–µ—Б–Ї–∞—П –љ–µ–Ј–∞–≤–µ—А—И–µ–љ–љ–Њ—Б—В—М –Њ—Б–љ–Њ–≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –≤—Л–Ј—Л–≤–∞–ї–∞ –і—Г—И–µ–≤–љ—Л–є –і–Є—Б–Ї–Њ–Љ—Д–Њ—А—В –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤—Б–µ—Е —Г –µ–µ —Б–Њ–Ј–і–∞—В–µ–ї–µ–є: –Ь–∞–Ї—Б–∞ –Я–ї–∞–љ–Ї–∞, –Ы—Г–Є –і–µ –С—А–Њ–є–ї—П, –Р–ї—М–±–µ—А—В–∞ –≠–є–љ—И—В–µ–є–љ–∞, –≠—А–≤–Є–љ–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞. –Т—Б–µ –Њ–љ–Є –њ–Њ–ї–∞–≥–∞–ї–Є, —З—В–Њ –Ї–≤–∞–љ—В–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ –ї–Є—И—М –њ—А–µ–ї—О–і–Є—П –њ–µ—А–µ–і –±—Г–і—Г—Й–µ–є, –≤–µ—А–љ–Њ–є —В–µ–Њ—А–Є–µ–є. –Ш–Љ –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ –≤–Њ–Ј—А–∞–ґ–∞–ї –ї–Є—И—М –Э–Є–ї—М—Б –С–Њ—А, —Г—В–≤–µ—А–ґ–і–∞–≤—И–Є–є: вАУ ¬Ђ–Т—Б–µ —Б–Њ–≥–ї–∞—Б–љ—Л, —З—В–Њ –љ–∞—И–∞ —В–µ–Њ—А–Є—П –±–µ–Ј—Г–Љ–љ–∞. –Ь—Л —А–∞—Б—Е–Њ–і–Є–Љ—Б—П –ї–Є—И—М –≤ –Њ–і–љ–Њ–Љ: –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –ї–Є –Њ–љ–∞ –±–µ–Ј—Г–Љ–љ–∞?¬ї. –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ, —В—А—Г–і–љ–Њ –Њ—Б–Њ–Ј–љ–∞—В—М, —З—В–Њ —Г –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –љ–µ—В —А–∞–Ј–Љ–µ—А–Њ–≤ –Є —В—А–∞–µ–Ї—В–Њ—А–Є–Є –і–≤–Є–ґ–µ–љ–Є—П, —В–µ–Љ –љ–µ –Љ–µ–љ–µ–µ, –Ї–Њ–њ–µ–љ–≥–∞–≥–µ–љ—Б–Ї–Њ–є —И–Ї–Њ–ї–µ —Г–і–∞–ї–Њ—Б—М —Г–±–µ–і–Є—В—М –≤ —Н—В–Њ–Љ –≤—Б–µ —Ж–Є–≤–Є–ї–Є–Ј–Њ–≤–∞–љ–љ–Њ–µ —З–µ–ї–Њ–≤–µ—З–µ—Б—В–≤–Њ.
–®–Ї–Њ–ї–∞ –Э. –С–Њ—А–∞ –Њ–і–µ—А–ґ–∞–ї–∞ –≤ –љ–∞—З–∞–ї–µ 20-–≥–Њ –≤–µ–Ї–∞ ¬Ђ–њ–Є—А—А–Њ–≤—Г¬ї –њ–Њ–±–µ–і—Г –±–ї–∞–≥–Њ–і–∞—А—П –±–ї–Є—Б—В–∞—В–µ–ї—М–љ–Њ–є –њ–ї–µ—П–і–µ –µ–≥–Њ —Г—З–µ–љ–Є–Ї–Њ–≤ –Є –µ–і–Є–љ–Њ–Љ—Л—И–ї–µ–љ–љ–Є–Ї–Њ–≤: –У–µ–є–Ј–µ–љ–±–µ—А—Г, –Щ–Њ—А–і–∞–љ—Г, –С–Њ—А–љ—Г, –Я–∞—Г–ї–Є, –Ф–Є—А–∞–Ї—Г –Є –Љ–љ–Њ–≥–Є—Е –і—А—Г–≥–Є—Е –Є—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–µ–є. –≠—В–Њ –њ–Њ–Ї–Њ–ї–µ–љ–Є–µ —Г—З–µ–љ—Л—Е –ї–µ–≥–Ї–Њ ¬Ђ—Б–Ї–Є–љ—Г–ї–Њ¬ї —Б —Б–µ–±—П –Љ–µ–љ—В–∞–ї—М–љ—Л–є –≥—А—Г–Ј –і–µ—В–µ—А–Љ–Є–љ–Є—Б—В—Б–Ї–Є—Е –≤–Њ–Ј–Ј—А–µ–љ–Є–є. –Ю–љ–Є –±–µ–Ј –Њ—Б–Њ–±—Л—Е –і—Г—И–µ–≤–љ—Л—Е —В–µ—А–Ј–∞–љ–Є–є, –ї–µ–≥–Ї–Њ –Њ–±–Љ–µ–љ—П–ї–Є ¬Ђ–Ј–і—А–∞–≤—Л–є —Б–Љ—Л—Б–ї¬ї (—В.–µ. –љ–∞–≥–ї—П–і–љ—Г—О —Д–Є–Ј–Є–Ї—Г) –љ–∞ —А–µ—Ж–µ–њ—В—Г—А–љ—Л–є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ. –° —В–µ—Е –њ–Њ—А –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є –Ї–Њ–њ–µ–љ–≥–∞–≥–µ–љ—Б–Ї–Њ–є —И–Ї–Њ–ї—Л —Б –њ–µ—А–µ–Љ–µ–љ–љ—Л–Љ–Є —Г—Б–њ–µ—Е–∞–Љ–Є –њ—Л—В–∞—О—В—Б—П –і–≤–∞–ґ–і—Л –њ—А–Њ–Ї–≤–∞–љ—В–Њ–≤–∞—В—М –≤—Б–µ –≤–Є–і—Л –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є–є, —З—В–Њ–±—Л –≤ –Є—В–Њ–≥–µ —А–∞—Б—Б—З–Є—В–∞—В—М –≤—Б–µ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л (–∞–Љ–њ–ї–Є—В—Г–і—Л) —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ–Њ–є S-–Љ–∞—В—А–Є—Ж—Л. –Я—А–Є —Н—В–Њ–Љ –Њ–љ–Є –љ–µ –Њ—Б–Њ–±–Њ –Ј–∞–±–Њ—В—П—В—Б—П –Њ –љ–∞–≥–ї—П–і–љ–Њ—Б—В–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е –Љ–Њ–і–µ–ї–µ–є, –∞ —Ж–µ–њ–ї—П—О—В—Б—П –Ј–∞ –Љ–Њ—Й–љ—Л–є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –∞–њ–њ–∞—А–∞—В —В–µ–Њ—А–Є–Є –≥—А—Г–њ–њ.
–†–∞–Ј–≤–Є–≤–∞–µ–Љ—Л–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞–Љ–Є ¬Ђ—Б—В—А—Г–љ–љ—Л–µ¬ї –≤–Њ–Ј–Ј—А–µ–љ–Є—П, –љ–µ—Б–Њ–Љ–љ–µ–љ–љ–Њ, –њ–Њ–ї–µ–Ј–љ—Л –і–ї—П —А–∞—Б—И–Є—А–µ–љ–Є—П –ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є –Њ—Б–љ–∞—Й–µ–љ–љ–Њ—Б—В–Є —З–µ–ї–Њ–≤–µ—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б—Б—Г–і–Ї–∞. –Т –Ї–Њ–љ—Ж–µ –Ї–Њ–љ—Ж–Њ–≤, –Є—Е —В—А—Г–і—Л –њ—А–Є–љ–µ—Б—Г—В ¬Ђ–Ј–Њ–ї–Њ—В—Л–µ¬ї –њ–ї–Њ–і—Л. –Э–Њ ¬Ђ—Б—В—А—Г–љ–љ–∞—П¬ї –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞, –Њ—В–Њ—А–≤–∞–љ–љ–∞—П –Њ—В —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є, —Б–ї–Є—И–Ї–Њ–Љ –Є–Ј–±—Л—В–Њ—З–љ–∞, —З—В–Њ–±—Л —Б—А–µ–і–Є –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–≥–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ –њ—А–µ–і–ї–∞–≥–∞–µ–Љ—Л—Е –µ—О –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–µ–є, –Є—Б—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є –Љ–Њ–≥–ї–Є –љ–∞—Й—Г–њ–∞—В—М –µ–і–Є–љ—Б—В–≤–µ–љ–љ—Г—О –њ—Г—В–µ–≤–Њ–і–љ—Г—О ¬Ђ–љ–Є—В—М¬ї.
–С–µ–Ј–і–љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–µ–є –±–µ–Ј–љ–∞–і–µ–ґ–љ–Њ –Њ—Б–ї–Њ–ґ–љ—П–µ—В –њ–Њ–Є—Б–Ї–Є ¬Ђ–Є—Б—В–Є–љ–љ–Њ–≥–Њ –≤–∞–Ї—Г—Г–Љ–∞¬ї, –њ–Њ—Н—В–Њ–Љ—Г –±–Њ–ї—М—И–Є–љ—Б—В–≤–Њ —Б—В—А—Г–љ–љ—Л—Е —В–µ–Њ—А–µ—В–Є–Ї–Њ–≤ –њ—А–Њ–і–Њ–ї–ґ–∞—О—В –Ј–∞—В—А–∞—З–Є–≤–∞—В—М –Ї–Њ–ї–Њ—Б—Б–∞–ї—М–љ—Л–µ —Г—Б–Є–ї–Є—П –љ–∞ –њ–Њ–Є—Б–Ї–Є –≤–∞—А–Є–∞–љ—В–Њ–≤ —Г—Б—В—А–∞–љ–µ–љ–Є—П —А–∞—Б—Е–Њ–і–Є–Љ–Њ—Б—В–µ–є (–±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–µ–є), –і—Г—Е–Њ–≤ (–Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л—Е –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є) –Є —В–∞—Е–Є–Њ–љ–Њ–≤ (–љ–µ—Б—В–∞–±–Є–ї—М–љ–Њ—Б—В–µ–є –≤–∞–Ї—Г—Г–Љ–∞) –≤ –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е –Ї–≤–∞–љ—В–Њ–≤—Л—Е —В–µ–Њ—А–Є—П—Е, –∞ –љ–µ –њ—Л—В–∞—О—В—Б—П –≤–Њ—Б—Б–Њ–Ј–і–∞–≤–∞—В—М –љ–∞–≥–ї—П–і–љ—Л–µ –Љ–Њ–і–µ–ї–Є –Њ–±–Є—В–∞—В–µ–ї–µ–є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞. –Я–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –Ї–Њ—В–Њ—А—Л–µ –Ј–∞–Љ–µ—В–∞—О—В —Б—Г–њ–µ—А—Б—В—А—Г–љ—Л –≤ 10-–Љ–µ—А–љ—Л—Е –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є—П—Е –Ъ–∞–ї–∞–±–Є - –ѓ—Г, —Б—В—А—Г–љ—Л –≤ 26-–Љ–µ—А–љ—Л—Е –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞—Е –Є —А-–±—А–∞–љ—Л, –Ї–Њ–љ–µ—З–љ–Њ –Њ–±–ї–∞–і–∞—О—В —Н–ї–µ–Љ–µ–љ—В–∞–Љ–Є –љ–∞–≥–ї—П–і–љ–Њ—Б—В–Є, –Є —Н—В–Њ –њ—А–Є–≤–Є–ї–Њ –Ї –Њ—Й—Г—В–Є–Љ–Њ–Љ—Г –њ—А–Њ–≥—А–µ—Б—Б—Г —Б—В—А—Г–љ–љ—Л—Е —В–µ–Њ—А–Є–є. –Э–Њ (–љ–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і) –Є—Б—Е–Њ–і–љ–∞—П –ї–Њ–≥–Є—З–µ—Б–Ї–∞—П –љ–µ–Ј–∞–≤–µ—А—И–µ–љ–љ–Њ—Б—В—М –Њ—Б–љ–Њ–≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Д–Є–Ј–Є–Ї–Є –Є –Њ–±—Й–µ–є —В–µ–Њ—А–Є–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є –Љ–µ—И–∞–µ—В —А–∞–Ј–≤–Є—В–Є—О —Б—В—А—Г–љ–љ—Л—Е –≤–Њ–Ј–Ј—А–µ–љ–Є–є.
–Ф–ї—П –≤—Л—Е–Њ–і–∞ –Є–Ј —Б–ї–Њ–ґ–Є–≤—И–µ–є—Б—П –≤ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є —Д–Є–Ј–Є–Ї–µ –Љ–Є–Ї—А–Њ–Љ–Є—А–∞ —Б–Є—В—Г–∞—Ж–Є–Є, –љ–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ–њ–µ—А–µ—В—М—Б—П –љ–∞ –љ–∞–≥–ї—П–і–љ—Л–µ –Љ–Њ–і–µ–ї–Є —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж (—А–∞–Ј–≤–Є–≤–∞–µ–Љ—Л–µ, –љ–∞–њ—А–Є–Љ–µ—А, –≤ –Р–ї–≥–µ–±—А–µ —Б–Є–≥–љ–∞—В—Г—А [2,3,4]), –∞ —В–∞–Ї –ґ–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ—А–Њ–Є–Ј–≤–µ—Б—В–Є —А–µ–≤–Є–Ј–Є—О –ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е –Њ—Б–љ–Њ–≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Ш–Љ–µ–µ–Љ–Њ —Н—В–Њ–є –њ—А–Њ–±–ї–µ–Љ–µ –Є –њ–Њ—Б–≤—П—Й–µ–љ–∞ –љ–Є–ґ–µ–Є–Ј–ї–Њ–ґ–µ–љ–љ–∞—П —Б—В–∞—В—М—П.
–Я—А–µ–і–ї–Њ–ґ–µ–љ–љ–∞—П –Ј–і–µ—Б—М –Љ–Њ–і–µ–ї—М –±–ї—Г–ґ–і–∞—О—Й–µ–є —З–∞—Б—В–Є—Ж—Л (–Њ–±–ї–∞–і–∞—О—Й–µ–є –Њ–±—К–µ–Љ–Њ–Љ –Є —Е–∞–Њ—В–Є—З–љ–Њ–є —В—А–∞–µ–Ї—В–Њ—А–Є–µ–є –і–≤–Є–ґ–µ–љ–Є—П), —П–≤–љ–Њ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В –љ–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В—Б–Ї–Є–Љ –≤–Њ–Ј–Ј—А–µ–љ–Є—П–Љ, –љ–Њ –њ—А–Є–≤–Њ–і–Є—В –Ї –≤—Л–≤–Њ–і—Г —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞.
2
–†–Є—Б.1. –І–∞—Б—В–Є—Ж–∞ (–Љ–∞—В–µ—А–Є–∞–ї—М–љ–∞—П ¬Ђ—В–Њ—З–Ї–∞¬ї),
—Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –±–ї—Г–ґ–і–∞—О—Й–∞—П –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є
—Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ
–µ–µ –њ–Њ–ї–љ–∞—П –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П E
–≤—Б–µ–≥–і–∞ –Њ—Б—В–∞–µ—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є (–Х = const)
. –Ь–Њ–і–µ–ї—М –±–ї—Г–ґ–і–∞—О—Й–µ–є —З–∞—Б—В–Є—Ж—Л–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–∞—Б—В–Є—Ж—Г, –Њ–±–ї–∞–і–∞—О—Й—Г—О –Љ–∞—Б—Б–Њ–є m –Є –љ–µ–±–Њ–ї—М—И–Є–Љ –Њ–±—К–µ–Љ–Њ–Љ –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є –Њ–±–ї–∞—Б—В—М—О –Њ–Ї—А—Г–ґ–∞—О—Й–µ–≥–Њ –µ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ (—А–Є—Б.1). –£—Б–ї–Њ–≤–љ–Њ –±—Г–і–µ–Љ –љ–∞–Ј—Л–≤–∞—В—М –і–∞–љ–љ—Г—О —З–∞—Б—В–Є—Ж—Г –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Њ–є¬ї (–Є–ї–Є –і–ї—П –Ї—А–∞—В–Ї–Њ—Б—В–Є ¬Ђ—В–Њ—З–Ї–Њ–є¬ї).
–Ф–Њ–њ—Г—Б—В–Є–Љ, —З—В–Њ –і–∞–љ–љ–∞—П —З–∞—Б—В–Є—Ж–∞ —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –±–ї—Г–ґ–і–∞–µ—В –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В—П—Е —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї (—Б–Њ–≤–Љ–µ—Й–µ–љ–љ–Њ–≥–Њ —Б –љ–∞—З–∞–ї–Њ–Љ —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В X Y Z) –њ–Њ–і –і–µ–є—Б—В–≤–Є–µ–Љ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –љ–µ —Б–≤—П–Ј–∞–љ–љ—Л—Е –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є —Б–Є–ї–Њ–≤—Л—Е —Д–∞–Ї—В–Њ—А–Њ–≤.
–Я—А–Є–Љ–µ—А–Њ–Љ —В–∞–Ї–Њ–≥–Њ –њ–Њ–≤–µ–і–µ–љ–Є—П —З–∞—Б—В–Є—Ж—Л –Љ–Њ–ґ–µ—В –њ–Њ—Б–ї—Г–ґ–Є—В—М, –љ–∞–њ—А–Є–Љ–µ—А, —Е–∞–Њ—В–Є—З–µ—Б–Ї–Њ–µ –і—А–Њ–ґ–∞–љ–Є–µ —П–і—А–∞ –≤–љ—Г—В—А–Є –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є –Ї–ї–µ—В–Ї–Є.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ –њ—А–Є –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–Є —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї –Њ—В ¬Ђ—Ж–µ–љ—В—А–∞¬ї –≤–Њ–Ј–љ–Є–Ї–∞–µ—В —Б–Є–ї–∞, —Б—В—А–µ–Љ—П—Й–∞—П—Б—П –≤–µ—А–љ—Г—В—М –µ–µ –≤ –Є—Б—Е–Њ–і–љ—Л–є ¬Ђ—Ж–µ–љ—В—А¬ї. –Я—А–Є —Н—В–Њ–Љ, —З–µ–Љ –і–∞–ї—М—И–µ ¬Ђ—В–Њ—З–Ї–∞¬ї –Њ—В–Ї–ї–Њ–љ—П–µ—В—Б—П –Њ—В ¬Ђ—Ж–µ–љ—В—А–∞¬ї, —В–µ–Љ –±–Њ–ї—М—И–µ –≤–ї–Є—П–љ–Є–µ –≤–Њ–Ј–≤—А–∞—Й–∞—О—Й–µ–є —Б–Є–ї—Л.
–Т —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є –Љ–Њ–і–µ–ї–Є ¬Ђ—В–Њ—З–Ї–∞¬ї –і–Њ—Б—В–Є–≥–∞–µ—В –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–≥–Њ —Г–і–∞–ї–µ–љ–Є—П –Њ—В ¬Ђ—Ж–µ–љ—В—А–∞¬ї –Ј–∞ —Б—З–µ—В —А–∞—Б—Е–Њ–і–∞ –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Њ–є —Н–љ–µ—А–≥–Є–Є T (x,y,z,t) (—В.–µ. —Б –Ј–∞–Љ–µ–і–ї–µ–љ–Є–µ–Љ), –∞ –Ј–∞—В–µ–Љ –њ–Њ–і –і–µ–є—Б—В–≤–Є–µ–Љ –≤–Њ–Ј–≤—А–∞—Й–∞—О—Й–µ–є —Б–Є–ї—Л [–Є–ї–Є –љ–∞–Ї–Њ–њ–ї–µ–љ–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Н–љ–µ—А–≥–Є–Є U (x,y,z,t)] –Њ–љ–∞ –≤–Њ–Ј–≤—А–∞—Й–∞–µ—В—Б—П –Ї ¬Ђ—Ж–µ–љ—В—А—Г¬ї —Б —Г—Б–Ї–Њ—А–µ–љ–Є–µ–Љ. –Ч–∞ —Б—З–µ—В –њ—А–Є–Њ–±—А–µ—В–µ–љ–љ–Њ–є –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Њ–є —Н–љ–µ—А–≥–Є–Є ¬Ђ—В–Њ—З–Ї–∞¬ї –њ—А–Њ—Б–Ї–∞–Ї–Є–≤–∞–µ—В ¬Ђ—Ж–µ–љ—В—А¬ї, –Є –≤–љ–Њ–≤—М —Г–і–∞–ї—П–µ—В—Б—П –Њ—В –љ–µ–≥–Њ —Б –Ј–∞–Љ–µ–і–ї–µ–љ–Є–µ–Љ. –Ґ–∞–Ї–Њ–µ —Е–∞–Њ—В–Є—З–µ—Б–Ї–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ ¬Ђ—В–Њ—З–Ї–Є¬ї, –≤ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є –Љ–Њ–і–µ–ї–Є, –њ—А–Њ–і–Њ–ї–ґ–∞–µ—В—Б—П ¬Ђ–≤–µ—З–љ–Њ¬ї, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –µ–µ –њ–Њ–ї–љ–∞—П –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П E –≤—Б–µ–≥–і–∞ –Њ—Б—В–∞–µ—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є
–Х = T (x,y,z,t) + U (x,y,z,t) = const, (7)
–≥–і–µ T (x,y,z,t) вАУ –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Њ–є —Н–љ–µ—А–≥–Є—П ¬Ђ—В–Њ—З–Ї–Є¬ї, –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ–љ–∞—П —Б–Ї–Њ—А–Њ—Б—В—М—О –µ–µ –і–≤–Є–ґ–µ–љ–Є—П;
U (x,y,z,t) вАУ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П ¬Ђ—В–Њ—З–Ї–Є¬ї, –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ–љ–∞—П —Б–Є–ї–Њ–є (–љ–∞–њ—А–Є–Љ–µ—А, —Б–Є–ї–Њ–є —Г–њ—А—Г–≥–Њ—Б—В–Є –Њ–Ї—А—Г–ґ–∞—О—Й–µ–є —Б—А–µ–і—Л), —Б—В—А–µ–Љ—П—Й–µ–є—Б—П –≤–µ—А–љ—Г—В—М ¬Ђ—В–Њ—З–Ї—Г¬ї –≤ ¬Ђ—Ж–µ–љ—В—А¬ї —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–≥–Њ –ї–Њ–Ї–∞–ї—М–љ–Њ–≥–Њ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П (–Є–ї–Є –Ј–∞–Љ–Ї–љ—Г—В–Њ–є –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л).
–Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є –≤ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є –Љ–Њ–і–µ–ї–Є –Ї–∞–ґ–і–∞—П –Є–Ј —Н–љ–µ—А–≥–Є–є T (x,y,z,t) –Є U (x,y,z,t) ¬Ђ—В–Њ—З–Ї–Є¬ї —П–≤–ї—П–µ—В—Б—П —Б–ї—Г—З–∞–є–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є –≤—А–µ–Љ–µ–љ–Є –Є –Љ–µ—Б—В–∞ –µ–µ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї. –Э–Њ —Н—В–Є —Н–љ–µ—А–≥–Є–Є –њ–ї–∞–≤–љ–Њ –њ–µ—А–µ—В–µ–Ї–∞—О—В –і—А—Г–≥ –≤ –і—А—Г–≥–∞ —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ –Є—Е —Б—Г–Љ–Љ–∞ (—В. –µ. –њ–Њ–ї–љ–∞—П –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П –Х) –≤—Б–µ–≥–і–∞ –Њ—Б—В–∞–µ—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є.
–Х—Б–ї–Є —Б–Ї–Њ—А–Њ—Б—В—М —Е–∞–Њ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –і–≤–Є–ґ–µ–љ–Є—П ¬Ђ—В–Њ—З–Ї–Є¬ї –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї –і–∞–љ–љ–Њ–є –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л (—А–Є—Б. 1) –љ–µ–≤–µ–ї–Є–Ї–∞, —В–Њ —Б–Њ–≥–ї–∞—Б–љ–Њ –љ–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ, –Њ–љ–∞ –Њ–±–ї–∞–і–∞–µ—В –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Њ–є —Н–љ–µ—А–≥–Є–µ–є
.
(8)
–Ф–ї—П —Б–Њ–Ї—А–∞—Й–µ–љ–Є—П –Ј–∞–њ–Є—Б–µ–є –≤–Љ–µ—Б—В–Њ (8) –±—Г–і–µ–Љ –њ–Є—Б–∞—В—М
,
(9)
–≥–і–µ p—Е(t), p—Г(t), pz(t) вАУ –Љ–≥–љ–Њ–≤–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В –Є–Љ–њ—Г–ї—М—Б–∞ –±–ї—Г–ґ–і–∞—О—Й–µ–є ¬Ђ—В–Њ—З–Ї–Є¬ї,
,
(10)
.
–Т–Є–і –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Н–љ–µ—А–≥–Є–Є ¬Ђ—В–Њ—З–Ї–Є¬ї U (x,y,z,t) –љ–µ –Ї–Њ–љ–Ї—А–µ—В–Є–Ј–Є—А—Г–µ—В—Б—П.
–Ф–µ–є—Б—В–≤–Є–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї S –≤ –љ–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ [1]
(11)
–Ф–ї—П —Г–њ—А–Њ—Й–µ–љ–Є—П –≤—Л–Ї–ї–∞–і–Њ–Ї –Ј–і–µ—Б—М —А–∞—Б—Б–Љ–Њ—В—А–µ–љ –Њ–і–љ–Њ–Љ–µ—А–љ—Л–є —Б–ї—Г—З–∞–є, –љ–µ –Њ–≥—А–∞–љ–Є—З–Є–≤–∞—О—Й–Є–є –Њ–±—Й–љ–Њ—Б—В—М –Ј–∞–Ї–ї—О—З–µ–љ–Є–є. –Т —Б–ї—Г—З–∞–µ —В—А–µ—Е –Є–Ј–Љ–µ—А–µ–љ–Є–є —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П —В–Њ–ї—М–Ї–Њ —З–Є—Б–ї–Њ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–є.
–Ш–Ј-–Ј–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В–Є –і–≤–Є–ґ–µ–љ–Є—П –±–ї—Г–ґ–і–∞—О—Й–µ–є ¬Ђ—В–Њ—З–Ї–Є¬ї –љ–∞—Б –±—Г–і–µ—В –Є–љ—В–µ—А–µ—Б–Њ–≤–∞—В—М –љ–µ —Б–∞–Љ–Њ –і–µ–є—Б—В–≤–Є–µ (11), –∞ –µ–≥–Њ —Г—Б—А–µ–і–љ–µ–љ–Є–µ –њ–Њ –≤—А–µ–Љ–µ–љ–Є (–Є–ї–Є –њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є—П–Љ)
(12)
–Э–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ –і–ї—П —Н—А–≥–Њ–і–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ –Љ–µ–ґ–і—Г —Г—Б—А–µ–і–љ–µ–љ–Є–µ–Љ –њ–Њ –≤—А–µ–Љ–µ–љ–Є –Є —Г—Б—А–µ–і–љ–µ–љ–Є–µ–Љ –њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є—П–Љ.
–Ч–љ–∞–Ї –њ–ї—О—Б –≤ –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є
(12) –њ–Њ—Б—В–∞–≤–ї–µ–љ –њ–Њ—В–Њ–Љ—Г, —З—В–Њ —Г—Б—А–µ–і–љ–µ–љ–љ–∞—П
–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П
–Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞, —В. –Ї. –≤—Б–µ–≥–і–∞ —Б—В—А–µ–Љ–Є—В—Б—П
–≤–µ—А–љ—Г—В—М ¬Ђ—В–Њ—З–Ї—Г¬ї –≤ ¬Ђ—Ж–µ–љ—В—А¬ї –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ
–≤ —Б—А–µ–і–љ–µ–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–≥–Њ
–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П. –£—Б—А–µ–і–љ–µ–љ–Є–µ (12) –Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П
–њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є—П–Љ, –≤–Ј—П—В—Л–Љ –Ј–∞ –Њ–і–Є–љ –Є —В–Њ—В –ґ–µ
–њ—А–Њ–Љ–µ–ґ—Г—В–Њ–Ї –≤—А–µ–Љ–µ–љ–Є пБД
t = t2
вАУ t1.
–£—Б—А–µ–і–љ–µ–љ–љ—Г—О –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї—Г—О —Н–љ–µ—А–≥–Є—О –±–ї—Г–ґ–і–∞—О—Й–µ–є ¬Ђ—В–Њ—З–Ї–Є¬ї –њ—А–µ–і—Б—В–∞–≤–Є–Љ –≤ –≤–Є–і–µ
,
(13)
–≥–і–µ ѕБ(px) вАУ –њ–ї–Њ—В–љ–Њ—Б—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (–Я–†–Т) —Б–Њ—Б—В–∞–≤–ї—П—О—Й–µ–є –Є–Љ–њ—Г–ї—М—Б–∞ —А—Е –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї.
–£—Б—А–µ–і–љ–µ–љ–љ—Г—О –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Г—О —Н–љ–µ—А–≥–Є—О ¬Ђ—В–Њ—З–Ї–Є¬ї –њ—А–µ–і—Б—В–∞–≤–Є–Љ –≤ –≤–Є–і–µ
,
(14)
–≥–і–µ ѕБ(—Е) вАУ –Я–†–Т –Љ–µ—Б—В–∞ –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –њ—А–Њ–µ–Ї—Ж–Є–Є –љ–∞ –Њ—Б—М —Е ¬Ђ—В–Њ—З–Ї–Є¬ї, –±–ї—Г–ґ–і–∞—О—Й–µ–є –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї (—А–Є—Б.1).
–Я–Њ–і—Б—В–∞–≤–ї—П—П (13) –Є (14) –≤ —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–µ –і–µ–є—Б—В–≤–Є–µ (12), –њ–Њ–ї—Г—З–Є–Љ
(15)
–Ф–ї—П –і–∞–ї—М–љ–µ–є—И–µ–≥–Њ –≤—Л–≤–Њ–і–∞ –Њ–±–Њ—Й–µ–љ–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –љ–Є–ґ–µ –њ—А–Є–≤–µ–і–µ–љ—Л –і–≤–∞ –≤—Б–њ–Њ–Љ–Њ–≥–∞—В–µ–ї—М–љ—Л—Е –њ—Г–љ–Ї—В–∞. –Я–µ—А–≤—Л–є –њ—Г–љ–Ї—В, —П–≤–ї—П—О—Й–Є–є—Б—П —А–∞–Ј—А–∞–±–Њ—В–Ї–Њ–є –∞–≤—В–Њ—А–∞ [2, 3], –њ–Њ—Б–≤—П—Й–µ–љ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є n-–≥–Њ –њ–Њ—А—П–і–Ї–∞ n —А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –Т—В–Њ—А–Њ–є –њ—Г–љ–Ї—В ¬Ђ–Ъ–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –Є–Љ–њ—Г–ї—М—Б–∞ —З–∞—Б—В–Є—Ж—Л¬ї –≤ –Њ—Б–љ–Њ–≤–љ–Њ–Љ –њ–Њ–Ј–∞–Є–Љ—Б—В–≤–Њ–≤–∞–љ –Є–Ј —А–∞–±–Њ—В –Ф.–Ш. –С–ї–Њ—Е–Є–љ—Ж–µ–≤–∞ [5] –і–ї—П —Г–і–Њ–±—Б—В–≤–∞ —Б—Б—Л–ї–Њ–Ї.
3.
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П
–≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є n-–≥–Њ
–њ–Њ—А—П–і–Ї–∞
n
—А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ,
—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Б–њ–Њ—Б–Њ–±–∞ –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (–Я–†–Т) –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –≤ —Г–Ј–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –њ—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–є –Я–†–Т —Б–∞–Љ–Њ–≥–Њ —Н—В–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —П–≤–ї—П–µ—В—Б—П –Ї–ї—О—З–Њ–Љ –Ї –њ–Њ–љ–Є–Љ–∞–љ–Є—О –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Є –≥—А–∞–љ–Є—Ж –µ–µ –њ—А–Є–Љ–µ–љ–µ–љ–Є—П. –†–µ—И–µ–љ–Є–µ –і–∞–љ–љ–Њ–є –Ј–∞–і–∞—З–Є –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Њ–±–Њ—Б–љ–Њ–≤–∞—В—М –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї—Г—О –њ—А–Њ—Ж–µ–і—Г—А—Г –њ–µ—А–µ—Е–Њ–і–∞ –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Ї –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –Є, –љ–∞–Њ–±–Њ—А–Њ—В. –≠—В–Њ —Б—В–∞–љ–Њ–≤–Є—В—Б—П –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–Љ –≤ —Б–Є–ї—Г —В–Њ–≥–Њ, —З—В–Њ –Є–Љ–њ—Г–ї—М—Б —З–∞—Б—В–Є—Ж—Л (–Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї) –ї–Є–љ–µ–є–љ–Њ —Б–≤—П–Ј–∞–љ —Б –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –Њ—В –µ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л px= m¬ЈпВґx/пВґt = mx„≥. –Ш–Љ–µ–љ–љ–Њ —Н—В–Њ –Њ–±—Б—В–Њ—П—В–µ–ї—М—Б—В–≤–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Њ–±–Њ—Б–љ–Њ–≤–∞—В—М —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г –Є–Љ–њ—Г–ї—М—Б–љ—Л–Љ –Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П–Љ–Є –Ї–≤–∞–љ—В–Њ–≤–Њ - –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –Є—Б—Е–Њ–і—П –љ–µ –Є–Ј —Д–µ–љ–Њ–Љ–µ–љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е –њ—А–Є–љ—Ж–Є–њ–Њ–≤ –Ї–Њ—А–њ—Г—Б–Ї—Г–ї—П—А–љ–Њ-–≤–Њ–ї–љ–Њ–≤–Њ–≥–Њ –і—Г–∞–ї–Є–Ј–Љ–∞ –Ы—Г–Є –і–µ –С—А–Њ–є–ї—П, –∞ –Є–Ј –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј–Є –Љ–µ–ґ–і—Г –Я–†–Т —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –Є –Я–†–Т –µ–≥–Њ –њ–µ—А–≤–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –њ—А–Њ–±–ї–µ–Љ–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –Я–†–Т ѕБ1[ќЊn(t)] - –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є n-–≥–Њ –њ–Њ—А—П–і–Ї–∞ n —А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ (t), –њ—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–є —В–Њ–ї—М–Ї–Њ –µ–≥–Њ –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –Я–†–Т ѕБ1[ќЊ (t)], –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –≤ —А—П–і–µ –і—А—Г–≥–Є—Е –Ј–∞–і–∞—З —А–∞–і–Є–Њ—Д–Є–Ј–Є–Ї–Є –Є —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є.
–Ю—В–Љ–µ—В–Є–Љ –≤–љ–∞—З–∞–ї–µ –Њ–±—Й–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ –њ–µ—А–≤–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(t). –Ф–ї—П —Н—В–Њ–≥–Њ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Љ –µ–≥–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є (—А–Є—Б. 2).
–Ш–Ј —А–Є—Б. 2 –≤–Є–і–љ–Њ, —З—В–Њ –Ј–љ–∞—З–µ–љ–Є–µ —Б–ї—Г—З–∞–є–љ–Њ–є
–≤–µ–ї–Є—З–Є–љ—Л ќЊ(ti)
–≤ —Б–µ—З–µ–љ–Є–Є ti
–Є –Ј–љ–∞—З–µ–љ–Є–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Н—В–Њ–≥–Њ
–њ—А–Њ—Ж–µ—Б—Б–∞
–њ—А–Є —В–Њ–Љ –ґ–µ –Ј–љ–∞—З–µ–љ–Є–Є –∞—А–≥—Г–Љ–µ–љ—В–∞ ti
—П–≤–ї—П—О—В—Б—П –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л–Љ–Є, –∞
—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є –љ–µ–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є,
—Б–ї—Г—З–∞–є–љ—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є. –Ф–∞–љ–љ–Њ–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ
–Љ–Њ–ґ–µ—В –±—Л—В—М –≤—Л—А–∞–ґ–µ–љ–Њ –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Є [6]
(16)
–†–Є—Б. 2. –†–µ–∞–ї–Є–Ј–∞—Ж–Є–Є, –њ–Њ –Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ, –Њ–і–Є–љ —А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ
—Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(t)
–і–µ пАЉ пАЊ –Њ–Ј–љ–∞—З–∞–µ—В —Г—Б—А–µ–і–љ–µ–љ–Є–µ –њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є—П–Љ. –Ч–і–µ—Б—М —Г—З—В–µ–љ–Њ, —З—В–Њ –Њ–њ–µ—А–∞—Ж–Є–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є—П –Є —Г—Б—А–µ–і–љ–µ–љ–Є—П –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ —П–≤–ї—П—О—В—Б—П –Ї–Њ–Љ–Љ—Г—В–∞—В–Є–≤–љ—Л–Љ–Є –Њ–њ–µ—А–∞—Ж–Є—П–Љ–Є, –Є —З—В–Њ –≤—Б–µ —Г—Б—А–µ–і–љ–µ–љ–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –≤ —Г–Ј–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ –њ—А–Њ—Ж–µ—Б—Б–∞ —П–≤–ї—П—О—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –µ–≥–Њ –і–Є—Б–њ–µ—А—Б–Є—П –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –≤—А–µ–Љ–µ–љ–Є
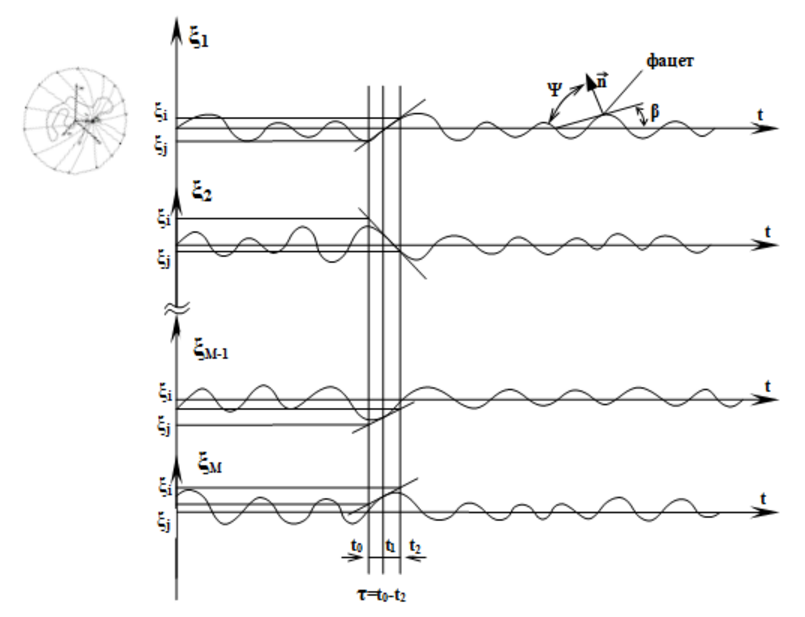
–†–µ–∞–ї–Є–Ј–∞—Ж–Є–Є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(ti), –њ–Њ–Ї–∞–Ј–∞–љ–љ—Л–µ –љ–∞ (—А–Є—Б. 2), –Љ–Њ–≥—Г—В –Є–љ—В–µ—А–њ—А–µ—В–Є—А–Њ–≤–∞—В—М—Б—П, –Ї–∞–Ї —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є –њ—А–Њ–µ–Ї—Ж–Є–Є –љ–∞ –Њ—Б—М —Е –Љ–µ—Б—В–∞ –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –±–ї—Г–ґ–і–∞—О—Й–µ–є –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї —Е (t) = ќЊ (ti) (—Б–Љ. —А–Є—Б.1).
–°—Г—Й–µ—Б—В–≤—Г–µ—В —В–∞–Ї–ґ–µ –Ї–ї–∞—Б—Б —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤, –≤ –Ї–Њ—В–Њ—А—Л—Е ќЊ(ti) = ќЊi –Є ќЊпВҐ (ti) = ќЊiпВҐ —П–≤–ї—П—О—В—Б—П –љ–µ —В–Њ–ї—М–Ї–Њ –љ–µ–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є, –љ–Њ –Є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л–Љ–Є —Б–ї—Г—З–∞–є–љ—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є. –Ъ –љ–Є–Љ –Њ—В–љ–Њ—Б–Є—В—Б—П —Б–ї—Г—З–∞–є–љ—Л–є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–є –≥–∞—Г—Б—Б–Њ–≤—Б–Ї–Є–є –њ—А–Њ—Ж–µ—Б—Б [6,7].
–Ю–і–љ–∞–Ї–Њ –і–∞–ґ–µ –њ—А–Є —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —Б–ї—Г—З–∞–є–љ—Л—Е –≤–µ–ї–Є—З–Є–љ ќЊi –Є ќЊпВҐi –љ–µ–Ї–∞—П —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г –Я–†–Т ѕБ1(ќЊi) –Є –Я–†–Т ѕБ1(ќЊiпВҐ ) —Б—Г—Й–µ—Б—В–≤—Г–µ—В. –≠—В–Њ –≤—Л—В–µ–Ї–∞–µ—В –Є–Ј –Є–Ј–≤–µ—Б—В–љ–Њ–є –њ—А–Њ—Ж–µ–і—Г—А—Л (—Б–Љ. [6,7]) –њ–Њ–ї—Г—З–µ–љ–Є—П –Я–†–Т –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є ѕБ1(ќЊпВҐi) –њ—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–є –і–≤—Г—Е–Љ–µ—А–љ–Њ–є –Я–†–Т —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞
.
(17)
–Ф–ї—П —Н—В–Њ–≥–Њ –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є (17) –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–і–µ–ї–∞—В—М –Ј–∞–Љ–µ–љ—Г –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е
, (18)
–≥–і–µ
—Б —П–Ї–Њ–±–Є–∞–љ–Њ–Љ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П [J] = ѕД. –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –Є–Ј –Я–†–Т (17) –њ–Њ–ї—Г—З–Є–Љ
.
(19)
–Ф–∞–ї–µ–µ, –Є–љ—В–µ–≥—А–Є—А—Г—П –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –њ–Њ ќЊk, –љ–∞–є–і–µ–Љ –Є—Б–Ї–Њ–Љ—Г—О –Я–†–Т –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –Є—Б—Е–Њ–і–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –≤ —Б–µ—З–µ–љ–Є–Є tk [6,7]:
.
(20)
–§–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ—Ж–µ–і—Г—А–∞ (17) вАУ (20) –њ–Њ–Ј–≤–Њ–ї—П–µ—В —А–µ—И–Є—В—М –Ј–∞–і–∞—З—Г –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Я–†–Т ѕБ1(ќЊпВҐ ) –њ—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–є –і–≤—Г—Е–Љ–µ—А–љ–Њ–є –Я–†–Т (17). –Ю–і–љ–∞–Ї–Њ –і–≤—Г—Е–Љ–µ—А–љ—Л–µ –Я–†–Т –Њ–њ—А–µ–і–µ–ї–µ–љ—Л –і–ї—П –Њ—З–µ–љ—М –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–≥–Њ –Ї–ї–∞—Б—Б–∞ —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤. –Я–Њ—Н—В–Њ–Љ—Г –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –њ–Њ–ї—Г—З–µ–љ–Є—П –Я–†–Т ѕБ1(ќЊiпВҐ ) –њ—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–є –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –Я–†–Т ѕБ1(ќЊi).
–Ф–ї—П —А–µ—И–µ–љ–Є—П –њ–Њ—Б—В–∞–≤–ї–µ–љ–љ–Њ–є –Ј–∞–і–∞—З–Є –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ–Є —Б–≤–Њ–є—Б—В–≤–∞–Љ–Є —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤:
1. –Ф–≤—Г—Е–Љ–µ—А–љ–∞—П –Я–†–Т –ї—О–±–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–∞ –≤ –≤–Є–і–µ [6,7]–†–µ–∞–ї–Є–Ј–∞—Ж–Є–Є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞
(21)
–≥–і–µ ѕБ(ќЊj, tj /ќЊi, ti) вАУ —Г—Б–ї–Њ–≤–љ–∞—П –Я–†–Т.
2. –Ф–ї—П —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –≤ —Г–Ј–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —В–Њ–ґ–і–µ—Б—В–≤–Њ [6,7]
.
(22)
3. –£—Б–ї–Њ–≤–љ–∞—П –Я–†–Т —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –њ—А–Є ti вЖТ tj –≤—Л—А–Њ–ґ–і–∞–µ—В—Б—П –≤ –і–µ–ї—М—В–∞-—Д—Г–љ–Ї—Ж–Є—О [7]
.
(23)
–Э–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –≤—Л—И–µ–њ–µ—А–µ—З–Є—Б–ї–µ–љ–љ—Л—Е —Б–≤–Њ–є—Б—В–≤ –њ–Њ–њ—Л—В–∞–µ–Љ—Б—П —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М —Б–ї—Г—З–∞–є–љ—Л–є –њ—А–Њ—Ж–µ—Б—Б –љ–∞ —Г—З–∞—Б—В–Ї–µ ] ti вАУ ѕД0; ti + ѕД [ –њ—А–Є ѕДвЖТ0 –њ–Њ—Б—А–µ–і—Б—В–≤–Њ–Љ —Б–ї–µ–і—Г—О—Й–µ–є —Д–Њ—А–Љ–∞–ї—М–љ–Њ–є –њ—А–Њ—Ж–µ–і—Г—А—Л. –Я–†–Т ѕБ1(ќЊi) = ѕБ1(ќЊi, ti) –Є ѕБ1(ќЊj) = ѕБ1(ќЊj, tj) –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –і–≤—Г—Е —Д—Г–љ–Ї—Ж–Є–є
(24)
–≥–і–µ ѕЖ(ќЊi) вАУ –њ–ї–Њ—В–љ–Њ—Б—В—М –∞–Љ–њ–ї–Є—В—Г–і—Л –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (–Я–Р–Т) —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л ќЊi –≤ —Б–µ—З–µ–љ–Є–Є ti.
–Ф–ї—П —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —В–Њ–ґ–і–µ—Б—В–≤–Њ
(25)
–≤ —З–µ–Љ –ї–µ–≥–Ї–Њ —Г–±–µ–і–Є—В—М—Б—П, –≤–Ј—П–≤ –Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–Њ—А–µ–љ—М –Њ—В –Њ–±–µ–Є—Е —З–∞—Б—В–µ–є —В–Њ–ґ–і–µ—Б—В–≤–∞ (22). –Ґ–Њ–≥–і–∞, —Б–Њ–≥–ї–∞—Б–љ–Њ (24), –њ–Њ–ї—Г—З–Є–Љ (25). –Ю—В–Љ–µ—В–Є–Љ, —З—В–Њ —В–Њ–ґ–і–µ—Б—В–≤–Њ (25) –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ –Є –і–ї—П –±–Њ–ї—М—И–Є–љ—Б—В–≤–∞ –љ–µ—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л—Е —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –њ—А–Є ѕДвЖТ0, —В. –µ.
.
(26)
–Я—А–Є –≤—Л–њ–Њ–ї–љ–µ–љ–Є–Є —Г—Б–ї–Њ–≤–Є—П (25) –≤—Л—А–∞–ґ–µ–љ–Є–µ (21) –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Њ –≤ —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–Љ –≤–Є–і–µ
(27)
–≥–і–µ ѕБ(ќЊj /ќЊi) вАУ —Г—Б–ї–Њ–≤–љ–∞—П –Я–†–Т, –Є–ї–Є –≤ —А–∞–Ј–≤–µ—А–љ—Г—В–Њ–Љ –≤–Є–і–µ
(28)
–£—Б—В—А–µ–Љ–Є–Љ –≤ (28) ѕД –Ї –љ—Г–ї—О, –љ–Њ —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ–±—Л –Є–љ—В–µ—А–≤–∞–ї ѕД —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —Б–ї–µ–≤–∞ –Є —Б–њ—А–∞–≤–∞ —Б—В—П–≥–Є–≤–∞–ї—Б—П –≤ —В–Њ—З–Ї—Г tk = (tj вАУ ti)/2. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–µ —Б—В—П–≥–Є–≤–∞–љ–Є–µ ѕД –Ї –љ—Г–ї—О —З–µ—А–µ–Ј ѕДвЖТ ¬± 0, —В–Њ–≥–і–∞ —Б —Г—З–µ—В–Њ–Љ (23) –Є–Ј (27) –њ–Њ–ї—Г—З–Є–Љ
(29)
–≥–і–µ ќЊik вАУ —А–µ–Ј—Г–ї—М—В–∞—В —Б—В—А–µ–Љ–ї–µ–љ–Є—П —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л ќЊ(ti) –Ї —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–µ ќЊ(tk) —Б–ї–µ–≤–∞ (—В. –µ. ќЊi вЖТќЊkвАУ= ќЊik вАУ –њ—А–µ–і–µ–ї —Б–ї–µ–≤–∞ –њ—А–Є ti вЖТ tkвАУ);
ќЊjk вАУ —А–µ–Ј—Г–ї—М—В–∞—В —Б—В—А–µ–Љ–ї–µ–љ–Є—П —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л ќЊ(tj) –Ї —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–µ ќЊ(tk) —Б–њ—А–∞–≤–∞ (—В. –µ. ќЊj вЖТ ќЊk+= ќЊjk вАУ –њ—А–µ–і–µ–ї —Б–њ—А–∞–≤–∞ –њ—А–Є tj вЖТ tk+).
–Я—А–Њ–Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–≤ –Њ–±–µ —З–∞—Б—В–Є –≤—Л—А–∞–ґ–µ–љ–Є—П (29) –њ–Њ ќЊik –Є ќЊjk, –њ–Њ–ї—Г—З–Є–Љ —В–Њ–ґ–і–µ—Б—В–≤–Њ
.
(30)
–Т—Л—А–∞–ґ–µ–љ–Є–µ (30) —П–≤–ї—П–µ—В—Б—П —Д–Њ—А–Љ–∞–ї—М–љ—Л–Љ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ —В–Њ–ґ–і–µ—Б—В–≤–Њ–Љ –Є–Ј —В–µ–Њ—А–Є–Є –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є, —Г—З–Є—В—Л–≤–∞—О—Й–Є–Љ —Б–≤–Њ–є—Б—В–≤–∞ –і–µ–ї—М—В–∞-—Д—Г–љ–Ї—Ж–Є–Є (ќі-—Д—Г–љ–Ї—Ж–Є–Є). –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –љ–∞–њ–Њ–ї–љ–Є—В—М —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ —Б–Њ–і–µ—А–ґ–∞–љ–Є–µ–Љ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–∞–і–∞—В—М –Ї–Њ–љ–Ї—А–µ—В–љ—Л–є –≤–Є–і –і–∞–љ–љ–Њ–є ќі-—Д—Г–љ–Ї—Ж–Є–Є.
–Ю–њ—А–µ–і–µ–ї–Є–Љ –≤–Є–і ќі-—Д—Г–љ–Ї—Ж–Є–Є –і–ї—П –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞.
–•–Њ—В—П –Љ–∞—А–Ї–Њ–≤—Б–Ї–Є–µ —Б–ї—Г—З–∞–є–љ—Л–µ –њ—А–Њ—Ж–µ—Б—Б—Л (—В. –µ. –њ—А–Њ—Ж–µ—Б—Б—Л –±–µ–Ј –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ–Њ–≥–Њ –њ–Њ—Б–ї–µ–і—Б—В–≤–Є—П) –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В —Б–Њ–±–Њ–є —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л–є –Ї–ї–∞—Б—Б —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤, –Ј–љ–∞—З–µ–љ–Є–µ –Є—Е –Њ—З–µ–љ—М –≤–µ–ї–Є–Ї–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤—Л–і–µ–ї—П—О—Й–Є–µ –Є—Е —Г—Б–ї–Њ–≤–Є—П –Њ–Ї–∞–Ј—Л–≤–∞—О—В—Б—П –≤—Л–њ–Њ–ї–љ–µ–љ–љ—Л–Љ–Є –≤ —И–Є—А–Њ–Ї–Њ–є –Њ–±–ї–∞—Б—В–Є –њ—А–Є–ї–Њ–ґ–µ–љ–Є–є —В–µ–Њ—А–Є–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є [7].
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –љ–µ–њ—А–µ—А—Л–≤–љ—Л–є –Љ–∞—А–Ї–Њ–≤—Б–Ї–Є–є –њ—А–Њ—Ж–µ—Б—Б, –і–ї—П –Ї–Њ—В–Њ—А–Њ–≥–Њ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –≠–є–љ—И—В–µ–є–љ–∞ - –§–Њ–Ї–Ї–µ—А–∞ [7,8]
, (31)
–≥–і–µ –Т вАУ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –і–Є—Д—Д—Г–Ј–Є–Є.
–≠—В–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —В–Є–њ–∞ –Є–Љ–µ–µ—В —В—А–Є —А–µ—И–µ–љ–Є—П, –Њ–і–љ–Њ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Њ –≤ –≤–Є–і–µ [7,8]
(32)
–≥–і–µ q вАУ –Њ–±–Њ–±—Й–µ–љ–љ—Л–є –њ–∞—А–∞–Љ–µ—В—А.
–Я—А–Є tj вАУ ti = ѕД вЖТ ¬± 0 –Є–Ј (32) –њ–Њ–ї—Г—З–Є–Љ –Њ–і–љ–Њ –Є–Ј –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–є ќі-—Д—Г–љ–Ї—Ж–Є–Є
(33)
–Я–Њ–і—Б—В–∞–≤–Є–≤ –њ–Њ–ї—Г—З–µ–љ–љ—Г—О ќі-—Д—Г–љ–Ї—Ж–Є—О (33) –≤ –≤—Л—А–∞–ґ–µ–љ–Є–µ (30), –њ–Њ–ї—Г—З–Є–Љ
.
(34)
–Я–Њ–Љ–µ–љ—П–≤ –≤ (34) –њ–Њ—А—П–і–Њ–Ї –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П, –Є–Љ–µ–µ–Љ
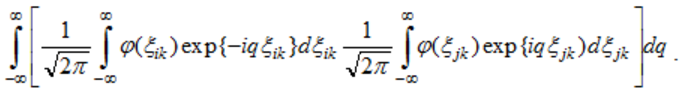 (35)
(35)
–£—З—В–µ–Љ, —З—В–Њ, —Б–Њ–≥–ї–∞—Б–љ–Њ (25), ѕЖ(ќЊik) = ѕЖ(ќЊjk) –Є —З—В–Њ —Б —Г—З–µ—В–Њ–Љ —Б–≤–Њ–є—Б—В–≤ ќі-—Д—Г–љ–Ї—Ж–Є–Є ќЊik = ќЊjk = ќЊk . –Я—А–Є —Н—В–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–µ (35) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
(36)
–≥–і–µ
(37)
(38)
–Я–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ
–≤—Л—А–∞–ґ–µ–љ–Є–µ
–≤
–Є–љ—В–µ–≥—А–∞–ї–µ (36) –Њ—В–≤–µ—З–∞–µ—В –≤—Б–µ–Љ —В—А–µ–±–Њ–≤–∞–љ–Є—П–Љ
–Я–†–Т ѕБ(q)
—Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л q:
.
(39)
–Т—Л—П—Б–љ–Є–Љ —В–µ–њ–µ—А—М, —З—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є —Б–ї—Г—З–∞–є–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ q. –Ф–ї—П —Н—В–Њ–≥–Њ –≤–µ—А–љ–µ–Љ—Б—П –Ї —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—О –≤—Л—А–∞–ґ–µ–љ–Є—П (32). –†–µ–Ј—Г–ї—М—В–∞—В –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є —Н—В–Њ–≥–Њ –≤—Л—А–∞–ґ–µ–љ–Є—П –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –≤–µ–ї–Є—З–Є–љ—Л q. –Я–Њ—Н—В–Њ–Љ—Г –µ–µ –Љ–Њ–ґ–љ–Њ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М –Ї–∞–Ї –љ–µ–Ї—Г—О –Њ–±–Њ–±—Й–µ–љ–љ—Г—О —З–∞—Б—В–Њ—В—Г. –Ю–і–љ–∞–Ї–Њ —Д–Є–Ј–Є—З–µ—Б–Ї–∞—П –њ–Њ—Б—В–∞–љ–Њ–≤–Ї–∞ –Ј–∞–і–∞—З–Є –Є —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є –Ј–∞–њ–Є—Б–Є –≤—Л—А–∞–ґ–µ–љ–Є—П (32) –љ–∞–Ї–ї–∞–і—Л–≤–∞—О—В –љ–∞ –≤–µ–ї–Є—З–Є–љ—Г q —Б–ї–µ–і—Г—О—Й–Є–µ –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П:
1) –≤–µ–ї–Є—З–Є–љ–∞ q –і–Њ–ї–ґ–љ–∞ —Е–∞—А–∞–Ї—В–µ—А–Є–Ј–Њ–≤–∞—В—М —Б–ї—Г—З–∞–є–љ—Л–є –њ—А–Њ—Ж–µ—Б—Б –≤ –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ ]ti вАУ ѕД0; ti+ ѕД[ –њ—А–Є ѕДвЖТ 0;
2) –≤–µ–ї–Є—З–Є–љ–∞ q, —Б–Њ–≥–ї–∞—Б–љ–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є –Ј–∞–њ–Є—Б–Є –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –≤—Л—А–∞–ґ–µ–љ–Є—П (32), –і–Њ–ї–ґ–љ–∞ –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—В—М –Љ–љ–Њ–ґ–µ—Б—В–≤—Г –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ—Л—Е —З–Є—Б–µ–ї (q пГО RпВҐ), –Є–Љ–µ—О—Й–µ–Љ—Г –Љ–Њ—Й–љ–Њ—Б—В—М –Ї–Њ–љ—В–Є–љ—Г—Г–Љ–∞, —В. –µ. q –і–Њ–ї–ґ–љ–∞ –Є–Љ–µ—В—М –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –њ—А–Є–љ–Є–Љ–∞—В—М –ї—О–±–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Є–Ј –і–Є–∞–њ–∞–Ј–Њ–љ–∞ ]вАУ вИЮ, вИЮ [;
3) q –і–Њ–ї–ґ–љ–∞ –±—Л—В—М —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–Њ–є.
–Т—Б–µ–Љ —В—А–µ–Љ —В—А–µ–±–Њ–≤–∞–љ–Є—П–Љ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В –ї—О–±–∞—П –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е —Б–ї—Г—З–∞–є–љ—Л—Е –≤–µ–ї–Є—З–Є–љ, —Б–≤—П–Ј–∞–љ–љ—Л—Е —Б–Њ —Б–ї—Г—З–∞–є–љ—Л–Љ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ –љ–∞ –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ ѕД:
(40)
–Ю–і–љ–∞–Ї–Њ —Н—В–Є —Б–ї—Г—З–∞–є–љ—Л–µ –≤–µ–ї–Є—З–Є–љ—Л —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—В –њ—А–Њ—Ж–µ—Б—Б –љ–∞ –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ –≤—А–µ–Љ–µ–љ–Є ѕД –љ–µ –≤ —А–∞–≤–љ–Њ–є —Б—В–µ–њ–µ–љ–Є. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Њ–і–љ—Г –Є–Ј —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –§—Г–љ–Ї—Ж–Є—П ќЊ(t) (—А–Є—Б. 2) –≤ –Є–љ—В–µ—А–≤–∞–ї–µ [ti ; tj = ti + 2ѕД] –њ—А–Є ѕД < ѕД–Ї–Њ—А (–≥–і–µ ѕД–Ї–Њ—А вАУ —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞) –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞–Ј–ї–Њ–ґ–µ–љ–∞ –≤ —А—П–і –Ґ–µ–є–ї–Њ—А–∞-–Ь–∞–Ї–ї–Њ—А–µ–љ–∞
(41)
–Ч–∞–њ–Є—И–µ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–µ (41) –≤ —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–Љ –≤–Є–і–µ
(42)
–Ш–Ј –≤—Л—А–∞–ґ–µ–љ–Є—П (42) –≤–Є–і–љ–Њ, –≤—Б–µ —Б–ї—Г—З–∞–є–љ—Л–µ –≤–µ–ї–Є—З–Є–љ—Л (40) –Є–Љ–µ—О—В –Ј–љ–∞—З–µ–љ–Є–µ –њ—А–Є –њ–µ—А–µ—Е–Њ–і–µ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(t) –Є–Ј —В–Њ—З–Ї–Є (ќЊi, ti) –≤ —В–Њ–Ї—Г (ќЊi , tj = ti + ѕД), –љ–Њ –љ–µ –≤ —А–∞–≤–љ–Њ–є —Б—В–µ–њ–µ–љ–Є. –Ґ–∞–Ї –ґ–µ –Ї–∞–Ї –≤ (32), —Г—Б—В—А–µ–Љ–Є–Љ пБі –Ї –љ—Г–ї—О, –њ—А–Є —Н—В–Њ–Љ (42) —Б–≤–Њ–і–Є—В—Б—П –Ї —В–Њ–ґ–і–µ—Б—В–≤—Г
(43)
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –µ–і–Є–љ—Б—В–≤–µ–љ–љ–Њ–є —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–Њ–є, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–µ–є –≤—Б–µ–Љ –≤—Л—И–µ–њ–µ—А–µ—З–Є—Б–ї–µ–љ–љ—Л–Љ —В—А–µ–±–Њ–≤–∞–љ–Є—П–Љ –љ–∞ –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–Љ –≤—А–µ–Љ–µ–љ–љ–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ [ti = tk вАУ ѕД/2; tj = tk+ ѕД/2], –њ—А–Є ѕДвЖТ ¬±0, —П–≤–ї—П–µ—В—Б—П –њ–µ—А–≤–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –Є—Б—Е–Њ–і–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ'k –≤ —Б–µ—З–µ–љ–Є–Є tk . –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Њ—Б—В–∞–µ—В—Б—П –њ–Њ–ї–Њ–ґ–Є—В—М, —З—В–Њ —Б–ї—Г—З–∞–є–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ q –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є (32) –ї–Є–љ–µ–є–љ–Њ —Б–≤—П–Ј–∞–љ–∞ —В–Њ–ї—М–Ї–Њ —Б ќЊ'k , —В. –µ.
(44)
–≥–і–µ 1/ќЈ вАУ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є.
–Я–Њ–і—Б—В–∞–≤–ї—П—П (44) –≤ (36) вАУ (39), –њ–Њ–ї—Г—З–Є–Љ —Б–ї–µ–і—Г—О—Й—Г—О –Є—Б–Ї–Њ–Љ—Г—О –њ—А–Њ—Ж–µ–і—Г—А—Г –њ–Њ–ї—Г—З–µ–љ–Є—П –Я–†–Т –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є ѕБ(ќЊпВҐk) —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(t) –≤ —Б–µ—З–µ–љ–Є–Є tk –њ—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–є –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –Я–†–Т ѕБ(ќЊk) –≤ —В–Њ–Љ –ґ–µ —Б–µ—З–µ–љ–Є–Є:
1. –Ч–∞–і–∞–љ–љ–∞—П –Њ–і–љ–Њ–Љ–µ—А–љ–∞—П –Я–†–Т ѕБ(ќЊ) –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В—Б—П –≤ –≤–Є–і–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –і–≤—Г—Е –њ–ї–Њ—В–љ–Њ—Б—В–µ–є –∞–Љ–њ–ї–Є—В—Г–і –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (–Я–Р–Т) ѕЖ(ќЊ):
.
(45)
2. –Ю—Б—Г—Й–µ—Б—В–≤–ї—П—О—В—Б—П –і–≤–∞ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –§—Г—А—М–µ
,
(46)
. (47)
3. –Ю–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ –і–ї—П –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –њ–Њ–ї—Г—З–Є–Љ –Є—Б–Ї–Њ–Љ—Г—О –Я–†–Т –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є
.
(48)
–Ф–ї—П –≤—Л—П—Б–љ–µ–љ–Є—П —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Љ—Л—Б–ї–∞ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є 1/ќЈ –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Б—А–∞–≤–љ–µ–љ–Є–µ–Љ —Б –Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є. –Ф–∞–љ–љ—Л–є –њ–Њ–і—Е–Њ–і –љ–µ–±–µ–Ј—Г–њ—А–µ—З–µ–љ —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Б—В—А–Њ–≥–Њ—Б—В–Є, –љ–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Ї–Њ–љ–Ї—А–µ—В–љ—Л–є, –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤–∞–ґ–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–є –≥–∞—Г—Б—Б–Њ–≤—Б–Ї–Є–є, —Б–ї—Г—З–∞–є–љ—Л–є –њ—А–Њ—Ж–µ—Б—Б. –Я—А–Є —Н—В–Њ–Љ –≤ –Ї–∞–ґ–і–Њ–Љ —Б–µ—З–µ–љ–Є–Є —Н—В–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Б–ї—Г—З–∞–є–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ ќЊ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–∞ –њ–Њ –≥–∞—Г—Б—Б–Њ–≤–Њ–Љ—Г –Ј–∞–Ї–Њ–љ—Г:
,
(49)
–≥–і–µ пБ≥ 2ќЊ –Є –∞ќЊ вАУ –і–Є—Б–њ–µ—А—Б–Є—П –Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ –Є—Б—Е–Њ–і–љ–Њ–≥–Њ –≥–∞—Г—Б—Б–Њ–≤–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(t).
–Ю—Б—Г—Й–µ—Б—В–≤–ї—П—П —Б –Я–†–Т (49) –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –Њ–њ–µ—А–∞—Ж–Є–є (45) вАУ (48), –њ–Њ–ї—Г—З–Є–Љ –Я–†–Т –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞:
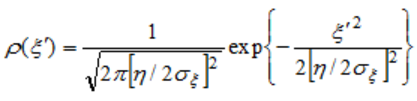 ,
(50)
,
(50)
–° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л, —Б –њ–Њ–Љ–Њ—Й—М—О –Є–Ј–≤–µ—Б—В–љ–Њ–є
–њ—А–Њ—Ж–µ–і—Г—А—Л (17) вАУ (20) –і–ї—П –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ–≥–Њ
—Б–ї—Г—З–∞—П –њ–Њ–ї—Г—З–Є–Љ [6,7]
,
(51)
–≥–і–µ ѕГќЊ' = ѕГќЊ /ѕД–Ї–Њ—А, ѕД–Ї–Њ—А вАУ —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Є—Б—Е–Њ–і–љ–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ќЊ(t).
–°—А–∞–≤–љ–Є–≤–∞—П –≤—Л—А–∞–ґ–µ–љ–Є—П (50) –Є (51), –љ–∞—Е–Њ–і–Є–Љ, —З—В–Њ –њ—А–Є
(52)
—Н—В–Є –Я–†–Т –њ–Њ–ї–љ–Њ—Б—В—М—О —Б–Њ–≤–њ–∞–і–∞—О—В.
–Т—Л—А–∞–ґ–µ–љ–Є–µ (52) –њ–Њ–ї—Г—З–µ–љ–Њ –і–ї—П –≥–∞—Г—Б—Б–Њ–≤–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞, –љ–Њ ѕГќЊ вАУ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Є ѕД –Ї–Њ—А вАУ —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є - —Н—В–Њ –Њ—Б–љ–Њ–≤–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –ї—О–±–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –Т—Б–µ –Њ—Б—В–∞–ї—М–љ—Л–µ –љ–∞—З–∞–ї—М–љ—Л–µ –Є —Ж–µ–љ—В—А–∞–ї—М–љ—Л–µ –Љ–Њ–Љ–µ–љ—В—Л –≤ —Б–ї—Г—З–∞–µ –љ–µ–≥–∞—Г—Б—Б–Њ–≤–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л ќЊ(t) –і–∞–і—Г—В –Љ–∞–ї—Л–є (–љ–µ–Ј–љ–∞—З–Є—В–µ–ї—М–љ—Л–є) –≤–Ї–ї–∞–і –≤ –≤—Л—А–∞–ґ–µ–љ–Є–µ (52), –њ–Њ—Н—В–Њ–Љ—Г —Б –≤—Л—Б–Њ–Ї–Њ–є —Б—В–µ–њ–µ–љ—М—О –і–Њ—Б—В–Њ–≤–µ—А–љ–Њ—Б—В–Є –Љ–Њ–ґ–љ–Њ —Г—В–≤–µ—А–ґ–і–∞—В—М, —З—В–Њ –Њ–љ–Њ –њ—А–Є–Љ–µ–љ–Є–Љ–Њ –і–ї—П –±–Њ–ї—М—И–Њ–≥–Њ –Ї–ї–∞—Б—Б–∞ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л—Е —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤.
–Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ—В–Љ–µ—В–Є—В—М, —З—В–Њ –≤ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–µ –Є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –і–ї—П –њ–µ—А–µ—Е–Њ–і–∞ –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є —Б–Њ—Б—В–Њ—П–љ–Є—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –Ї –µ–µ –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—О –њ—А–Є–Љ–µ–љ—П–µ—В—Б—П —Д–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ—Ж–µ–і—Г—А–∞, –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –њ–Њ–ї–љ–Њ—Б—В—М—О –∞–љ–∞–ї–Њ–≥–Є—З–љ–∞—П –њ—А–Њ—Ж–µ–і—Г—А–µ (45) вАУ (48). –†–∞–Ј–ї–Є—З–Є–µ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П —В–Њ–ї—М–Ї–Њ –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є 1/ќЈ.
–Т –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ —Е–Њ—А–Њ—И–Њ –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –µ—Б–ї–Є –њ—А–Њ–µ–Ї—Ж–Є—П –љ–∞ –Њ—Б—М —Е –њ–Њ–ї–Њ–ґ–µ–љ–Є—П —Б–≤–Њ–±–Њ–і–љ–Њ–є —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л, –љ–∞–њ—А–Є–Љ–µ—А, —Н–ї–µ–Ї—В—А–Њ–љ–∞ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П –≥–∞—Г—Б—Б–Њ–≤—Л–Љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ [9]
,
(53)
–≥–і–µ ѕГx вАУ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ (—Д–ї—Г–Ї—В—Г–∞—Ж–Є—П) –њ—А–Њ–µ–Ї—Ж–Є–Є –љ–∞ –Њ—Б—М —Е –њ–Њ–ї–Њ–ґ–µ–љ–Є—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Б—А–µ–і–љ–µ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П (—В.–µ. ¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б–Є—Б—В–µ–Љ—Л), —В–Њ –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ –Њ–њ–µ—А–∞—Ж–Є–є, –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л—Е –Њ–њ–µ—А–∞—Ж–Є—П–Љ (45) вАУ (48), –њ–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ –Я–†–Т —Б–Њ—Б—В–∞–≤–ї—П—О—Й–µ–є –Є–Љ–њ—Г–ї—М—Б–∞ —А—Е —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л —В–Њ–ґ–µ –≥–∞—Г—Б—Б–Њ–≤–∞ [9]
(54)
—Б–Њ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–љ—Л–Љ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ–Љ
,
(55)
–≥–і–µ пБ® = 1,055¬Ј10-34 –Ф–ґ/–У—Ж вАУ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞.
–Х—Б–ї–Є —В–µ–њ–µ—А—М —Г—З–µ—Б—В—М, —З—В–Њ —Б–Њ—Б—В–∞–≤–ї—П—О—Й–∞—П –Є–Љ–њ—Г–ї—М—Б–∞ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л (–љ–∞–њ—А–Є–Љ–µ—А, —Н–ї–µ–Ї—В—А–Њ–љ–∞) —А—Е —А–∞–≤–љ–∞
,
(56)
–≥–і–µ me - –Љ–∞—Б—Б–∞ –њ–Њ–Ї–Њ—П —Н–ї–µ–Ї—В—А–Њ–љ–∞, —В–Њ –Я–†–Т (54) —Б —Г—З–µ—В–Њ–Љ (55) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
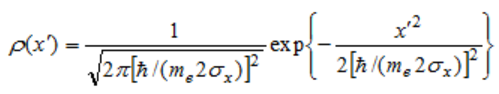 .
(57)
.
(57)
–°—А–∞–≤–љ–Є–≤–∞—П (50) –Є (57) —Б —Г—З–µ—В–Њ–Љ (52) –Є ќЊ' = —Е', –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞–µ–Љ, —З—В–Њ –і–ї—П –і–∞–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л (—Н–ї–µ–Ї—В—А–Њ–љ–∞)
,
(58)
–≥–і–µ
(59)
вАУ —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞, –Ї–Њ—В–Њ—А—Л–є —П–≤–ї—П–µ—В—Б—П —А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –њ—А–Њ–µ–Ї—Ж–Є–Є —Е–∞–Њ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –і–≤–Є–ґ–µ–љ–Є—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л (—Н–ї–µ–Ї—В—А–Њ–љ–∞) –љ–∞ –Њ—Б—М —Е –≤–Њ–Ј–ї–µ —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б–Є—Б—В–µ–Љ—Л (—А–Є—Б. 1).
ѕГex вАУ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –њ—А–Њ–µ–Ї—Ж–Є–Є —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –і–≤–Є–ґ—Г—Й–µ–є—Б—П —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л (—Н–ї–µ–Ї—В—А–Њ–љ–∞) –љ–∞ –Њ—Б—М —Е –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Б—А–µ–і–љ–µ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П (—В.–µ. —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б–Є—Б—В–µ–Љ—Л).
–° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л, –Є–Ј –≤—Л—А–∞–ґ–µ–љ–Є—П (58) —Б–ї–µ–і—Г–µ—В, —З—В–Њ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞ —Н—В–Њ –љ–µ –љ–µ–Ї–∞—П —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–∞—П –Ї–Њ–љ—Б—В–∞–љ—В–∞ (–≤—Л—Б—И–∞—П –і–∞–љ–љ–Њ—Б—В—М), –∞ –≤–µ–ї–Є—З–Є–љ–∞, –≤—Л—А–∞–ґ–∞–µ–Љ–∞—П —З–µ—А–µ–Ј —Г—Б—А–µ–і–љ–µ–љ–љ—Л–µ –њ–∞—А–∞–Љ–µ—В—А—Л —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞
,
(60)
–≥–і–µ –≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ:
ѕГ—Зx вАУ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –њ—А–Њ–µ–Ї—Ж–Є–Є –љ–∞ –Њ—Б—М —Е —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –і–≤–Є–ґ—Г—Й–µ–є—Б—П —З–∞—Б—В–Є—Ж—Л (¬Ђ—В–Њ—З–Ї–Є¬ї) –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Б—А–µ–і–љ–µ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П (—В.–µ. ¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б–Є—Б—В–µ–Љ—Л);
ѕД—З—Е вАУ —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞, –Ї–Њ—В–Њ—А—Л–є —П–≤–ї—П–µ—В—Б—П —А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –њ—А–Њ–µ–Ї—Ж–Є–Є –љ–∞ –Њ—Б—М —Е —Е–∞–Њ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –і–≤–Є–ґ–µ–љ–Є—П —З–∞—Б—В–Є—Ж—Л (¬Ђ—В–Њ—З–Ї–Є¬ї) –≤–Њ–Ј–ї–µ –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б–Є—Б—В–µ–Љ—Л;
m вАУ –Љ–∞—Б—Б–∞ —З–∞—Б—В–Є—Ж—Л (¬Ђ—В–Њ—З–Ї–Є¬ї).
–Я—А–Є —Н—В–Њ–Љ ƒІ вАУ ¬Ђ–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞¬ї, –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П –Ї–Њ–љ—Б—В–∞–љ—В–Њ–є –ї–Є—И—М –≤ —В–Њ–Љ —Б–Љ—Л—Б–ї–µ, —З—В–Њ –Њ–љ–∞ –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –Љ–∞—Б—И—В–∞–±–Њ–≤ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, —В—А–Є –њ–∞—А–∞–Љ–µ—В—А–∞ m, ѕД—З—Е –Є ѕГ—Зx —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –±–ї—Г–ґ–і–∞—О—Й–µ–є (–±–µ–Ј –і–Є—Б—Б–Є–њ–∞—Ж–Є–Є) —З–∞—Б—В–Є—Ж—Л (–Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї) –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В—П—Е —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї –Љ–Њ–≥—Г—В –±—Л—В—М —В–Њ–ї—М–Ї–Њ —В–∞–Ї–Є–Љ–Є, —З—В–Њ –Є—Е —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ (60) –≤—Б–µ–≥–і–∞ –Њ—Б—В–∞–µ—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–Њ–є ƒІ = const.
–Ф–ї—П –Љ–љ–Њ–≥–Є—Е –њ—А–Є–ї–Њ–ґ–µ–љ–Є–є –±–Њ–ї–µ–µ –≤–∞–ґ–љ–Њ –љ–µ —Б–∞–Љ–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ (60), –∞ —Б–≤—П–Ј–∞–љ–љ–Њ–µ —Б –љ–Є–Љ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ (52), –Ї–Њ—В–Њ—А–Њ–µ –і–ї—П —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞—П —Г–і–Њ–±–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ
(61)
–Ю—В–Љ–µ—В–Є–Љ —Б–ї–µ–і—Г—О—Й–Є–µ –≤—Л–≤–Њ–і—Л:
1. –Ъ–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–є –њ–µ—А–µ—Е–Њ–і –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Ї –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –њ—А–Є–Љ–µ–љ–Є–Љ –љ–µ —В–Њ–ї—М–Ї–Њ –Ї –њ—А–Њ—Ж–µ—Б—Б–∞–Љ –Љ–Є—А–∞ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж, –∞ –Ї –ї—О–±—Л–Љ —Б–ї—Г—З–∞–є–љ—Л–Љ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–Љ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Є–Љ –њ—А–Њ—Ж–µ—Б—Б–∞–Љ, –Ї–∞–Ї –≤ –Љ–Є–Ї—А–Њ–Љ–Є—А–µ, —В–∞–Ї –Є –≤ –Љ–∞–Ї—А–Њ–Љ–Є—А–µ. –Э–∞–њ—А–Є–Љ–µ—А, –≤–µ—В–Ї–∞ –і–µ—А–µ–≤–∞, –њ–Њ—Б—В–Њ—П–љ–љ–Њ —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –Ї–Њ–ї–µ–±–ї—О—Й–∞—П—Б—П –≤–Њ–Ј–ї–µ –љ–µ–Ї–Њ–≥–Њ —Б—А–µ–і–љ–µ–≥–Њ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П (¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б–Є—Б—В–µ–Љ—Л) –њ–Њ–і –і–µ–є—Б—В–≤–Є–µ–Љ –±—Л—Б—В—А–Њ –Љ–µ–љ—П—О—Й–Є—Е –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–є –њ–Њ—А—Л–≤–Њ–≤ –≤–µ—В—А–∞, –≤–µ–і–µ—В —Б–µ–±—П –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ –њ–Њ–≤–µ–і–µ–љ–Є—О —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л –≤ ¬Ђ–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ¬ї. –Ъ–Њ–ї–µ–±–∞–љ–Є—П –≤–µ—В–Ї–Є —В–∞–Ї–ґ–µ –Є–Љ–µ–µ—В –і–Є—Б–Ї—А–µ—В–љ—Л–є (–Ї–≤–∞–љ—В–Њ–≤—Л–є) –љ–∞–±–Њ—А —Г—Б—А–µ–і–љ–µ–љ–љ—Л—Е —Б–Њ—Б—В–Њ—П–љ–Є–є –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є –њ–Њ—А—Л–≤–Њ–≤ –≤–µ—В—А–∞. –Я—А–Є —Б–ї–∞–±—Л—Е –њ–Њ—А—Л–≤–∞—Е –≤–µ—В—А–∞ –≤–µ—В–Ї–∞ –≤ –Њ—Б–љ–Њ–≤–љ–Њ–Љ –Ї–Њ–ї–µ–±–ї–µ—В—Б—П –≤–Њ–Ј–ї–µ —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї, –њ—А–Є —Н—В–Њ–Љ –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –µ–µ –Ї–Њ–љ—Ж–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ–Є—Б–∞–љ–Њ –≥–∞—Г—Б—Б–Њ–≤—Л–Љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ. –Я—А–Є –±–Њ–ї–µ–µ –Є–љ—В–µ–љ—Б–Є–≤–љ—Л—Е –њ–Њ—А—Л–≤–∞—Е –≤–µ—В—А–∞ –Ї–Њ–љ–µ—Ж –≤–µ—В–Ї–Є –≤ —Б—А–µ–і–љ–µ–Љ –≤—А–∞—Й–∞–µ—В—Б—П –њ–Њ –Ї—А—Г–≥—Г; –њ—А–Є –µ—Й–µ –±–Њ–ї—М—И–Є—Е –њ–Њ—А—Л–≤–∞—Е –≤–µ—В—А–∞ –µ–µ –Ї–Њ–љ–µ—Ж –≤ –Њ—Б–љ–Њ–≤–љ–Њ–Љ –Њ–њ–Є—Б—Л–≤–∞–µ—В –≤–Њ—Б—М–Љ–µ—А–Ї—Г, –Є —В.–і. –Т –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В —Б–Є–ї—Л –≤–µ—В—А–∞ –Ї–Њ–љ–µ—Ж –≤–µ—В–Ї–Є –Љ–Њ–ґ–µ—В –≤ —Б—А–µ–і–љ–µ–Љ –Њ–њ–Є—Б—Л–≤–∞—В—М –і–Є—Б–Ї—А–µ—В–љ—Л–є –љ–∞–±–Њ—А —Д–Є–≥—Г—А –Ы–Є—Б—Б–∞–ґ—Г. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–є —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ –љ–µ —П–≤–ї—П–µ—В—Б—П —Н–Ї—Б–Ї–ї—О–Ј–Є–≤–љ–Њ–є –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В—М—О –Љ–Є–Ї—А–Њ–Љ–Є—А–∞, –Њ–љ —В–∞–Ї–ґ–µ –њ—А–Є–Љ–µ–љ–Є–Љ –Є –Ї —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–Љ—Г –Њ–њ–Є—Б–∞–љ–Є—О –Љ–љ–Њ–≥–Є—Е —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –Љ–∞–Ї—А–Њ–Љ–Є—А–∞.
2. –Ъ–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–є –њ–µ—А–µ—Е–Њ–і –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —Б–Є—Б—В–µ–Љ—Л –Ї –µ–µ –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—О –њ—А–Є–Љ–µ–љ–Є–Љ –ї–Є—И—М –Ї —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–Љ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Є–Љ –њ—А–Њ—Ж–µ—Б—Б–∞–Љ. –Ґ–Њ –µ—Б—В—М –Ї —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ—Л–Љ –њ—А–Њ—Ж–µ—Б—Б–∞–Љ ¬Ђ–±–µ–Ј –њ–Њ—Б–ї–µ–і–µ–є—Б—В–≤–Є—П¬ї. –Ъ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ–Љ—Г –≤—Л–≤–Њ–і—Г –њ—А–Є—И–ї–Є –Ш. –Я—А–Є–≥–Њ–ґ–Є–љ –Є –Ш. –°—В–µ–љ–≥–µ—А—Б [10, 11], –њ–Њ–Ї–∞–Ј–∞–≤—И–Є–µ, —З—В–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–є —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ –Є–љ–≤–∞—А–Є–∞–љ—В–µ–љ –≤–Њ –≤—А–µ–Љ–µ–љ–Є –њ–Њ –њ—А–Є—З–Є–љ–µ –Њ—В—Б—Г—В—Б—В–≤–Є—П –њ–Њ—Б–ї–µ–і–µ–є—Б—В–≤–Є—П.
3. –Я—А–Є–≤–µ–і–µ–љ–љ—Л–є –Ј–і–µ—Б—М –∞–ї–≥–Њ—А–Є—В–Љ –њ–µ—А–µ—Е–Њ–і–∞ –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П ѕБ(ќЊi) –Ї –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г ѕБ(mќЊпВҐi) –Є –Њ–±—А–∞—В–љ–Њ –њ–Њ–ї—Г—З–∞–µ—В—Б—П –њ—А–Є –Ї–Њ–љ–Ї—А–µ—В–љ–Њ–Љ –≤–Є–і–µ ќі-—Д—Г–љ–Ї—Ж–Є–Є (33), —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–µ —Б–Њ–і–µ—А–ґ–∞–љ–Є–µ –Ї–Њ—В–Њ—А–Њ–є –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ –Љ–∞—А–Ї–Њ–≤–Њ—Б—В–Є –Є—Б—Е–Њ–і–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞.
4. –Э–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –≤—Л—И–µ–Є–Ј–ї–Њ–ґ–µ–љ–љ–Њ–≥–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Я–†–Т ѕБ(ќЊi'') - –≤—В–Њ—А–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –Є—Б—Е–Њ–і–љ–Њ–≥–Њ, –њ–Њ –Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ –і–≤–∞–ґ–і—Л –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ, —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –Ф–ї—П —Н—В–Њ–≥–Њ –≤ –Ї–∞—З–µ—Б—В–≤–µ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Б–ї–µ–і—Г–µ—В —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М –љ–µ —Б–∞–Љ –њ—А–Њ—Ж–µ—Б—Б пБЄ (t), –∞ –µ–≥–Њ –њ–µ—А–≤–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П пБЄпВҐ(t) = пВґпБЄ(t)/пВґt. –Ґ–Њ–≥–і–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –≤—В–Њ—А–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ–Њ—Б—А–µ–і—Б—В–≤–Њ–Љ —В–Њ–є –ґ–µ –њ—А–Њ—Ж–µ–і—Г—А—Л (45) вАУ (48), —В–Њ–ї—М–Ї–Њ –њ—А–Є —Н—В–Њ–Љ –≤–Љ–µ—Б—В–Њ ѕБ(ќЊi) –≤ (45) –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ–Њ–і—Б—В–∞–≤–Є—В—М —Г–ґ–µ ѕБ(ќЊпВҐi).
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ–∞ –Я–†–Т ѕБ(ќЊi(n)) –ї—О–±–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є n —А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Б –њ–Њ–Љ–Њ—Й—М—О —Б–ї–µ–і—Г—О—Й–µ–є —А–µ–Ї—Г—А—А–µ–љ—В–љ–Њ–є –њ—А–Њ—Ж–µ–і—Г—А—Л:
;
(62)
;
(63)
;
(64)
(65)
–≥–і–µ
,
(66)
вАУ –і–Є—Б–њ–µ—А—Б–Є—П
–Є —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є nвАУ1
—А–∞–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ
–њ—А–Њ—Ж–µ—Б—Б–∞.
5. –Я—А–Њ—Ж–µ–і—Г—А–∞ (45) вАУ (48) –њ–Њ–ї–љ–Њ—Б—В—М—О –∞–љ–∞–ї–Њ–≥–Є—З–љ–∞—П –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є –њ—А–Њ—Ж–µ–і—Г—А–µ –њ–µ—А–µ—Е–Њ–і–∞ –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї –µ–µ –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—О, –њ–Њ–ї—Г—З–µ–љ–∞ –Ј–і–µ—Б—М –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є –Њ–±—Л—З–љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞, —В.–µ. –±–µ–Ј –њ—А–Є–≤–ї–µ—З–µ–љ–Є—П —Д–µ–љ–Њ–Љ–µ–љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е –њ—А–Є–љ—Ж–Є–њ–Њ–≤ –Ї–Њ—А–њ—Г—Б–Ї—Г–ї—П—А–љ–Њ-–≤–Њ–ї–љ–Њ–≤–Њ–≥–Њ –і—Г–∞–ї–Є–Ј–Љ–∞ –Ы—Г–Є –і–µ –С—А–Њ–є–ї—П. –Ґ–µ–Љ —Б–∞–Љ—Л–Љ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ –њ—А–Њ—Ж–µ—Б—Б—Л –Є —Б–Њ–±—Л—В–Є—П, –њ—А–Њ–Є—Б—Е–Њ–і—П—Й–Є–µ –≤ –Љ–Є—А–µ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж, –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л –њ—А–Њ—Ж–µ—Б—Б–∞–Љ –Љ–∞–Ї—А–Њ–Љ–Є—А–∞, –Є –і–ї—П –Є—Е –Њ–±—К—П—Б–љ–µ–љ–Є—П –≤–Њ–≤—Б–µ –љ–µ —В—А–µ–±—Г–µ—В—Б—П –њ—А–Є–≤–ї–µ—З–µ–љ–Є–µ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е –≥–Є–њ–Њ—В–µ–Ј. –С–µ–Ј –њ—А–Є–≤–ї–µ—З–µ–љ–Є—П –Є–і–µ–Є –Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–Є –≤–Њ–ї–љ –Љ–∞—В–µ—А–Є–Є –і–µ –С—А–Њ–є–ї—П –Љ–Њ–ґ–љ–Њ –Њ–±—К—П—Б–љ–Є—В—М –Є –і–Є—Д—А–∞–Ї—Ж–Є—О —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е —З–∞—Б—В–Є—Ж –љ–∞ –Ї—А–Є—Б—В–∞–ї–ї–Є—З–µ—Б–Ї–Є—Е —А–µ—И–µ—В–Ї–∞—Е —В–≤–µ—А–і—Л—Е –≤–µ—Й–µ—Б—В–≤. –Ю—В—Б—Л–ї–∞–µ–Љ, –љ–∞–њ—А–Є–Љ–µ—А, –Ї –њ. 2.9.6 –≤ –Ј–µ–ї–µ–љ–Њ–є —З–∞—Б—В–Є –Р–ї–≥–µ–±—А—Л —Б–Є–≥–љ–∞—В—Г—А [3], –≥–і–µ –њ–Њ–ї—Г—З–µ–љ–∞ —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П —А–∞—Б—З—С—В–∞ –Њ–±—К–µ–Љ–љ–Њ–є –і–Є–∞–≥—А–∞–Љ–Љ—Л (–Є–љ–і–Є–Ї–∞—В—А–Є—Б—Л) —А–∞—Б—Б–µ—П–љ–Є—П —З–∞—Б—В–Є—Ж –љ–∞ –Љ–љ–Њ–≥–Њ—Б–ї–Њ–є–љ–Њ–є –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Њ–є —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ї—А–Є—Б—В–∞–ї–ї–∞ (—А–Є—Б. 3), —Б–Њ–≤–њ–∞–і–∞—О—Й–∞—П —Б —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є –і–∞–љ–љ—Л–Љ–Є.
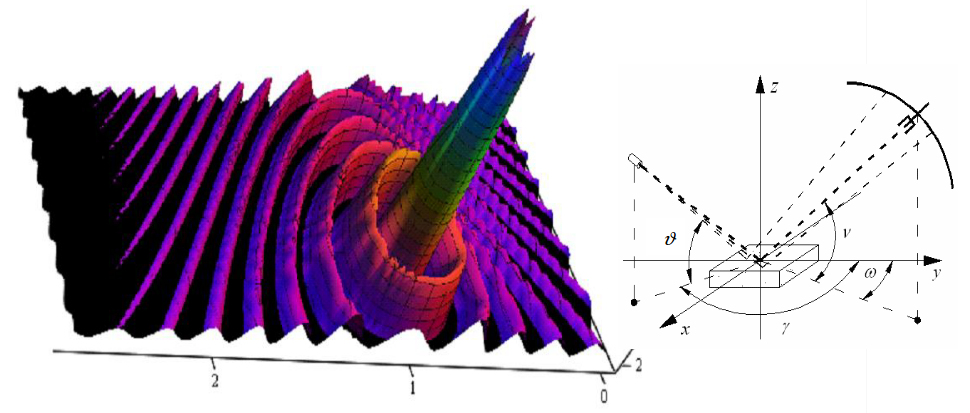
–†–Є—Б. 3. –Ф–Є–∞–≥—А–∞–Љ–Љ–∞ (–Є–љ–і–Є–Ї–∞—В—А–Є—Б–∞) —А–∞—Б—Б–µ—П–љ–Є—П —З–∞—Б—В–Є—Ж (—Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤) –љ–∞ –Љ–љ–Њ–≥–Њ—Б–ї–Њ–є–љ–Њ–є –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Њ–є —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—П—Е –Ї—А–Є—Б—В–∞–ї–ї–∞, —А–∞—Б—Б—З–Є—В–∞–љ–љ–∞—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ [3, 14]
,
–њ—А–Є —Г–≥–ї–µ –њ–∞–і–µ–љ–Є—П —З–∞—Б—В–Є—Ж –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Ї—А–Є—Б—В–∞–ї–ї–∞ пБК = 45–Њ –Є –∞–Ј–Є–Љ—Г—В–∞–ї—М–љ–Њ–Љ —Г–≥–ї–µ пБІ = 0–Њ
r–Ї–Њ—А = 0,0000000001 = 10вАУ10, l1 = 0,000000001 = 10вАУ9, n1 = 1940,
–≥–і–µ
–Є
k–Ї = r–Ї–Њ—А n12/ (0,066 l2),
–Ј–і–µ—Б—М:
l2 вАУ —В–Њ–ї—Й–Є–љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Љ–Њ–љ–Њ–Ї—А–Є—Б—В–∞–ї–ї–∞, –Њ—В—А–∞–ґ–∞—О—Й–µ–≥–Њ –њ—Г—З–Њ–Ї —Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤ l2 = n1l1 (–≥–і–µ l1вАУ —В–Њ–ї—Й–Є–љ–∞ –Њ–і–љ–Њ–≥–Њ —Б–ї–Њ—П, —В. –µ. –Њ–і–љ–Њ–є —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є; n1 вАУ —З–Є—Б–ї–Њ —Б–ї–Њ–µ–≤, —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ —Г—З–∞—Б—В–≤—Г—О—Й–Є—Е –≤ —А–∞—Б—Б–µ—П–љ–Є–Є —Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤);
r–Ї–Њ—А вАУ —Г—Б—А–µ–і–љ–µ–љ–љ—Л–є —А–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л –Њ–і–љ–Њ–є —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ф–ї—П –Љ–Њ–љ–Њ–Ї—А–Є—Б—В–∞–ї–ї–∞ —Г –≤—Б–µ—Е —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–µ–є r–Ї–Њ—А –Њ–і–Є–љ –Є —В–Њ—В –ґ–µ –Є –њ–Њ —Б—Г—В–Є –Њ–Ј–љ–∞—З–∞–µ—В —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ–µ —Б–µ—З–µ–љ–Є–µ —А–∞—Б—Б–µ—П–љ–Є—П –∞—В–Њ–Љ–∞–Љ–Є –Ї—А–Є—Б—В–∞–ї–ї–∞ —Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤.
4. –Ъ–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –Є–Љ–њ—Г–ї—М—Б–∞ —З–∞—Б—В–Є—Ж—Л
–Э–∞–њ–Њ–Љ–љ–Є–Љ —Б–љ–∞—З–∞–ї–∞ –Њ —Б–≤–Њ–є—Б—В–≤–∞—Е –Є–љ—В–µ–≥—А–∞–ї–∞ –Ф–Є—А–Є—Е–ї–µ, —Д–Є–≥—Г—А–Є—А—Г—О—Й–µ–≥–Њ –≤ —В–µ–Њ—А–Є–Є –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ –§—Г—А—М–µ –Є —В–µ–Њ—А–Є–Є –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є [5]:
,
(67)
–≥–і–µ
(68)
- –Њ–і–љ–∞ –Є–Ј —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–µ–є ќі-—Д—Г–љ–Ї—Ж–Є–Є, –Њ—В–≤–µ—З–∞—О—Й–∞—П —Г—Б–ї–Њ–≤–Є—П–Љ
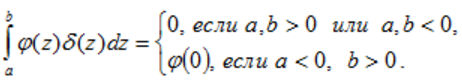
(69)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–∞–і–Є —Б–Њ–Ї—А–∞—Й–µ–љ–Є—П –≤—Л–Ї–ї–∞–і–Њ–Ї —Б–ї—Г—З–∞–є –Њ–і–љ–Њ–≥–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П –Є –і–Њ–Ї–∞–ґ–µ–Љ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В—М —А–∞–≤–µ–љ—Б—В–≤–∞ [5]
(70)
–≥–і–µ
n вАУ —Ж–µ–ї–∞—П, –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–∞—П —Б—В–µ–њ–µ–љ—М;
вАУ
—Г—Б—А–µ–і–љ–µ–љ–Є–µ
–њ–Њ –≤—А–µ–Љ–µ–љ–Є (–Є–ї–Є –њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є—П–Љ) –≤–Њ–Ј–≤–µ–і–µ–љ–љ–Њ–є
–≤ —Б—В–µ–њ–µ–љ—М n
–Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –Є–Љ–њ—Г–ї—М—Б–∞ —А—Еn
=
(m¬ЈпВґx/пВґt)n
=
(mx„≥)n;
вАУ –њ–ї–Њ—В–љ–Њ—Б—В–Є
—А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (–Я–Р–Т), –Ї–Њ—В–Њ—А—Л–µ
–≤–≤–Њ–і—П—В—Б—П –Ї–∞–Ї (24) [
]
–Є (48) [
],
–Є —Б–≤—П–Ј–∞–љ—Л –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є (–њ—А–Є —Г—Б–ї–Њ–≤–Є–Є
—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ—Б—В–Є –Є –Љ–∞—А–Ї–Њ–≤–Њ—Б—В–Є —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ
–њ—А–Њ—Ж–µ—Б—Б–∞), —Б–Њ–≥–ї–∞—Б–љ–Њ (46) –Є (47), –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П–Љ–Є
–§—Г—А—М–µ:
;
(71)
;
;
(72)
,
–≥–і–µ –њ–∞—А–∞–Љ–µ—В—А ќЈ—З –Њ–њ—А–µ–і–µ–ї–µ–љ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ (61)
.
(73)
–Ф–ї—П –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞ –њ–Њ–і—Б—В–∞–≤–Є–Љ –≤ (70) –≤–Љ–µ—Б—В–Њ ѕИ(—Аx) –Є ѕИ*(—Аx) –Є—Е –≤—Л—А–∞–ґ–µ–љ–Є—П —З–µ—А–µ–Ј –Є–љ—В–µ–≥—А–∞–ї—Л (71) [5]:
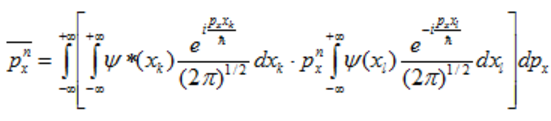 (74)
(74)
–Э–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ–є –њ—А–Њ–≤–µ—А–Ї–Њ–є –ї–µ–≥–Ї–Њ —Г–±–µ–і–Є—В—М—Б—П, —З—В–Њ
.
(75)
–Я–Њ–і—Б—В–∞–≤–ї—П—П (75) –≤ (74) –њ–Њ–ї—Г—З–Є–Љ:
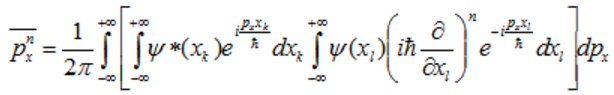 .
(76)
.
(76)
–Я—А–Њ–Є–љ—В–µ–≥—А–Є—А—Г–µ–Љ –≤—В–Њ—А–Њ–є –Є–љ—В–µ–≥—А–∞–ї –≤ –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є n —А–∞–Ј –њ–Њ —З–∞—Б—В—П–Љ, –њ—А–Є—З–µ–Љ –±—Г–і–µ–Љ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—В—М, —З—В–Њ ѕИ(x) –Є –µ–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –Њ–±—А–∞—Й–∞—О—В—Б—П –≤ –љ—Г–ї—М –љ–∞ –≥—А–∞–љ–Є—Ж–∞—Е –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П x = ¬± вИЮ. –Т—Л–њ–Њ–ї–љ—П—П –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ, –љ–∞–є–і–µ–Љ [5]
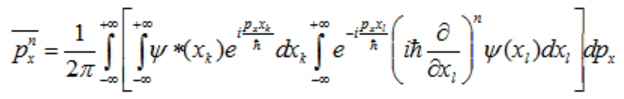 (77)
(77)
–Я–µ—А–µ–Љ–µ–љ–Є–Љ –њ–Њ—А—П–і–Њ–Ї –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –Є –±—Г–і–µ–Љ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞—В—М —Б–љ–∞—З–∞–ї–∞ –њ–Њ px [5]:
(78)
–Т–≤–µ–і–µ–Љ —В–µ–њ–µ—А—М –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ ќЊ= —Аx /h, z = xk вАУ xl. –Т—Л–њ–Њ–ї–љ—П—П –≤ –њ–Њ—Б–ї–µ–і–љ–µ–Љ –Є–љ—В–µ–≥—А–∞–ї–µ –≤ (78) –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –њ–Њ ќЊ –≤ –Ї–Њ–љ–µ—З–љ—Л—Е –њ—А–µ–і–µ–ї–∞—Е –Њ—В вАУ k –і–Њ + k, –∞ –Ј–∞—В–µ–Љ, –њ–µ—А–µ—Е–Њ–і—П –Ї –њ—А–µ–і–µ–ї—Г k вЖТ вИЮ, –і–∞–љ–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ [5]
(79)
–Э–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є —Б–≤–Њ–є—Б—В–≤ ќі-—Д—Г–љ–Ї—Ж–Є–Є (69) (a = вАУвИЮ; b = +вИЮ), ѕИ(z) = ѕИ*(x+z) –Є–Љ–µ–µ–Љ [5]
(80)
–Є–ї–Є
(81)
–≥–і–µ
(82)
(u вАУ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–µ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ), —В–µ–Љ —Б–∞–Љ—Л–Љ –і–Њ–Ї–∞–Ј–∞–љ–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ (70).
–Э–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є (71) –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М
(83)
–Ю–±–Њ–±—Й–µ–љ–Є–µ –љ–∞ —В—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П —Б–≤–Њ–і–Є—В—Б—П –Ї —Г–≤–µ–ї–Є—З–µ–љ–Є—О —З–Є—Б–ї–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–є [5].
5. –Т—Л–≤–Њ–і –Њ–±–Њ–±—Й–µ–љ–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞
–Т–µ—А–љ–µ–Љ—Б—П –Ї —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—О —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П (15)
(84)
–Ї–Њ—В–Њ—А–Њ–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–Љ—Г —Б–Њ—Б—В–Њ—П–љ–Є—О —З–∞—Б—В–Є—Ж—Л (–Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї), —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –±–ї—Г–ґ–і–∞—О—Й–µ–є –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї —Б –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –њ–Њ–ї–љ–Њ–є –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —Н–љ–µ—А–≥–Є–µ–є –Х (—А–Є—Б. 1).
–Я—А–µ–і—Б—В–∞–≤–Є–Љ —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–µ –і–µ–є—Б—В–≤–Є–µ (84) –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–Љ –≤–Є–і–µ. –Ф–ї—П —Н—В–Њ–≥–Њ –≤—Л–њ–Њ–ї–љ–Є–Љ —Б–ї–µ–і—Г—О—Й–Є–µ –Њ–њ–µ—А–∞—Ж–Є–Є.
1. –Ч–∞–њ–Є—И–µ–Љ –Я–†–Т ѕБ(—Е) –≤ –≤–Є–і–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –і–≤—Г—Е –њ–ї–Њ—В–љ–Њ—Б—В–µ–є –∞–Љ–њ–ї–Є—В—Г–і—Л –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (–Я–Р–Т) ѕИ(—Е):
(85)
–≥–і–µ
,
(86)
(87)
2. –Т–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ–Љ —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –Є–Љ–њ—Г–ї—М—Б–∞, –≤–Њ–Ј–≤–µ–і–µ–љ–љ–Њ–≥–Њ –≤ —Б—В–µ–њ–µ–љ—М n (81). –Я—А–Є —Н—В–Њ–Љ –≤ —З–∞—Б—В–љ–Њ—Б—В–Є –Є–Љ–µ–µ–Љ
,
(88)
–Э–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –≤ –њ—Г–љ–Ї—В–∞—Е 3 –Є 4, —В–∞–Ї–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ —В–Њ–ї—М–Ї–Њ –і–ї—П —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ (–≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –і–ї—П —Е–∞–Њ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –±–µ–Ј –њ–Њ—Б–ї–µ–і–µ–є—Б—В–≤–Є—П –і–≤–Є–ґ–µ–љ–Є—П –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї –≤–Њ–Ј–ї–µ —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї).
3. –Ш—Б–њ–Њ–ї—М–Ј—Г—П (88) –њ—А–µ–і—Б—В–∞–≤–Є–Љ —Г—Б—А–µ–і–љ–µ–љ–љ—Г—О –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї—Г—О —Н–љ–µ—А–≥–Є—О ¬Ђ—В–Њ—З–Ї–Є¬ї (13) –≤ –≤–Є–і–µ
(90)
–∞ –µ–µ —Г—Б—А–µ–і–љ–µ–љ–љ–∞—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П (14) —Б —Г—З—С—В–Њ–Љ (85) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
(89)
–Я—А–Њ–≤–µ—А–Ї–Њ–є –ї–µ–≥–Ї–Њ —Г–±–µ–і–Є—В—М—Б—П –≤ —В–Њ–Љ, —З—В–Њ
(100)
–Є–ї–Є —Б —Г—З–µ—В–Њ–Љ (86, 87)
(101)
4. –Я–Њ–і—Б—В–∞–≤–ї—П—П –≤—Л—А–∞–ґ–µ–љ–Є—П (90), (89) –Є (101) –≤ (84), –њ–Њ–ї—Г—З–Є–Љ –Ј–∞–њ–Є—Б—М —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П –±–ї—Г–ґ–і–∞—О—Й–µ–є ¬Ђ—В–Њ—З–Ї–Є¬ї –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–Љ –≤–Є–і–µ
(102)
–Є–ї–Є
(103)
–£—Б–ї–Њ–≤–Є–µ —Н–Ї—Б—В—А–µ–Љ–∞–ї—М–љ–Њ—Б—В–Є —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П (103) —В—А–µ–±—Г–µ—В –Њ–±—А–∞—Й–µ–љ–Є—П –≤ –љ–Њ–ї—М –µ–≥–Њ –њ–µ—А–≤–Њ–є –≤–∞—А–Є–∞—Ж–Є–Є (–≤—Б–µ –њ–Њ—Б–ї–µ–і—Г—О—Й–Є–µ –Њ–њ–µ—А–∞—Ж–Є–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ—Г –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –Є—Б—З–Є—Б–ї–µ–љ–Є—П [12])
(104)
–≠–Ї—Б—В—А–µ–Љ–∞–ї—М —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–∞ (104), —В. –µ. —Д—Г–љ–Ї—Ж–Є—П пБє (x,t), –њ—А–Є –Ї–Њ—В–Њ—А–Њ–є —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–µ –і–µ–є—Б—В–≤–Є–µ (104) –њ—А–Є–љ–Є–Љ–∞–µ—В —Н–Ї—Б—В—А–µ–Љ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –≠–є–ї–µ—А–∞ вАУ –Я—Г–∞—Б—Б–Њ–љ–∞ [12]. –Ф–∞–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –ї–∞–≥—А–∞–љ–ґ–Є–∞–љ–∞ L, —П–≤–ї—П—О—Й–µ–≥–Њ—Б—П –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ—Л–Љ –≤—Л—А–∞–ґ–µ–љ–Є–µ–Љ –≤ —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–µ –і–µ–є—Б—В–≤–Є—П
–≥–і–µ
z
=пБє
(x,
t),
(105)
–Є–Љ–µ–µ—В –≤–Є–і [12]
(106)
–Ј–і–µ—Б—М
(107)
вАУ –њ–Њ–ї–љ–∞—П —З–∞—Б—В–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ —Е.
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ
(108)
–Є —В. –і.
–Ш—Б–њ–Њ–ї—М–Ј—Г—П –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –Є–Ј —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П (104), –Њ–њ—А–µ–і–µ–ї–Є–Љ
–Я–Њ–і—Б—В–∞–≤–ї—П—П —Н—В–Є –≤—Л—А–∞–ґ–µ–љ–Є—П –≤ (106), –њ–Њ–ї—Г—З–Є–Љ –Є—Б–Ї–Њ–Љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Н–Ї—Б—В—А–µ–Љ–∞–ї–Є ѕИ (—Е,t) —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–∞ —Г—Б—А–µ–і–љ—С–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П (104)
(109)
–≥–і–µ
пБє (x,t)пБє пА™(x,t) = |пБє (x)| 2 = пБ≤(x)
вАУ –Я–†–Т –њ—А–Њ–µ–Ї—Ж–Є–Є –љ–∞ –Њ—Б—М —Е –Љ–µ—Б—В–∞ –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї, –±–ї—Г–ґ–і–∞—О—Й–µ–є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї —В–∞–Ї, —З—В–Њ –µ–µ –њ–Њ–ї–љ–∞—П –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П E –≤—Б–µ–≥–і–∞ –Њ—Б—В–∞–µ—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є (–Х = const), –∞ —Б–∞–Љ–∞ –і–∞–љ–љ–∞—П –њ—А–Њ–µ–Ї—Ж–Є—П —Е (t) —П–≤–ї—П–µ—В—Б—П —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–Љ —Б–ї—Г—З–∞–є–љ—Л–Љ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Є–Љ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ.
–Ю–±–Њ–±—Й–µ–љ–Є–µ –љ–∞ —В—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П, —Б–≤–Њ–і—П—Й–µ–µ—Б—П –Ї —Г–≤–µ–ї–Є—З–µ–љ–Є—О —З–Є—Б–ї–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–є, –њ—А–Є —Н—В–Њ–Љ –Є–Љ–µ–µ–Љ
(110)
–≥–і–µ
r вАУ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А —Б –љ–∞—З–∞–ї–Њ–Љ –≤ ¬Ђ—Ж–µ–љ—В—А–µ¬ї –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П (r2 = x2 + y2 + z2) (—А–Є—Б.1).
–£—А–∞–≤–љ–µ–љ–Є–µ
(110) —П–≤–ї—П–µ—В—Б—П –љ–µ —З–µ–Љ –Є–љ—Л–Љ, –Ї–∞–Ї —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ
–®—А–µ–і–Є–љ–≥–µ—А–∞ (1) —Б –±–Њ—А–љ–Њ–≤—Б–Ї–Є–Љ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ–Љ
—Б–Љ—Л—Б–ї–∞ –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є
.
–Э–Њ –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ ¬Ђ–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞¬ї ƒІ
вАУ —Н—В–Њ –љ–µ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–∞—П –Ї–Њ–љ—Б—В–∞–љ—В–∞, –∞
–њ–∞—А–∞–Љ–µ—В—А (60), –≤—Л—А–∞–ґ–µ–љ–љ—Л–є —З–µ—А–µ–Ј —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ
—Г—Б—А–µ–і–љ–µ–љ–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ
—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ
—Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –Љ–∞—А–Ї–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞
,
–Х—Б–ї–Є –Њ–±–µ —З–∞—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є—П (110) —Б–Њ–Ї—А–∞—В–Є—В—М –љ–∞ ƒІ —В–Њ –њ–Њ–ї—Г—З–Є–Љ
–° —Г—З–µ—В–Њ–Љ (61) –Ф–∞–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А–Є–љ–Є–Љ–∞–µ—В
(111)
–≥–і–µ
,
(112)
–Ј–і–µ—Б—М
(113)
вАУ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–µ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –і–≤–Є–ґ—Г—Й–µ–є—Б—П —З–∞—Б—В–Є—Ж—Л (–Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є ¬Ђ—В–Њ—З–Ї–Є¬ї) –Њ—В —Г—Б–ї–Њ–≤–љ–Њ–≥–Њ ¬Ђ—Ж–µ–љ—В—А–∞¬ї (—А–Є—Б. 1);
(114)
-
–≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є —Г—Б—А–µ–і–љ–µ–љ–љ—Л–є —А–∞–і–Є—Г—Б –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є (—В–Њ—З–љ–µ–µ –∞–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Є) —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞.
–£—А–∞–≤–љ–µ–љ–Є–µ (111) –±—Г–і–µ–Љ –љ–∞–Ј—Л–≤–∞—В—М –Њ–±–Њ–±—Й—С–љ–љ—Л–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –®—А–µ–і–Є–љ–≥–µ—А–∞.
–Я—А–µ–і–ї–Њ–ґ–µ–љ–љ—Л–є –≤ –і–∞–љ–љ–Њ–є —Б—В–∞—В—М–µ –њ–Њ–і—Е–Њ–і –њ–Њ–Ј–≤–Њ–ї–Є–ї –≤—Л–≤–µ—Б—В–Є –Њ—Б–љ–Њ–≤–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є, –Є—Б—Е–Њ–і—П –Є–Ј –њ—А–Є–љ—Ж–Є–њ–Њ–≤ –≤ –Ї–Њ—А–љ–µ –Њ—В–ї–Є—З–∞—О—Й–Є—Е—Б—П –Њ—В –Є–і–µ–є–љ—Л—Е —Г—Б—В–Њ–µ–≤ –љ–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В–Њ–≤. –Э–Њ —Б–∞–Љ–∞ –Ї–≤–∞–љ—В–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞, —Б–Њ–Ј–і–∞–љ–љ–∞—П –њ–ї–µ—П–і–Њ–є –≤–µ–ї–Є–Ї–Є—Е —Г—З–µ–љ—Л—Е, –Њ—В —Н—В–Њ–≥–Њ —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ –љ–µ –њ–Њ—Б—В—А–∞–і–∞–ї–Њ, –∞ —В–Њ–ї—М–Ї–Њ —Г–Ї—А–µ–њ–Є–ї–Є—Б—М –µ–µ –ї–Њ–≥–Є—З–µ—Б–Ї–Є–µ –Њ—Б–љ–Њ–≤–∞–љ–Є—П.
–Я–Њ–і–Њ–±–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –Љ–Њ–≥—Г—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ—Л –≤—Б–µ –Њ—Б–љ–Њ–≤–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –њ–Њ–ї—П: —Г—А–∞–≤–љ–µ–љ–Є–µ –Ъ–ї–µ–љ–∞-–У–Њ—А–і–Њ–љ–∞, —Г—А–∞–≤–љ–µ–љ–Є—П –Ф–Є—А–∞–Ї–∞, —Г—А–∞–≤–љ–µ–љ–Є—П –Ь–∞–Ї—Б–≤–µ–ї–ї–∞ –Є —В. –і. –Р–ї–≥–Њ—А–Є—В–Љ –Є—Е –≤—Л–≤–Њ–і–∞ –∞–љ–∞–ї–Њ–≥–Є—З–µ–љ –њ–Њ–і—Е–Њ–і—Г, –њ—А–Є–≤–µ–і–µ–љ–љ–Њ–Љ—Г –≤ –і–∞–љ–љ–Њ–є —Б—В–∞—В—М–µ:
1) –Ј–∞–њ–Є—Б—Л–≤–∞–µ—В—Б—П –і–µ—В–µ—А–Љ–Є–љ–Є—Б—В—Б–Ї–Њ–µ –і–µ–є—Б—В–≤–Є–µ —Б–Є—Б—В–µ–Љ—Л;
2) –і–∞–љ–љ–Њ–µ –і–µ–є—Б—В–≤–Є–µ —Г—Б—А–µ–і–љ—П–µ—В—Б—П;
3) –≤—Б–µ —Г—Б—А–µ–і–љ–µ–љ–љ—Л–µ —Б–ї–∞–≥–∞–µ–Љ—Л–µ –≤ –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В—Б—П —З–µ—А–µ–Ј –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є ѕБ(—Е) –Є/–Є–ї–Є ѕБ(px);
4) –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В—Б—П –њ–µ—А–µ—Е–Њ–і –≤—Б–µ—Е —Б–ї–∞–≥–∞–µ–Љ—Л—Е –ї–∞–≥—А–∞–љ–ґ–Є–∞–љ–∞ —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–µ –Є–ї–Є –≤ –Є–Љ–њ—Г–ї—М—Б–љ–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ;
5) –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П —Н–Ї—Б—В—А–µ–Љ–∞–ї–Є –њ–Њ–ї—Г—З–Є–≤—И–µ–≥–Њ—Б—П —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–∞ (—Г—Б—А–µ–і–љ–µ–љ–љ–Њ–≥–Њ –і–µ–є—Б—В–≤–Є—П) –њ–Њ —Б—А–µ–і—Б—В–≤–∞–Љ –Љ–µ—В–Њ–і–Њ–≤ –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –Є—Б—З–Є—Б–ї–µ–љ–Є—П.
–Ч–љ–∞—З–Є–Љ–Њ—Б—В—М –њ—А–Є–≤–µ–і–µ–љ–љ–Њ–≥–Њ –Ј–і–µ—Б—М –≤—Л–≤–Њ–і–∞ –Њ–±–Њ–±—Й—С–љ–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ (111) –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ:
- —Б—В–∞–љ–Њ–≤–Є—В—Б—П –њ–Њ–љ—П—В–љ—Л–Љ, –Ї –Ї–∞–Ї–Є–Љ —П–≤–ї–µ–љ–Є—П–Љ –Љ–Є–Ї—А–Њ- –Є –Љ–∞–Ї—А–Њ–Љ–Є—А–∞ –Њ–љ–Њ –Њ—В–љ–Њ—Б–Є—В—Б—П, –Ї–∞–Ї–Њ–≤—Л –≥—А–∞–љ–Є—Ж—Л –Є —Г—Б–ї–Њ–≤–Є—П –µ–≥–Њ –њ—А–Є–Љ–µ–љ–µ–љ–Є—П.
- –Њ—В–њ–∞–ї–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М –≤ –њ—А–Є–≤–ї–µ—З–µ–љ–Є–Є ¬Ђ–њ—А–Є–љ—Ж–Є–њ–∞ –љ–µ–Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ—Б—В–Є¬ї –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ –Є –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є –Њ ¬Ђ–≤–Њ–ї–љ–∞—Е –Љ–∞—В–µ—А–Є–Є¬ї –і–µ –С—А–Њ–є–ї—П, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ—А–Є –≤—Л–≤–Њ–і–µ —Г—А–∞–≤–љ–µ–љ–Є—П (111) –њ–Њ–ї—Г—З–µ–љ–∞ –њ—А–Њ—Ж–µ–і—Г—А–∞ (45) - (48), –њ–Њ–ї–љ–Њ—Б—В—М—О –∞–љ–∞–ї–Њ–≥–Є—З–љ–∞—П –њ–µ—А–µ—Е–Њ–і—Г –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є (–≤ —В.—З. –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є) —Б–Є—Б—В–µ–Љ—Л –Ї –µ–µ –Є–Љ–њ—Г–ї—М—Б–љ–Њ–Љ—Г –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—О, –±–µ–Ј —Н—В–Є—Е –Ї–≤–∞–љ—В–Њ–≤–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є—Е –њ—А–Є–љ—Ж–Є–њ–Њ–≤.
- ¬Ђ–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞¬ї ƒІ –њ—А–Є–Њ–±—А–µ—В–∞–µ—В –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —З–µ—А–µ–Ј —Г—Б—А–µ–і–љ–µ–љ–љ—Л–µ –њ–∞—А–∞–Љ–µ—В—А—Л –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞;
- —П–≤–ї–µ–љ–Є—П –Љ–Є–Ї—А–Њ–Љ–Є—А–∞ –Њ–Ї–∞–Ј—Л–≤–∞—О—В—Б—П –њ–Њ–і–Њ–±–љ—Л–Љ–Є —П–≤–ї–µ–љ–Є—П–Љ –Љ–∞–Ї—А–Њ–Љ–Є—А–∞. –£—А–∞–≤–љ–µ–љ–Є–µ (111) –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ —Е–Њ—А–Њ—И–Њ –Њ–њ–Є—Б—Л–≤–∞–µ—В —Г—Б—А–µ–і–љ–µ–љ–љ–Њ–µ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ, —П–і—А–∞ –≤ —Ж–Є—В–Њ–њ–ї–∞–Ј–Љ–µ –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є –Ї–ї–µ—В–Ї–Є, –Љ–ї–∞–і–µ–љ—Ж–∞ –≤ –≤–Њ–ї—М–µ—А–µ, —П–і—А–∞ –≤ –љ–µ–і—А–∞—Е –њ–ї–∞–љ–µ—В—Л, —В–Є–≥—А–∞ –≤ –Ї–ї–µ—В–Ї–µ, –Љ—Г—Е–Є –≤ –±–∞–љ–Ї–µ –Є —В.–і. –Т—Б–µ —Н—В–Є –њ—А–Њ—Ж–µ—Б—Б—Л –Њ–±–ї–∞–і–∞—О—В –і–Є—Б–Ї—А–µ—В–љ—Л–Љ –љ–∞–±–Њ—А–Њ–Љ —Г—Б—А–µ–і–љ–µ–љ–љ—Л—Е —Б–Њ—Б—В–Њ—П–љ–Є–є, —Б–≤–Њ–є—Б—В–≤–µ–љ–љ—Л—Е –Ј–∞–Љ–Ї–љ—Г—В—Л–Љ —Б–Є—Б—В–µ–Љ–∞–Љ;
- –≤–Њ–Ј–≤—А–∞—Й–∞—О—В—Б—П –Ї —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—О –Њ–±—К–µ–Љ –Є —В—А–∞–µ–Ї—В–Њ—А–Є—П –±–ї—Г–ґ–і–∞—О—Й–µ–є —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–є —З–∞—Б—В–Є—Ж—Л. –° –≤–Њ–Ј—А–∞—Й–µ–љ–Є–µ–Љ –љ–∞–≥–ї—П–і–љ–Њ—Б—В–Є, —Д–Є–Ј–Є–Ї–∞ –Љ–Є–Ї—А–Њ–Љ–Є—А–∞ –≤–љ–Њ–≤—М –њ—А–Є–Њ–±—А–µ—В–∞–µ—В –њ—А–Є–≤—Л—З–љ—Г—О –ї–Њ–≥–Є—З–µ—Б–Ї—Г—О ¬Ђ–њ–Њ—З–≤—Г –њ–Њ–і –љ–Њ–≥–∞–Љ–Є¬ї;
- –Њ–±–Њ–±—Й—С–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ (111) –љ–µ —Б–Њ–і–µ—А–ґ–Є—В —А–∞–Ј–Љ–µ—А–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л вАУ –Љ–∞—Б—Б—Л —З–∞—Б—В–Є—Ж—Л m, –Є –Є–Ј-–Ј–∞ –Ї–Њ—В–Њ—А–Њ–є –њ—А–Є—Е–Њ–і–Є—В—М—Б—П –≤–≤–Њ–і–Є—В—М –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Г—О —А–∞–Ј–Љ–µ—А–љ—Г—О –Ї–Њ–љ—Б—В–∞–љ—В—Г вАУ –њ–Њ—Б—В–Њ—П–љ–љ—Г—О –Я–ї–∞–љ–Ї–∞ ƒІ. ¬Ђ–Ь–∞—Б—Б–∞¬ї —П–≤–ї—П–µ—В—Б—П (–њ–Њ –Љ–Њ–µ–Љ—Г –Љ–љ–µ–љ–Є—О) –Њ–і–љ–Њ–є –Є–Ј —Б–∞–Љ—Л—Е ¬Ђ—В–µ–Љ–љ—Л—Е¬ї —А–∞–Ј–Љ–µ—А–љ—Л—Е –≤–µ–ї–Є—З–Є–љ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є —Д–Є–Ј–Є–Ї–Є (—Б–Љ. –њ. 1.7.10 –≤ [2] –Є –≥–ї. 7 –≤ [3]). –Э–µ—Б–Њ–Љ–љ–µ–љ–љ–Њ, —З—В–Њ –≤ –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ–є —В–µ–Њ—А–Є–Є –њ–Њ–љ—П—В–Є–µ ¬Ђ–Љ–∞—Б—Б–∞¬ї –і–Њ–ї–ґ–љ–Њ –Њ—В—Б—Г—В—Б—В–≤–Њ–≤–∞—В—М, –Є –і–∞–љ–љ–∞—П —Б—В–∞—В—М—П - —Н—В–Њ –Њ–і–Є–љ –Є–Ј —И–∞–≥–Њ–≤ –≤ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є –Є—Б–Ї–Њ—А–µ–љ–µ–љ–Є—П –і–∞–љ–љ–Њ–є —А–∞–Ј–Љ–µ—А–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л –Є–Ј –љ–∞—И–Є—Е –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є –Њ –≤–µ—Й–µ—Б—В–≤–µ.
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –і–∞–љ–љ–∞—П —Б—В–∞—В—М—П –Љ–Њ–ґ–µ—В –≤–љ–µ—Б—В–Є –љ–µ–Ї–Њ—В–Њ—А—Г—О —П—Б–љ–Њ—Б—В—М –≤ —А–∞–Ј—А–µ—И–µ–љ–Є–µ —Б–њ–Њ—А–∞ –Љ–µ–ґ–і—Г –Э. –С–Њ—А–Њ–Љ –Є –Р. –≠–є–љ—И—В–µ–є–љ–Њ–Љ –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є ¬Ђ–≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є¬ї. –Э–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ –Р–ї—М–±–µ—А—В –≠–є–љ—И—В–µ–є–љ, –Ї–∞–Ї –Є –Љ–љ–Њ–≥–Є–µ –і—А—Г–≥–Є–µ —Д–Є–Ј–Є–Ї–Є —В–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є, –Њ—В–љ–Њ—Б–Є–ї—Б—П –Ї –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (—В–Њ—З–љ–µ–µ –Ї —Б—В–∞—В–Є—Б—В–Є–Ї–µ), –Ї–∞–Ї –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ–Љ—Г —Г–њ—А–Њ—Й–µ–љ–Є—О –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–њ–Є—Б–∞–љ–Є—П —Б–ї–Њ–ґ–љ–Њ–≥–Њ –њ–Њ–≤–µ–і–µ–љ–Є—П –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л (–љ–∞–њ—А–Є–Љ–µ—А, –±–ї—Г–ґ–і–∞—О—Й–µ–є —З–∞—Б—В–Є—Ж—Л), –љ–∞—Е–Њ–і—П—Й–µ–є—Б—П –њ–Њ–і –≤–ї–Є—П–љ–Є–µ–Љ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е, –љ–Њ –љ–µ—Б–≤—П–Ј–∞–љ–љ—Л—Е –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є —Д–∞–Ї—В–Њ—А–Њ–≤. –Э–Є–ї—М—Б –С–Њ—А –Є –µ–≥–Њ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є –Њ—В—Б—В–∞–Є–≤–∞–ї–Є –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ –Є–љ–Њ–є –њ–Њ–і—Е–Њ–і, —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М, –Ї–∞–Ї –Є—Б—Е–Њ–і–љ—Г—О, –њ–µ—А–≤–Є—З–љ—Г—О –і–∞–љ–љ–Њ—Б—В—М –њ—А–Є—А–Њ–і—Л –Љ–Є–Ї—А–Њ–Љ–Є—А–∞; –∞ –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л–µ —П–≤–ї–µ–љ–Є—П –Љ–∞–Ї—А–Њ–Љ–Є—А–∞, –њ–Њ –Љ–љ–µ–љ–Є—О –љ–µ–Њ–њ–Њ–Ј–Є—В–Є–≤–Є—Б—В–Њ–≤, –µ—Б—В—М —А–µ–Ј—Г–ї—М—В–∞—В —Г—Б—А–µ–і–љ–µ–љ–Є—П –Є–Ј–љ–∞—З–∞–ї—М–љ–Њ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ—Л—Е (—Б–ї—Г—З–∞–є–љ—Л—Е) —Б—Г–±–∞—В–Њ–Љ–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤. –Ф–∞–љ–љ–∞—П —Б—В–∞—В—М—П –љ–∞–њ–Є—Б–∞–љ–∞ —Б –њ–Њ–Ј–Є—Ж–Є–є –Р–ї—М–±–µ—А—В–∞ –≠–є–љ—И—В–µ–є–љ–∞, —З—В–Њ –Є –њ—А–Є–≤–µ–ї–Њ –Ї –≤—Л–≤–Њ–і—Г —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞. –Ю–і–љ–∞–Ї–Њ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В–Є —А–∞–і–Є —Б–ї–µ–і—Г–µ—В –Њ—В–Љ–µ—В–Є—В—М, —З—В–Њ, —Б—Г–і—П –њ–Њ –≤—Б–µ–Љ—Г, –Є–Љ–µ–µ—В—Б—П –Є –≤—В–Њ—А–Њ–є –≤—Л–≤–Њ–і –і–∞–љ–љ–Њ–≥–Њ –Њ—Б–љ–Њ–≤–Њ–њ–Њ–ї–∞–≥–∞—О—Й–µ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П, –Є—Б—Е–Њ–і—П –Є–Ј –њ—А–Є–љ—Ж–Є–њ–∞ —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞ –Є–љ—В–µ–≥—А–∞–ї–∞ —Н–љ—В—А–Њ–њ–Є–Є (—Б–Љ. –њ. 2.8.7 –≤ [3]) —Б–ї–Њ–ґ–љ–Њ —Д–ї—Г–Ї—В—Г–Є—А—Г—О—Й–µ–є —Б–Є—Б—В–µ–Љ—Л, —В.–µ. —Б –њ–Њ–Ј–Є—Ж–Є–є –Љ–љ–µ–љ–Є—П –Э–Є–ї—М—Б–∞ –С–Њ—А–∞ –љ–∞ –њ—А–Є—А–Њ–і—Г –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є. –Я–Њ –≤—Б–µ–є –≤–Є–і–Є–Љ–Њ—Б—В–Є, –і–µ—В–µ—А–Љ–Є–љ–Є–Ј–Љ –Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М вАУ —Н—В–Њ –њ—А–Њ—П–≤–ї–µ–љ–Є—П –µ–і–Є–љ–Њ–є –і—Г–∞–ї—М–љ–Њ—Б—В–Є, –ї–µ–ґ–∞—Й–µ–є –≤ –Њ—Б–љ–Њ–≤–∞–љ–Є—П—Е —Н—В–Њ–≥–Њ –Љ–Є—А–∞.
–Ю—Б–љ–Њ–≤–љ—Л–µ —В–µ–Ј–Є—Б—Л –і–∞–љ–љ–Њ–є —Б—В–∞—В—М–Є –±—Л–ї–Є –≤–њ–µ—А–≤—Л–µ —З–∞—Б—В–Є—З–љ–Њ –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ—Л –≤ –њ–Њ—А—П–і–Ї–µ –Њ–±—Б—Г–ґ–і–µ–љ–Є—П –≤ 1990 –≥. –≤ [13,14], –±–ї–∞–≥–Њ–і–∞—А—П –Љ–Њ–Є–Љ –љ–∞—Б—В–∞–≤–љ–Є–Ї–∞–Љ: –і.—В.–љ., –њ—А–Њ—Д–µ—Б—Б–Њ—А—Г –Р–ї—М–±–µ—А—В—Г –Р–љ–і—А–µ–µ–≤–Є—З—Г –Ъ—Г–Ј–љ–µ—Ж–Њ–≤—Г –Є –і.—Д-–Љ.–љ., –њ—А–Њ—Д–µ—Б—Б–Њ—А—Г –Р–љ–∞—В–Њ–ї–Є—О –Ш–≤–∞–љ–Њ–≤–Є—З—Г –Ъ–Њ–Ј–ї–Њ–≤—Г.
–°–Я–Ш–°–Ю–Ъ –Ы–Ш–Ґ–Х–†–Р–Ґ–£–†–Ђ
1. –Ы–∞–љ–і–∞—Г –Ы.–Ф., –Ы–Є—Д—И–Є—Ж –Х.–Ь. –Ь–µ—Е–∞–љ–Є–Ї–∞. вАУ –Ь.: –Э–∞—Г–Ї–∞, 1988, –°. 237.
2. –У–∞—Г—Е–Љ–∞–љ –Ь.–•. –Р–ї–≥–µ–±—А–∞ —Б–Є–≥–љ–∞—В—Г—А ¬Ђ–Я—Г—Б—В–Њ—В–∞¬ї (–ґ–µ–ї—В–∞—П –Р–ї—Б–Є–≥–љ–∞). вАУ –Ь.: –£–†–°–°, 2007, –°. 308, www.alsignat.narod.ru.
3. –У–∞—Г—Е–Љ–∞–љ –Ь.–•. –Р–ї–≥–µ–±—А–∞ —Б–Є–≥–љ–∞—В—Г—А ¬Ђ–І–∞—Б—В–Є—Ж—Л¬ї (–Ј–µ–ї–µ–љ–љ–∞—П –Р–ї—Б–Є–≥–љ–∞). вАУ –Ь.: –Ы–Є–±—А–Њ–Ї–Њ–Љ, 2008, –°. 422, www.alsignat.narod.ru.
4. –У–∞—Г—Е–Љ–∞–љ –Ь.–•. –Р–ї–≥–µ–±—А–∞ —Б–Є–≥–љ–∞—В—Г—А ¬Ђ–У—А–∞–≤–Є—В–∞—Ж–Є—П¬ї (–≥–Њ–ї—Г–±–∞—П –Р–ї—Б–Є–≥–љ–∞). вАУ –Ь.: –Ы–Є–±—А–Њ–Ї–Њ–Љ, 2009, –°. 294, www.alsignat.narod.ru.
5. –С–ї–Њ—Е–Є–љ—Ж–µ–≤ –Ф.–Ш. –Ю—Б–љ–Њ–≤—Л –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. вАУ –Ь.: –Т—Л—Б—И–∞—П —И–Ї–Њ–ї–∞, 1963, –°. 620.
6. –†—Л—В–Њ–≤ –°.–Ь. –Т–≤–µ–і–µ–љ–Є–µ –≤ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї—Г—О —А–∞–і–Є–Њ—Д–Є–Ј–Є–Ї—Г –І.1. вАУ –Ь.: –Э–∞—Г–Ї–∞, 1976, –°. 494.
7. –Ґ–Є—Е–∞–љ–Њ–≤ –Т.–Ш. –°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П —А–∞–і–Є–Њ—Д–Є–Ј–Є–Ї–∞. вАУ –Ь.: –†–∞–і–Є–Њ –Є —Б–≤—П–Ј—М, 1982, –°. 622.
8. –Т–µ–љ—В—Ж–µ–ї—М –Х.–°., –Ю–≤—З–∞—А–Њ–≤ –Ы.–Р. –Ґ–µ–Њ—А–Є—П —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –Є –µ–µ –Є–љ–ґ–µ–љ–µ—А–љ—Л–µ –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П. вАУ –Ь.: –Э–∞—Г–Ї–∞, 1991, –°. 383.
9. –Ы–∞–љ–і–∞—Г –Ы.–Ф., –Ы–Є—Д—И–Є—Ж –Х.–Ь. –Ъ–≤–∞–љ—В–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞. –Э–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–∞—П —В–µ–Њ—А–Є—П. вАУ –Ь.: –Э–∞—Г–Ї–∞, 1989, –°. 767.
10. –Я—А–Є–≥–Њ–ґ–Є–љ –Ш., –°—В–µ–љ–≥–µ—А—Б –Ш. –Я–Њ—А—П–і–Њ–Ї –Є–Ј —Е–∞–Њ—Б–∞. вАУ –Ь.: –≠–і–Є—В–Њ—А–Є–∞–ї –£–†–°–°, 2000, –°. 310.
11. –Я—А–Є–≥–Њ–ґ–Є–љ –Ш. –°—В–µ–љ–≥–µ—А—Б –Ш. –Т—А–µ–Љ—П, —Е–∞–Њ—Б, –Ї–≤–∞–љ—В. вАУ –Ь.: –≠–і–Є—В–Њ—А–Є–∞–ї –£–†–°–°, 2001, –°. 239.
12. –≠–ї—М—Б–≥–Њ–ї—М—Ж –Ы.–≠. –Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П –Є –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–µ –Є—Б—З–Є—Б–ї–µ–љ–Є–µ. вАУ –Ь.: –Э–∞—Г–Ї–∞, 1969, –°. 424.
13. –С–∞—В–∞–љ–Њ–≤ –Ь.–°. –Ъ–∞—З–µ—Б—В–≤–µ–љ–љ–Њ –љ–Њ–≤–Њ–µ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ —Б—В—А—Г–Ї—В—Г—А–љ–Њ–є –Њ—А–≥–∞–љ–Є–Ј–∞—Ж–Є–Є –Љ–∞—В–µ—А–Є–Є (–≤—Л–≤–Њ–і —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞). –Я—А–Њ–±–ї–µ–Љ—Л —В–µ—Е–љ–Є—З–µ—Б–Ї–Њ–є —Н–Ї—Б–њ–ї—Г–∞—В–∞—Ж–Є–Є –Є —Б–Њ–≤–µ—А—И–µ–љ—Б—В–≤–Њ–≤–∞–љ–Є—П –†–≠–Ю. –Ь–µ–ґ–≤—Г–Ј–Њ–≤—Б–Ї–Є–є —Б–±. –љ–∞—Г—З. —В—А. вАУ –Ь.: –†–Ш–Ю –Ь–Ш–Ш–У–Р, 1990, –°. 145 - 156.
14. –С–∞—В–∞–љ–Њ–≤ –Ь.–°. –Т–ї–Є—П–љ–Є–µ –њ–Њ–і—Б—В–Є–ї–∞—О—Й–µ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞ —В–Њ—З–љ–Њ—Б—В–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –Ї–≤–∞–Ј–Є–і–Њ–њ–ї–µ—А–Њ–≤—Б–Ї–Њ–≥–Њ –њ–µ–ї–µ–љ–≥–∞—В–Њ—А–∞. –Ф–Є—Б—Б–µ—А—В–∞—Ж–Є—П –Ї–∞–љ–і–Є–і–∞—В–∞ —В–µ—Е. –љ–∞—Г–Ї. вАУ –Ь.: –Ь–У–Ґ–£ –У–Р, 1994. –°. 214.
15. –°–∞–є—В www.alsignat.narod.ru.
CONCLUSION SCHR√ЦDINGER'S EQUATION FOR MICROSCOPIC AND MACROSCOPIC SYSTEMS
Batanov M.S., Cand.Tech.Sci., associate professor MAI, alsignat@yandex.ru
Abstract:
The based provisions of quantum mechanics (such as "matter
waves" of de Broil, "principle of uncertainty" of
Heisenberg, lack of the sizes and a trajectory of the movement at
elementary particles, and also emergence history Schr√ґdinger's
equation), are still not rather logical. Interest in sources of
quantum mechanics is caused still by that the advanced boundaries of
science in the field of studying of the structural organization of a
matter - the string theories which are based on quantum mechanics are
in difficulties almost irresistible (in my opinion). It forces to
return to reconsideration of fundamentals of quantum physics.
In underwritten article the model of chaotically wandering material particle (possessing the size and a trajectory of the movement) on the basis of which it was possible is offered:
- to remove Schr√ґdinger's equation;
- to attach to Planck's constant ƒІ concrete physical significance;
- to prove transition from coordinate representation statistical (including quantum-mechanical) systems to its pulse idea without attraction of idea of existence of "matter waves" of de Broil and "the principle of uncertainty" of Heisenberg.
Thus conditions and borders of application of the generalized Schr√ґdinger's equation to the description of the phenomena, both a microcosm, and macrocosm are revealed.
Besides, the intermediate result "determination of density of distribution of probability of a derivative of n-go of an order of n of times of differentiable, casual, stationary Markov process" can be applicable in many areas of statistical mechanics and radiophysics.
Keywords: Schr√ґdinger's equation, electron, density of distribution of probability of a derivative, particle, chaotic trajectory, coordinate representation.
LIST OF REFERENCES
1. Landau L.D., Lifshic E.M. Mehanika. вАУ M.: Nauka, 1988, S. 237.
2. Gauhman M.H. Algebra signatur ¬ЂPustota¬ї (zheltaja Alsigna). вАУ M.: URSS, 2007, S. 308, www.alsignat.narod.ru.
3. Gauhman M.H. Algebra signatur ¬ЂChasticy¬ї (zelennaja Alsigna). вАУ M.: Librokom, 2008, S. 422, www.alsignat.narod.ru.
4. Gauhman M.H. Algebra signatur ¬ЂGravitacija¬ї (golubaja Alsigna). вАУ M.: Lib-rokom, 2009, S. 294, www.alsignat.narod.ru.
5. Blohincev D.I. Osnovy kvantovoj mehaniki. вАУ M.: Vysshaja shkola, 1963, S. 620.
6. Rytov S.M. Vvedenie v statisticheskuju radiofiziku Ch.1. вАУ M.: Nauka, 1976,S. 494.
7. Tihanov V.I. Statisticheskaja radiofizika. вАУ M.: Radio i svjaz', 1982, S. 622.
8. Ventcel' E.S., Ovcharov L.A. Teorija sluchajnyh processov i ee inzhenernye prilozhenija. вАУ M.: Nauka, 1991, S. 383.
9. Landau L.D., Lifshic E.M. Kvantovaja mehanika. Nereljativistskaja teorija. вАУ M.: Nauka, 1989, S. 767.
10. Prigozhin I., Stengers I. Porjadok iz haosa. вАУ M.: Jeditorial URSS, 2000, S. 310.
11. Prigozhin I. Stengers I. Vremja, haos, kvant. вАУ M.: Jeditorial URSS, 2001, S. 239.
12. Jel'sgol'c L.Je. Differencial'nye uravnenija i variacionnoe ischislenie. вАУ M.: Nauka, 1969, S. 424.
13. Batanov M.S. Kachestvenno novoe ponimanie strukturnoj organizacii mate-rii (vyvod uravnenija Shredingera). Problemy tehnicheskoj jekspluatacii i sovershenstvovanija RJeO. Mezhvuzovskij sb. nauch. tr. вАУ M.: RIO MIIGA, 1990, S. 145 - 156.
14. Batanov M.S. Vlijanie podstilajushhej poverhnosti na tochnostnye harakte-ristiki kvazidoplerovskogo pelengatora. Dissertacija kandidata teh. nauk. вАУ M.: MGTU GA, 1994. S. 214.









