–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ґ–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–є –њ–Њ–і—Е–Њ–і –≤ –Ї–Њ—Б–Љ–Њ–ї–Њ–≥–Є–Є
–†—Г–±—А–Є–Ї–∞: –§–Є–Ј–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ1 2019» (—П–љ–≤–∞—А—М, 2019)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 1964
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ґ–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–є –њ–Њ–і—Е–Њ–і –≤ –Ї–Њ—Б–Љ–Њ–ї–Њ–≥–Є–Є
–Ш—Е–ї–Њ–≤ –С. –Ы.
Ikhlov B. L.
–Т–≤–µ–і–µ–љ–Є–µ
–Э–∞–њ—А—П–Љ—Г—О —Б–Њ–µ–і–Є–љ–Є—В—М —В–µ–Њ—А–Є—О —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤, —В–µ–Њ—А–Є—О –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –Є —А–µ–ї—П—В–Є–≤–Є–Ј–Љ –Ј–∞—В—А—Г–і–љ–Є—В–µ–ї—М–љ–Њ, –µ—Б—В–µ—Б—В–≤–µ–љ–љ—Л–Љ —Б–Њ–µ–і–Є–љ—П—О—Й–Є–Љ –Ј–≤–µ–љ–Њ–Љ —П–≤–ї—П–µ—В—Б—П —Б–≤–Њ–µ–≥–Њ —А–Њ–і–∞ ¬Ђ—В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–є –і–Є—Б–Ї—Г—А—Б¬ї.
–Э–∞ —Б–µ–≥–Њ–і–љ—П—И–љ–Є–є –Љ–Њ–Љ–µ–љ—В –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј—А–∞–±–Њ—В–∞–љ–∞ —В–µ–Њ—А–Є—П –≥–Њ—А—П—З–µ–є –Т—Б–µ–ї–µ–љ–љ–Њ–є, –≥–і–µ –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ–µ –Љ–µ—Б—В–Њ –Ј–∞–љ–Є–Љ–∞—О—В —Д–Є–Ј–Є—З–µ—Б–Ї–∞—П –Ї–Є–љ–µ—В–Є–Ї–∞, —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–є –Є —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є–є –њ–Њ–і—Е–Њ–і —Б —Д—Г–љ–Ї—Ж–Є—П–Љ–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П, —Г—А–∞–≤–љ–µ–љ–Є—П–Љ–Є —Б–Њ—Б—В–Њ—П–љ–Є—П –≤–µ—Й–µ—Б—В–≤–∞ –Є —В.–і.
–Ю–і–љ–∞–Ї–Њ –≤ —В–µ–Љ–µ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –≤ —В–µ–Њ—А–Є–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Є –Є, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –≤ –Ї–Њ—Б–Љ–Њ–ї–Њ–≥–Є–Є, —Б—Г—Й–µ—Б—В–≤—Г—О—В –і–≤–µ –њ—А–Њ–±–ї–µ–Љ—Л: 1) –∞–і–µ–Ї–≤–∞—В–љ–Њ—Б—В—М —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –і–ї—П –Т—Б–µ–ї–µ–љ–љ–Њ–є –≤ —Ж–µ–ї–Њ–Љ, 2) —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞–љ–Є–µ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –≤ –Ї–Њ–≤–∞—А–Є–∞–љ—В–љ–Њ–Љ –≤–Є–і–µ –і–ї—П –ї–Њ–Ї–∞–ї—М–љ—Л—Е —Б–Є—Б—В–µ–Љ.
–Ґ–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ вАФ —Н—В–Њ —Б–Є—Б—В–µ–Љ–∞ –Љ–љ–Њ–≥–Є—Е —З–∞—Б—В–Є—Ж, –Ї–Њ—В–Њ—А—Л–µ –і–µ–ї—П—В—Б—П –љ–∞ –≥—А—Г–њ–њ—Л —В–Њ–ґ–і–µ—Б—В–≤–µ–љ–љ—Л—Е —З–∞—Б—В–Є—Ж (–∞—В–Њ–Љ–Њ–≤ –Є–ї–Є –Љ–Њ–ї–µ–Ї—Г–ї). –≠—В–Є —З–∞—Б—В–Є—Ж—Л –њ–Њ—Б—В–Њ—П–љ–љ–Њ —Б—В–∞–ї–Ї–Є–≤–∞—О—В—Б—П –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є, —З—В–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –≤–≤–µ—Б—В–Є –і–ї–Є–љ—Г —Б–≤–Њ–±–Њ–і–љ–Њ–≥–Њ –њ—А–Њ–±–µ–≥–∞ –Є —Б—А–µ–і–љ–Є–є –Ї–≤–∞–і—А–∞—В —Б–Ї–Њ—А–Њ—Б—В–Є. –Ґ–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ —В–≤–µ—А–і—Л—Е —В–µ–ї –±–∞–Ј–Є—А—Г–µ—В—Б—П –љ–∞ –љ–∞–ї–Є—З–Є–Є –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е —В–Є–њ–Њ–≤ —В–Њ–ґ–і–µ—Б—В–≤–µ–љ–љ—Л—Е –Љ–љ–Њ–≥–Є—Е —З–∞—Б—В–Є—Ж, –Ї–Њ–ї–µ–±–ї—О—Й–Є—Е—Б—П –Њ–Ї–Њ–ї–Њ –њ–Њ–ї–Њ–ґ–µ–љ–Є—П —А–∞–≤–љ–Њ–≤–µ—Б–Є—П. –Ґ–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –ґ–Є–і–Ї–Њ—Б—В–µ–є, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –њ–ї–∞–Ј–Љ—Л, –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–µ—В –љ–∞–ї–Є—З–Є–µ —В–∞–Ї–Є—Е —Б–≤—П–Ј–µ–є, –Ї–∞–Ї —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–µ–њ—А–µ—А—Л–≤–љ–Њ—Б—В–Є, —Г—А–∞–≤–љ–µ–љ–Є—П —В–µ–њ–ї–Њ–њ–µ—А–µ–љ–Њ—Б–∞ –Є —В.–і.
–Ф–ї—П —Б–Є—Б—В–µ–Љ—Л –Є–ї–Є –і–≤—Г—Е, —В–µ—Е, n —Б–Њ–њ—А–Є–Ї–∞—Б–∞—О—Й–Є—Е—Б—П —Б–Є—Б—В–µ–Љ –Љ–Њ–ґ–љ–Њ –≤–µ—Б—В–Є –њ–Њ–љ—П—В–Є—П —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, —В–µ—А–Љ–Њ—Б—В–∞—В–∞ –Є —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л.
–Т–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є –ґ–µ –љ–µ—В —Б—В–Њ–ї–Ї–љ–Њ–≤–µ–љ–Є–є –≤ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ. –Ю–і–љ–∞ —З–∞—Б—В—М –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ –Ј–∞–њ–Њ–ї–љ–µ–љ–∞ –≥–∞–ї–∞–Ї—В–Є–Ї–∞–Љ–Є, –Љ–∞—Б—Б—Л –Ї–Њ—В–Њ—А—Л—Е –Ї–Њ–ї–µ–±–ї—О—В—Б—П –Њ—В –њ–Њ—А—П–і–Ї–∞ 101 –і–Њ –њ–Њ—А—П–і–Ї–∞ 103 –Љ–ї—А–і. —Б–Њ–ї–љ–µ—З–љ—Л—Е –Љ–∞—Б—Б. –Т—Б–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Ј–≤–µ–Ј–і –≤ –≤–Є–і–Є–Љ–Њ–є —З–∞—Б—В–Є (–≤ –љ–∞—И–µ–є –≥–∞–ї–∞–Ї—В–Є–Ї–µ вАФ 1011 –Ј–≤–µ–Ј–і), –њ–Њ—А—П–і–Ї–∞ 1011 –≥–∞–ї–∞–Ї—В–Є–Ї. –У–∞–ї–∞–Ї—В–Є–Ї–Є —Б—Ж–µ–њ–ї—П—О—В—Б—П –≤ —Б–Ї–Њ–њ–ї–µ–љ–Є—П, 90% –≥–∞–ї–∞–Ї—В–Є–Ї вАФ –≤ —Б–Ї–Њ–њ–ї–µ–љ–Є—П—Е.
–Ш–Ј –љ–Є—Е 107 вАФ —Б–≤–µ—А—Е—Б–Ї–Њ–њ–ї–µ–љ–Є—П –Є–Ј —В—Л—Б—П—З –≥–∞–ї–∞–Ї—В–Є–Ї, вАФ –≥–∞–ї–∞–Ї—В–Є—З–µ—Б–Ї–Є–µ –≥—А—Г–њ–њ—Л, вАФ –≥–Є–≥–∞–љ—В—Б–Ї–Є–µ –≥–∞–ї–∞–Ї—В–Є–Ї–Є, вАФ –Ї–∞—А–ї–Є–Ї–Њ–≤—Л–µ –≥–∞–ї–∞–Ї—В–Є–Ї–Є, –Є —Н—В–Њ –ї–Є—И—М –Љ–∞–ї–∞—П —З–∞—Б—В—М, —В.–Ї. 9/10 –≥–∞–ї–∞–Ї—В–Є–Ї –Њ—В –љ–∞—Б —Б–Ї—А—Л—В–Њ.
–°–≤–µ—А—Е—Б–Ї–Њ–њ–ї–µ–љ–Є—П –Њ–±—А–∞–Ј—Г—О—В —Ж–µ–њ–Њ—З–Ї–Є, –љ–∞–њ—А–Є–Љ–µ—А, —Ж–µ–њ–Њ—З–Ї–∞ –Ь–∞—А–Ї–∞—А—П–љ–∞.
–Ф—А—Г–≥–Є–µ —З–∞—Б—В–Є –Т—Б–µ–ї–µ–љ–љ–Њ–є, –≤–Њ–є–і—Л, —А–∞–Ј–Љ–µ—А–Њ–Љ –≤ —Б–Њ—В–љ–Є –Ь–њ–Ї вАФ –њ—Г—Б—В—Л. –¶–µ–њ–Њ—З–Ї–Є –Є –≤–Њ–є–і—Л –Є–љ–Њ–≥–і–∞ –Њ–±—А–∞–Ј—Г—О—В —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ—Л–µ —Б—В–µ–љ—Л, –љ–∞–њ—А–Є–Љ–µ—А, –Т–µ–ї–Є–Ї–∞—П —Б—В–µ–љ–∞ –°–ї–Њ—Г–љ–∞. –Т–µ–ї–Є–Ї–∞—П —Б—В–µ–љ–∞ CfA2, –љ–∞—Е–Њ–і—П—Й–∞—П—Б—П –Њ—В –љ–∞—Б –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 200 –Љ–ї–љ —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В, –Є–Љ–µ–µ—В —В–Њ–ї—Й–Є–љ—Г 15 –Љ–ї–љ —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В –Є –њ—А–Њ—В—П–ґ–µ–љ–љ–Њ—Б—В—М –њ–Њ—А—П–і–Ї–∞ 500 –Љ–ї–љ —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В. –°—В–µ–љ–∞ ¬Ђ–У—А–Њ–Љ–∞–і–љ–∞—П –≥—А—Г–њ–њ–∞ –Ї–≤–∞–Ј–∞—А–Њ–≤¬ї –Є–Љ–µ–µ—В —А–∞–Ј–Љ–µ—А 4 –Љ–ї—А–і. —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В, –Т–µ–ї–Є–Ї–∞—П —Б—В–µ–љ–∞ –У–µ—А–Ї—Г–ї–µ—Б вАФ –°–µ–≤–µ—А–љ–∞—П –Ї–Њ—А–Њ–љ–∞ вАФ 10 –Љ–ї—А–і. —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В.
–Э–∞–Ї–Њ–љ–µ—Ж, –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—О—В —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ –µ—Й–µ –љ–µ –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ–Њ–≥–Њ –Т–µ–ї–Є–Ї–Њ–≥–Њ –Р—В—В—А–∞–Ї—В–Њ—А–∞, –Ї–ї–∞—Б—В–µ—А–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ —Б–≤–µ—А—Е—Б–Ї–Њ–њ–ї–µ–љ–Є–є, –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–µ–≥–Њ –≤–µ—Й–µ—Б—В–≤–Њ –љ–∞—И–µ–≥–Њ —Б–µ–Ї—В–Њ—А–∞ –Т—Б–µ–ї–µ–љ–љ–Њ–є.
–І–∞—Б—В—М –Т—Б–µ–ї–µ–љ–љ–Њ–є вАФ –±–∞—А–Є–Њ–љ–љ–∞—П –Љ–∞—В–µ—А–Є—П, 5%, —З–∞—Б—В—М вАФ —В–µ–Љ–љ–∞—П —Н–љ–µ—А–≥–Є—П, 75%, —З–∞—Б—В—М вАФ —В–µ–Љ–љ–∞—П –Љ–∞—В–µ—А–Є—П, 20%. –Т—Б–µ–ї–µ–љ–љ–∞—П –Ј–∞–њ–Њ–ї–љ–µ–љ–∞ –њ—А–Њ—В–Њ–љ–∞–Љ–Є, —Н–ї–µ–Ї—В—А–Њ–љ–∞–Љ–Є, –≤–Њ–і–Њ—А–Њ–і–Њ–Љ, –≥–µ–ї–Є–µ–Љ, —А–µ–ї–Є–Ї—В–Њ–≤—Л–Љ –Є–Ј–ї—Г—З–µ–љ–Є–µ–Љ, –Є–Ј–ї—Г—З–µ–љ–Є–µ–Љ –Ј–≤–µ–Ј–і, –∞—Б—В–µ—А–Њ–Є–і–∞–Љ–Є. 60% –±–∞—А–Є–Њ–љ–љ–Њ–є –Љ–∞—В–µ—А–Є–Є вАФ –≤ –Љ–µ–ґ–≥–∞–ї–∞–Ї—В–Є—З–µ—Б–Ї–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ, –љ–µ–і–∞–≤–љ–Њ —В–∞–Љ –Њ–±–љ–∞—А—Г–ґ–µ–љ—Л –љ–Є—В–Є –њ–ї–Њ—В–љ–Њ–≥–Њ –≥–∞–Ј–∞ –Є–Ј –≤—Л—Б–Њ–Ї–Њ –Є–Њ–љ–Є–Ј–Є—А–Њ–≤–∞–љ–љ—Л—Е –∞—В–Њ–Љ–Њ–≤ –Ї–Є—Б–ї–Њ—А–Њ–і–∞ –њ—А–Є —В–µ–Љ–њ–µ—А–∞—В—Г—А–µ 60 –Љ–ї–љ –≥—А–∞–і—Г—Б–Њ–≤, –Ї–Њ—В–Њ—А—Л–µ —Б–Њ—Б—В–∞–≤–ї—П—О—В 30% –≤—Б–µ–є –±–∞—А–Є–Њ–љ–љ–Њ–є –Љ–∞—В–µ—А–Є–Є [1].
–Э–µ–і–∞–≤–љ–Њ –Њ–±–љ–∞—А—Г–ґ–Є–ї–Њ—Б—М, —З—В–Њ —З–Є—Б–ї–Њ –≥–∞–ї–∞–Ї—В–Є–Ї —А–∞–љ–µ–µ –љ–µ–і–Њ–Њ—Ж–µ–љ–Є–≤–∞–ї–Є –≤
–Я—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ –≤ –Љ–∞—Б—И—В–∞–±–∞—Е –њ–Њ—А—П–і–Ї–∞ 300 –Ь–њ–Ї –Т—Б–µ–ї–µ–љ–љ–∞—П –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –Њ–і–љ–Њ—А–Њ–і–љ–∞ –Є –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В—М –љ–Є—В–µ–≤–Є–і–љ—Л—Е —Б–Ї–Њ–њ–ї–µ–љ–Є–є –≥–∞–ї–∞–Ї—В–Є–Ї, –Љ–µ–ґ–і—Г –Ї–Њ—В–Њ—А—Л–Љ–Є вАФ –≤–Њ–є–і—Л.
–Ґ–Њ –µ—Б—В—М, –њ–Њ —Б–≤–Њ–µ–є –Ї–Њ–љ—Б–Є—Б—В–µ–љ—Ж–Є–Є –Т—Б–µ–ї–µ–љ–љ–∞—П –љ–µ —П–≤–ї—П–µ—В—Б—П —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–Њ–є. –Т—Б–µ–ї–µ–љ–љ–∞—П –љ–∞–њ–Њ–Љ–Є–љ–∞–µ—В –±–Є–Њ–Љ–∞—Б—Б—Г –Њ–Ї–µ–∞–љ–∞, –≥–і–µ –Љ–Є–Ї—А–Њ–Њ—А–≥–∞–љ–Є–Ј–Љ—Л вАФ –Љ–µ–ґ–Ј–≤–µ–Ј–і–љ—Л–є –≥–∞–Ј, –∞—В–Њ–ї–ї—Л вАФ –Ј–≤–µ–Ј–і–љ—Л–µ —Б–Ї–Њ–њ–ї–µ–љ–Є—П, –љ–Њ –±–µ–Ј –≤–Њ–і—Л.
–Т–љ—Г—В—А–Є —Б–µ–±—П –У–∞–ї–∞–Ї—В–Є–Ї–Є вАФ –±–µ—Б—Б—В–Њ–ї–Ї–љ–Њ–≤–Є—В–µ–ї—М–љ—Л. –Ґ–Њ –µ—Б—В—М, –≥–Њ–≤–Њ—А–Є—В—М –і–∞–ґ–µ –Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–µ –≤–љ—Г—В—А–Є –≥–∞–ї–∞–Ї—В–Є–Ї вАФ –Ј–∞—В—А—Г–і–љ–Є—В–µ–ї—М–љ–Њ. –І–∞—Й–µ —Б–Њ—Г–і–∞—А—П—О—В—Б—П —Б–∞–Љ–Є –≥–∞–ї–∞–Ї—В–Є–Ї–Є. –Х—Б–ї–Є –Є—Б—Е–Њ–і–Є—В—М –Є–Ј —З–∞—Б—В–Њ—В—Л —Б–Њ—Г–і–∞—А–µ–љ–Є–є –Љ–Њ–ї–µ–Ї—Г–ї –≤ –≥–∞–Ј–µ, —З–∞—Б—В–Њ—В–∞ —Б–Њ—Г–і–∞—А–µ–љ–Є–є –≥–∞–ї–∞–Ї—В–Є–Ї –њ–Њ—А—П–і–Ї–∞ 10-14 –≤ –≥–Њ–і, —А–µ–∞–ї—М–љ–Њ вАФ –љ–∞ –і–≤–∞ –њ–Њ—А—П–і–Ї–µ –Љ–µ–љ—М—И–µ. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —Б—В–Њ–ї–Ї–љ–Њ–≤–µ–љ–Є—П –≥–∞–ї–∞–Ї—В–Є–Ї –љ–µ –љ–Њ—Б—П—В —Е–∞—А–∞–Ї—В–µ—А —Б–Њ—Г–і–∞—А–µ–љ–Є–є –Љ–µ–ґ–і—Г –Љ–Њ–ї–µ–Ї—Г–ї–∞–Љ–Є, –≤ —Б–ї—Г—З–∞–µ –Є—Е —Б–ї–Є—П–љ–Є—П (–Љ–µ—А–ґ–Є–љ–≥–∞) –≤ –љ–Є—Е –∞–Ї—В–Є–≤–Є–Ј–Є—А—Г–µ—В—Б—П –њ—А–Њ—Ж–µ—Б—Б –Ј–≤–µ–Ј–і–Њ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –≥–∞–ї–∞–Ї—В–Є–Ї вАФ –њ–Њ–і –≤–Њ–њ—А–Њ—Б–Њ–Љ.
–Т–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є –љ–µ—В –ї–Њ–Ї–∞–ї—М–љ–Њ–≥–Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤–≤–µ—Б—В–Є –њ–Њ–љ—П—В–Є—П —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –≤ —Ж–µ–ї–Њ–Љ, —В–µ—А–Љ–Њ—Б—В–∞—В–∞ –≤ —Ж–µ–ї–Њ–Љ, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л. –Ь–Њ–ґ–љ–Њ –≥–Њ–≤–Њ—А–Є—В—М –ї–Є—И—М –Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–µ —Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤, —Б–њ–µ–Ї—В—А –Є—Е —Н–љ–µ—А–≥–Є–є –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ –Ь–∞–Ї—Б–≤–µ–ї–ї–∞, –Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–µ —А–µ–ї–Є–Ї—В–Њ–≤–Њ–≥–Њ –Є–Ј–ї—Г—З–µ–љ–Є—П (—Г—А–∞–≤–љ–µ–љ–Є–µ –°—В–µ—Д–∞–љ–∞-–С–Њ–ї—М—Ж–Љ–∞–љ–∞), –Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–µ –Њ–±–ї–∞–Ї–Њ–≤ –≥–∞–Ј–∞, –і–ї—П –Ї–Њ—В–Њ—А—Л—Е –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М
–Я—А–Є–≤–µ–і–µ–Љ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ: –≤–µ—З–љ—Л–є –і–≤–Є–≥–∞—В–µ–ї—М –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ вАФ –љ–µ–Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ –і–Њ–ї–≥–Њ –і–µ–є—Б—В–≤—Г—О—Й–∞—П –Љ–∞—И–Є–љ–∞, –Ї–Њ—В–Њ—А–∞—П, –±—Г–і—Г—З–Є –њ—Г—Й–µ–љ–∞ –≤ —Е–Њ–і, –њ—А–µ–≤—А–∞—Й–∞–ї–∞ –±—Л –≤ —А–∞–±–Њ—В—Г –≤—Б—С —В–µ–њ–ї–Њ, –Є–Ј–≤–ї–µ–Ї–∞–µ–Љ–Њ–µ –Є–Ј –Њ–Ї—А—Г–ґ–∞—О—Й–Є—Е —В–µ–ї. –Э–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Њ—Б—Г—Й–µ—Б—В–≤–ї–µ–љ–Є—П –≤–µ—З–љ–Њ–≥–Њ –і–≤–Є–≥–∞—В–µ–ї—П –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ –њ–Њ—Б—В—Г–ї–Є—А—Г–µ—В—Б—П –≤ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–µ –≤ –Ї–∞—З–µ—Б—В–≤–µ –Њ–і–љ–Њ–є –Є–Ј —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Л—Е —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Њ–Ї –≤—В–Њ—А–Њ–≥–Њ –љ–∞—З–∞–ї–∞ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є: –≤–Њ –≤—Б–µ—Е –љ–µ–Њ–±—А–∞—В–Є–Љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–∞—Е —Н–љ—В—А–Њ–њ–Є—П –Є–Ј–Њ–ї–Є—А–Њ–≤–∞–љ–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В: 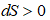 .
.
–Т—Б–µ–ї–µ–љ–љ–∞—П, —П–≤–ї—П—П—Б—М –Є–Ј–Њ–ї–Є—А–Њ–≤–∞–љ–љ–Њ–є —Б–Є—Б—В–µ–Љ–Њ–є, –љ–µ –Њ–±–Љ–µ–љ–Є–≤–∞–µ—В—Б—П —В–µ–њ–ї–Њ–Љ, –њ–Њ—Н—В–Њ–Љ—Г 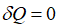 , —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, 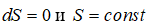 . –Р–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Є–є –њ—А–Њ—Ж–µ—Б—Б, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ S = const, –Њ–±—А–∞—В–Є–Љ. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –≤ –Њ—В–ї–Є—З–Є–µ –Њ—В —А–∞—Б—И–Є—А–µ–љ–Є—П –≥–∞–Ј–∞ –≤ –њ—Г—Б—В–Њ—В—Г, –≤ —Б–ї—Г—З–∞–µ —А–∞—Б—И–Є—А–µ–љ–Є—П –Т—Б–µ–ї–µ–љ–љ–Њ–є –њ—Г—Б—В–Њ—В–∞ –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В, –Т—Б–µ–ї–µ–љ–љ–∞—П –µ—Й–µ –і–Њ–ї–ґ–љ–∞ –Ї–∞–ґ–і—Л–є –Љ–Њ–Љ–µ–љ—В —А–∞—Б—И–Є—А–µ–љ–Є—П –њ–Њ—А–Њ–ґ–і–∞—В—М –њ—Г—Б—В–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –≤–Њ–Ї—А—Г–≥ —Б–µ–±—П. –І—В–Њ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Њ –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є –≤–µ—З–љ–Њ–≥–Њ –і–≤–Є–≥–∞—В–µ–ї—П
. –Р–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Є–є –њ—А–Њ—Ж–µ—Б—Б, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ S = const, –Њ–±—А–∞—В–Є–Љ. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –≤ –Њ—В–ї–Є—З–Є–µ –Њ—В —А–∞—Б—И–Є—А–µ–љ–Є—П –≥–∞–Ј–∞ –≤ –њ—Г—Б—В–Њ—В—Г, –≤ —Б–ї—Г—З–∞–µ —А–∞—Б—И–Є—А–µ–љ–Є—П –Т—Б–µ–ї–µ–љ–љ–Њ–є –њ—Г—Б—В–Њ—В–∞ –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В, –Т—Б–µ–ї–µ–љ–љ–∞—П –µ—Й–µ –і–Њ–ї–ґ–љ–∞ –Ї–∞–ґ–і—Л–є –Љ–Њ–Љ–µ–љ—В —А–∞—Б—И–Є—А–µ–љ–Є—П –њ–Њ—А–Њ–ґ–і–∞—В—М –њ—Г—Б—В–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –≤–Њ–Ї—А—Г–≥ —Б–µ–±—П. –І—В–Њ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Њ –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є –≤–µ—З–љ–Њ–≥–Њ –і–≤–Є–≥–∞—В–µ–ї—П 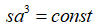 , –≥–і–µ s вАФ –њ–ї–Њ—В–љ–Њ—Б—В—М —Н–љ—В—А–Њ–њ–Є–Є, –Ї–Њ—В–Њ—А–∞—П –њ–∞–і–∞–µ—В —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ —А–∞–і–Є—Г—Б–∞ a. –І—В–Њ –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ—В –≤—Л–≤–Њ–і –Њ —Б–Њ—Е—А–∞–љ–µ–љ–Є–Є —Н–љ—В—А–Њ–њ–Є–Є –≤ –Њ–±—К–µ–Љ–µ –≤—Б–µ–є –Т—Б–µ–ї–µ–љ–љ–Њ–є. –≠—В–Њ, –Ї–∞–Ј–∞–ї–Њ—Б—М –±—Л, –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ—В —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В—М –њ—А–µ–і—Л–і—Г—Й–µ–≥–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П. –Ю–і–љ–∞–Ї–Њ –≤ [2] —Г–Ї–∞–Ј—Л–≤–∞—О—В, —З—В–Њ —Н—В–Њ –Ї–Њ–≤–∞—А–Є–∞–љ—В–љ—Л–є –Ј–∞–Ї–Њ–љ. –Э–Њ –і–µ–ї–Њ –≤ —В–Њ–Љ, —З—В–Њ S —П–≤–ї—П–µ—В—Б—П –∞–і–і–Є—В–Є–≤–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–Њ–є, –њ–Њ—Н—В–Њ–Љ—Г –і–∞–љ–љ–Њ–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ –і–ї—П –ї—О–±—Л—Е —А–∞—Б—И–Є—А—П—О—Й–Є—Е—Б—П –Є–Ј–Њ–ї–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б–Є—Б—В–µ–Љ.)
, –≥–і–µ s вАФ –њ–ї–Њ—В–љ–Њ—Б—В—М —Н–љ—В—А–Њ–њ–Є–Є, –Ї–Њ—В–Њ—А–∞—П –њ–∞–і–∞–µ—В —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ —А–∞–і–Є—Г—Б–∞ a. –І—В–Њ –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ—В –≤—Л–≤–Њ–і –Њ —Б–Њ—Е—А–∞–љ–µ–љ–Є–Є —Н–љ—В—А–Њ–њ–Є–Є –≤ –Њ–±—К–µ–Љ–µ –≤—Б–µ–є –Т—Б–µ–ї–µ–љ–љ–Њ–є. –≠—В–Њ, –Ї–∞–Ј–∞–ї–Њ—Б—М –±—Л, –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ—В —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В—М –њ—А–µ–і—Л–і—Г—Й–µ–≥–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П. –Ю–і–љ–∞–Ї–Њ –≤ [2] —Г–Ї–∞–Ј—Л–≤–∞—О—В, —З—В–Њ —Н—В–Њ –Ї–Њ–≤–∞—А–Є–∞–љ—В–љ—Л–є –Ј–∞–Ї–Њ–љ. –Э–Њ –і–µ–ї–Њ –≤ —В–Њ–Љ, —З—В–Њ S —П–≤–ї—П–µ—В—Б—П –∞–і–і–Є—В–Є–≤–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–Њ–є, –њ–Њ—Н—В–Њ–Љ—Г –і–∞–љ–љ–Њ–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ –і–ї—П –ї—О–±—Л—Е —А–∞—Б—И–Є—А—П—О—Й–Є—Е—Б—П –Є–Ј–Њ–ї–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б–Є—Б—В–µ–Љ.)
–Т–≤–µ–і–µ–љ–Є–µ —В–Њ–ї—М–Ї–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–≥–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П –љ–∞—А—Г—И–∞–µ—В
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П
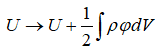 ,
,
–У–і–µ 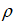 вАФ –њ–ї–Њ—В–љ–Њ—Б—В—М,
вАФ –њ–ї–Њ—В–љ–Њ—Б—В—М, 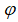 вАФ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤–љ–µ—И–љ–µ–≥–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П. –Ґ–Њ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤–Є–і–Њ–Є–Ј–Љ–µ–љ–µ–љ–љ—Л–є
вАФ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤–љ–µ—И–љ–µ–≥–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П. –Ґ–Њ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤–Є–і–Њ–Є–Ј–Љ–µ–љ–µ–љ–љ—Л–є
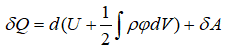
–Ю–і–љ–∞–Ї–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Е–∞–±–±–ї–Њ–≤—Б–Ї–Њ–µ —А–∞—Б—И–Є—А–µ–љ–Є–µ —Б–Њ–≤–µ—А—И–∞–µ—В —А–∞–±–Њ—В—Г –њ—А–Њ—В–Є–≤ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л—Е —Б–Є–ї, –Є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤–љ–µ—И–љ–Є–µ –Є—Б—В–Њ—З–љ–Є–Ї–Є —А–∞—Б—И–Є—А–µ–љ–Є—П –Њ—В—Б—Г—В—Б—В–≤—Г—О—В, –Т—Б–µ–ї–µ–љ–љ–∞—П –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є –≤–µ—З–љ—Л–є –і–≤–Є–≥–∞—В–µ–ї—М
–Т —Б—В—А—Г–љ–љ–Њ–є –Ь-—В–µ–Њ—А–Є–Є, –≤ –Љ–Њ–і–µ–ї–Є –њ—Г–ї—М—Б–Є—А—Г—О—Й–µ–є –Т—Б–µ–ї–µ–љ–љ–Њ–є –Є –≤ –Љ–Њ–і–µ–ї–Є –Ы–Є–љ–і–µ-–°—В–∞—А–Њ–±–Є–љ—Б–Ї–Њ–≥–Њ –Т—Б–µ–ї–µ–љ–љ–∞—П вАФ —В–Њ–ґ–µ –≤–µ—З–љ—Л–є –і–≤–Є–≥–∞—В–µ–ї—М.
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –Ї–∞–Ї –Љ–љ–Њ–≥–Њ–Ї—А–∞—В–љ–Њ –Њ—В–Љ–µ—З–∞–ї–Њ—Б—М –≤ –ї–Є—В–µ—А–∞—В—Г—А–µ, –µ—Б–ї–Є –≥–Њ–≤–Њ—А–Є—В—М –Њ —Б–Є–љ–≥—Г–ї—П—А–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є –≤ –Љ–Њ–Љ–µ–љ—В —А–Њ–ґ–і–µ–љ–Є—П –Т—Б–µ–ї–µ–љ–љ–Њ–є, —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –Є –њ–ї–Њ—В–љ–Њ—Б—В—М –љ–µ –Љ–Њ–≥—Г—В –±—Л—В—М –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –±–µ—Б–Ї–Њ–љ–µ—З–љ—Л–Љ–Є, —В.–Ї. –њ—А–Є –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–є –њ–ї–Њ—В–љ–Њ—Б—В–Є —Н–љ—В—А–Њ–њ–Є—П —Б—В—А–µ–Љ–Є—В—Б—П –Ї –љ—Г–ї—О, —З–µ–≥–Њ –њ—А–Є –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–є —В–µ–Љ–њ–µ—А–∞—В—Г—А–µ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М. –Э–Њ –Є –≤ –њ–ї–∞–љ–Ї–Њ–≤—Б–Ї–Њ–Љ –Љ–∞—Б—И—В–∞–±–µ –њ—А–Є –≤—Л—Б–Њ–Ї–Њ–є —В–µ–Љ–њ–µ—А–∞—В—Г—А–µ —Н–љ—В—А–Њ–њ–Є—П вАФ –Є—Б—З–µ–Ј–∞—О—Й–µ –Љ–∞–ї–∞—П –≤–µ–ї–Є—З–Є–љ–∞.
–Э–∞ –њ–ї–∞–љ–Ї–Њ–≤—Б–Ї–Њ–Љ –Љ–∞—Б—И—В–∞–± –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ-–≤—А–µ–Љ—П –љ–µ —П–≤–ї—П–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л–Љ, –њ–Њ–Ј–≤–Њ–ї–Є—В—М –њ—А–Њ—Ж–µ–і—Г—А—Г —Г—Б—А–µ–і–љ–µ–љ–Є—П, –њ–Њ—Н—В–Њ–Љ—Г, –Ї–∞–Ј–∞–ї–Њ—Б—М –±—Л, –≤–≤–µ—Б—В–Є —В–µ–Љ–њ–µ—А–∞—В—Г—А—Г –љ–µ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В—Б—П –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–Љ. –Э–Њ, —Е–Њ—В—П –≤ —Д–∞–Ј–µ –Т–µ–ї–Є–Ї–Њ–≥–Њ –Њ–±—К–µ–і–Є–љ–µ–љ–Є—П —Б–њ–Њ–љ—В–∞–љ–љ–Њ–≥–Њ –љ–∞—А—Г—И–µ–љ–Є—П –Њ–±—Й–µ–є –Ї–∞–ї–Є–±—А–Њ–≤–Њ—З–љ–Њ–є –≥—А—Г–њ–њ—Л –і–Њ —Н–ї–µ–Ї—В—А–Њ–Љ–∞–≥–љ–Є—В–љ–Њ–≥–Њ U(1)-—Б–µ–Ї—В–Њ—А–∞ –µ—Й–µ –љ–µ –њ—А–Њ–Є–Ј–Њ—И–ї–Њ, –Є–Ј–ї—Г—З–µ–љ–Є–µ –≤–Њ–Ј–љ–Є–Ї–∞–µ—В —Г–ґ–µ –≤ –љ–∞—З–∞–ї–µ –њ–ї–∞–љ–Ї–Њ–≤—Б–Ї–Њ–є —Н–њ–Њ—Е–Є, —З—В–Њ –Є –њ–Њ–Ј–≤–Њ–ї—П–µ—В –≥–Њ–≤–Њ—А–Є—В—М –Њ –њ–ї–∞–љ–Ї–Њ–≤—Б–Ї–Њ–є —В–µ–Љ–њ–µ—А–∞—В—Г—А–µ –Ї–∞–Ї –љ–µ–Ї–Њ–є –њ—А–µ–і–µ–ї—М–љ–Њ–є.
–Х—Й–µ –Њ–і–љ–Њ –Ј–∞—В—А—Г–і–љ–µ–љ–Є–µ –≤ —В–Њ–Љ, —З—В–Њ
–°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Н–љ—В—А–Њ–њ–Є–Є –≤ —Д–Њ—А–Љ–µ –®–µ–љ–љ–Њ–љ–∞ —В–Њ–ґ–µ –њ—А–Є–ї–Њ–ґ–Є–Љ–Њ –≤ —В–µ–Њ—А–Є–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Є –ї–Є—И—М –ї–Њ–Ї–∞–ї—М–љ–Њ.
–Э–∞–Ї–Њ–љ–µ—Ж, –≤ –Њ–±—Й–µ–є —В–µ–Њ—А–Є–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є (–Ю–Ґ–Ю) –љ–µ—В –њ–Њ–љ—П—В–Є–є —В–µ—А–Љ–Њ—Б—В–∞—В–∞ –Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П.
–Ь–µ–ґ–Ј–≤–µ–Ј–і–љ–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ
–Т –Љ–µ–ґ–њ–ї–∞–љ–µ—В–љ–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —Б–Њ–і–µ—А–ґ–Є—В—Б—П –Њ–Ї–Њ–ї–Њ 10 –Љ–Њ–ї–µ–Ї—Г–ї –≤–Њ–і–Њ—А–Њ–і–∞ –Є –≥–µ–ї–Є—П –љ–∞ 1 —Б–Љ3; –≤ –Љ–µ–ґ–Ј–≤–µ–Ј–і–љ–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —Б–Њ–і–µ—А–ґ–Є—В—Б—П –Њ–Ї–Њ–ї–Њ 1 –Љ–Њ–ї–µ–Ї—Г–ї—Л –≤ 1 —Б–Љ3; –≤ –Љ–µ–ґ–≥–∞–ї–∞–Ї—В–Є—З–µ—Б–Ї–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —Б–Њ–і–µ—А–ґ–Є—В—Б—П 10-6 –Љ–Њ–ї–µ–Ї—Г–ї –≤ 1 —Б–Љ3. –Я–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤—Г —З–∞—Б—В–Є—Ж —Б –љ–µ–љ—Г–ї–µ–≤–Њ–є –Љ–∞—Б—Б–Њ–є –њ–Њ–Ї–Њ—П –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Є–µ –ї—Г—З–Є –љ–∞ 92% —Б–Њ—Б—В–Њ—П—В –Є–Ј –њ—А–Њ—В–Њ–љ–Њ–≤, –љ–∞ 6% вАФ –Є–Ј —П–і–µ—А –≥–µ–ї–Є—П, –Њ–Ї–Њ–ї–Њ 1% —Б–Њ—Б—В–∞–≤–ї—П—О—В –±–Њ–ї–µ–µ —В—П–ґ–µ–ї—Л–µ —Н–ї–µ–Љ–µ–љ—В—Л, –Є –Њ–Ї–Њ–ї–Њ 1% –њ—А–Є—Е–Њ–і–Є—В—Б—П –љ–∞ —Н–ї–µ–Ї—В—А–Њ–љ—Л.
–Я–ї–Њ—В–љ–Њ—Б—В—М —Н–љ–µ—А–≥–Є–Є —А–µ–ї–Є–Ї—В–Њ–≤–Њ–≥–Њ –Є–Ј–ї—Г—З–µ–љ–Є—П —Б–Њ—Б—В–∞–≤–ї—П–µ—В 0,25 —Н–Т/—Б–Љ3 (4¬Ј10вИТ14 –Ф–ґ/–Љ3) –Є–ї–Є
–≠–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Є–є —Б–њ–µ–Ї—В—А –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Є—Е –ї—Г—З–µ–є –љ–∞ 43% —Б–Њ—Б—В–Њ–Є—В –Є–Ј —Н–љ–µ—А–≥–Є–Є –њ—А–Њ—В–Њ–љ–Њ–≤, –љ–∞ 23% вАФ –Є–Ј —Н–љ–µ—А–≥–Є–Є –∞–ї—М—Д–∞-—З–∞—Б—В–Є—Ж –Є 34% –Є–Ј —Н–љ–µ—А–≥–Є–Є, –њ–µ—А–µ–љ–Њ—Б–Є–Љ–Њ–є –Њ—Б—В–∞–ї—М–љ—Л–Љ–Є —З–∞—Б—В–Є—Ж–∞–Љ–Є.
–Я—А–µ–і—Б—В–∞–≤–Є–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є –Ї–∞–Ї —Б–Њ—Б—Г–і, –≤ –Ї–Њ—В–Њ—А–Њ–Љ –Љ–µ–ґ–і—Г —А–∞–Ј–ї–Є—З–љ—Л–Љ–Є –≥–∞–Ј–∞–Љ–Є —Г–±—А–∞–ї–Є –њ–µ—А–µ–≥–Њ—А–Њ–і–Ї–Є. –Ґ–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —Б–Љ–µ—Б–Є –≥–∞–Ј–Њ–≤ –і–Њ–ї–ґ–љ–∞ –Њ–њ—А–µ–і–µ–ї–Є—В—М—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–∞–Љ:
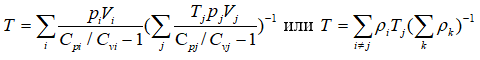
–Ф–ї—П –Њ–і–љ–Њ–∞—В–Њ–Љ–љ—Л—Е –≥–∞–Ј–Њ–≤, –Ї–Њ–≥–і–∞ —Б—Г–Љ–Љ–∞ –≤–љ—Г—В—А–µ–љ–љ–Є—Е —Н–љ–µ—А–≥–Є–є –љ–µ –Љ–µ–љ—П–µ—В—Б—П, —А–∞–≤–љ–Њ–≤–µ—Б–љ–∞—П —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Є–Ј –ї–µ–≥–Ї–Њ –њ–Њ–ї—Г—З–∞–µ–Љ–Њ–≥–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П:
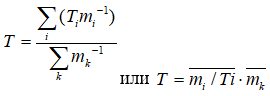
–≥–і–µ 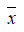 вАФ —Б—А–µ–і–љ–µ–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –≤–µ–ї–Є—З–Є–љ
вАФ —Б—А–µ–і–љ–µ–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ –≤–µ–ї–Є—З–Є–љ 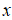 . –Ь–µ–ґ–і—Г —В–µ–Љ —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –Љ–µ–ґ–Ј–≤–µ–Ј–і–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ вАФ 4 K, –≤ —В–Њ –≤—А–µ–Љ—П –Ї–∞–Ї —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —А–µ–ї–Є–Ї—В–Њ–≤–Њ–≥–Њ –Є–Ј–ї—Г—З–µ–љ–Є—П вАФ 2,7 K, —В.–µ. –Ј–∞ –Љ–Є–ї–ї–Є–∞—А–і—Л –ї–µ—В —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ —В–∞–Ї –Є –љ–µ —Г—Б—В–∞–љ–Њ–≤–Є–ї–Њ—Б—М (—Б–Љ. —В–∞–Ї–ґ–µ [5, —Б.
. –Ь–µ–ґ–і—Г —В–µ–Љ —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –Љ–µ–ґ–Ј–≤–µ–Ј–і–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ вАФ 4 K, –≤ —В–Њ –≤—А–µ–Љ—П –Ї–∞–Ї —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —А–µ–ї–Є–Ї—В–Њ–≤–Њ–≥–Њ –Є–Ј–ї—Г—З–µ–љ–Є—П вАФ 2,7 K, —В.–µ. –Ј–∞ –Љ–Є–ї–ї–Є–∞—А–і—Л –ї–µ—В —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ —В–∞–Ї –Є –љ–µ —Г—Б—В–∞–љ–Њ–≤–Є–ї–Њ—Б—М (—Б–Љ. —В–∞–Ї–ґ–µ [5, —Б.
–Ю—Е–ї–∞–ґ–і–µ–љ–Є–µ –Т—Б–µ–ї–µ–љ–љ–Њ–є
–Т –њ–Њ–њ—Г–ї—П—А–љ—Л—Е –ї–µ–Ї—Ж–Є—П—Е (–љ–∞–њ—А–Є–Љ–µ—А, –Р. –Ы–Є–љ–і–µ) –њ—А–Є–љ—П—В–Њ —Г–Ї–∞–Ј—Л–≤–∞—В—М, —З—В–Њ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П –Т—Б–µ–ї–µ–љ–љ–Њ–є —Г–±—Л–≤–∞–µ—В –њ–Њ –Ј–∞–Ї–Њ–љ—Г 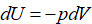 , –≥–і–µ V вАФ –Њ–±—К–µ–Љ –≤—Б–µ–ї–µ–љ–љ–Њ–є, –µ—Б–ї–Є —В–∞–Ї–Њ–≤–Њ–є –Љ–Њ–ґ–µ—В –±—Л—В—М, —А вАФ –і–∞–≤–ї–µ–љ–Є–µ, –Њ–љ–Њ –њ–Њ—Б—В–Њ—П–љ–љ–Њ. –°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є –Њ–±—К–µ–Љ–∞ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П –Є —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —Г–±—Л–≤–∞—О—В. –Ю–і–љ–∞–Ї–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –Њ –њ–Њ—Б—В–Њ—П–љ—Б—В–≤–µ –і–∞–≤–ї–µ–љ–Є—П вАФ –Њ—И–Є–±–Ї–∞, —А–∞—Б—И–Є—А–µ–љ–Є–µ –Т—Б–µ–ї–µ–љ–љ–Њ–є вАФ –∞–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Є–є –њ—А–Њ—Ж–µ—Б—Б, –Ї–Њ–≥–і–∞ —Б–Є—Б—В–µ–Љ–∞ –љ–µ –Њ—В–і–∞–µ—В —В–µ–њ–ї–Њ—В—Г –Є –љ–µ –њ–Њ–ї—Г—З–∞–µ—В –µ–µ –Є–Ј–≤–љ–µ. –Я—А–Є –∞–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Њ–Љ —А–∞—Б—И–Є—А–µ–љ–Є–Є –Є–і–µ–∞–ї—М–љ–Њ–≥–Њ –≥–∞–Ј–∞
, –≥–і–µ V вАФ –Њ–±—К–µ–Љ –≤—Б–µ–ї–µ–љ–љ–Њ–є, –µ—Б–ї–Є —В–∞–Ї–Њ–≤–Њ–є –Љ–Њ–ґ–µ—В –±—Л—В—М, —А вАФ –і–∞–≤–ї–µ–љ–Є–µ, –Њ–љ–Њ –њ–Њ—Б—В–Њ—П–љ–љ–Њ. –°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є –Њ–±—К–µ–Љ–∞ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П –Є —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —Г–±—Л–≤–∞—О—В. –Ю–і–љ–∞–Ї–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –Њ –њ–Њ—Б—В–Њ—П–љ—Б—В–≤–µ –і–∞–≤–ї–µ–љ–Є—П вАФ –Њ—И–Є–±–Ї–∞, —А–∞—Б—И–Є—А–µ–љ–Є–µ –Т—Б–µ–ї–µ–љ–љ–Њ–є вАФ –∞–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Є–є –њ—А–Њ—Ж–µ—Б—Б, –Ї–Њ–≥–і–∞ —Б–Є—Б—В–µ–Љ–∞ –љ–µ –Њ—В–і–∞–µ—В —В–µ–њ–ї–Њ—В—Г –Є –љ–µ –њ–Њ–ї—Г—З–∞–µ—В –µ–µ –Є–Ј–≤–љ–µ. –Я—А–Є –∞–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Њ–Љ —А–∞—Б—И–Є—А–µ–љ–Є–Є –Є–і–µ–∞–ї—М–љ–Њ–≥–Њ –≥–∞–Ј–∞ 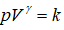 , –≥–і–µ k вАФ –Ї–Њ–љ—Б—В–∞–љ—В–∞. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ
, –≥–і–µ k вАФ –Ї–Њ–љ—Б—В–∞–љ—В–∞. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ 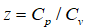 . –Ґ–Њ –µ—Б—В—М, –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є –Њ–±—К–µ–Љ–∞ –і–∞–≤–ї–µ–љ–Є–µ —Г–Љ–µ–љ—М—И–∞–µ—В—Б—П. –°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Љ–µ–µ—В –≤–Є–і:
. –Ґ–Њ –µ—Б—В—М, –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є –Њ–±—К–µ–Љ–∞ –і–∞–≤–ї–µ–љ–Є–µ —Г–Љ–µ–љ—М—И–∞–µ—В—Б—П. –°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Љ–µ–µ—В –≤–Є–і:
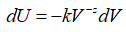
–Ю—В—Б—О–і–∞ —Б–љ–Є–ґ–µ–љ–Є–µ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Н–љ–µ—А–≥–Є–Є –њ—А–Є —А–∞—Б—И–Є—А–µ–љ–Є–Є –Є–Љ–µ–µ—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –Є–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А:
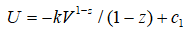
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ —Б–Є–ї—Л –љ–∞ –Љ–љ–Њ–≥–Њ –њ–Њ—А—П–і–Ї–Њ–≤ —Б–ї–∞–±–µ–µ –≤–∞–љ-–і–µ—А-–≤–∞–∞–ї—М—Б–Њ–≤—Л—Е, –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –Т—Б–µ–ї–µ–љ–љ—Г—О –Ї–∞–Ї –Є–і–µ–∞–ї—М–љ—Л–є –≥–∞–Ј.
–Ю–і–љ–∞–Ї–Њ –і–µ–ї–Њ –≤ —В–Њ–Љ, —З—В–Њ –µ—Б–ї–Є –њ—А–µ–і—Б—В–∞–≤–Є—В—М —Б–Њ–і–µ—А–ґ–Є–Љ–Њ–µ –Т—Б–µ–ї–µ–љ–љ–Њ–є –Ї–∞–Ї –Є–і–µ–∞–ї—М–љ—Л–є –≥–∞–Ј, —В–Њ –µ–≥–Њ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П –њ—А–Є —А–∞—Б—И–Є—А–µ–љ–Є–Є –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –Њ–±—К–µ–Љ–∞, –Ї–∞–Ї –±—Л–ї–Њ –њ–Њ–Ї–∞–Ј–∞–љ–Њ –Ф–ґ–Њ—Г–ї–µ–Љ –µ—Й–µ –≤ 1845 –≥–Њ–і—Г.
–Т —А–µ–∞–ї—М–љ–Њ–Љ –≥–∞–Ј–µ
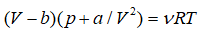
–Я–Њ—Б—В–Њ—П–љ–љ—Л–µ –Т–∞–љ-–і–µ—А-–Т–∞–∞–ї—М—Б–∞ –∞ –Є b —Г—З–Є—В—Л–≤–∞—О—В –њ—А–Є—В—П–ґ–µ–љ–Є–µ –Љ–µ–ґ–і—Г –Љ–Њ–ї–µ–Ї—Г–ї–∞–Љ–Є –љ–∞ –±–Њ–ї—М—И–Є—Е —А–∞—Б—Б—В–Њ—П–љ–Є—П—Е (–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –∞) –Є —Б–Є–ї—М–љ–Њ–µ –Њ—В—В–∞–ї–Ї–Є–≤–∞–љ–Є–µ –љ–∞ –Љ–∞–ї—Л—Е (–њ–Њ—Б—В–Њ—П–љ–љ–∞—П b). –≠—В–Њ –Њ—В—В–∞–ї–Ї–Є–≤–∞–љ–Є–µ –і–µ–ї–∞–µ—В –љ–µ–і–Њ—Б—В—Г–њ–љ—Л–Љ –≤–љ—Г—В—А–µ–љ–љ–µ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Љ–Њ–ї–µ–Ї—Г–ї—Л –і–ї—П –Њ—Б—В–∞–ї—М–љ—Л—Е –Љ–Њ–ї–µ–Ї—Г–ї –Є —Г–Љ–µ–љ—М—И–∞–µ—В –Њ–±—Й–Є–є —Б–≤–Њ–±–Њ–і–љ—Л–є –Њ–±—К–µ–Љ.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤–Њ –≤—Б–µ–ї–µ–љ–љ–Њ–є –њ—А–Њ–љ–Є–Ї–љ–Њ–≤–µ–љ–Є–µ –≤–Њ –≤–љ—Г—В—А–µ–љ–љ–Є–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ –љ–µ –≥—А–Њ–Ј–Є—В, —В–Њ –њ–Њ—Б—В–Њ—П–љ–љ—Г—О b –Љ–Њ–ґ–љ–Њ —Б–Љ–µ–ї–Њ –њ–Њ–ї–Њ–ґ–Є—В—М —А–∞–≤–љ–Њ–є –љ—Г–ї—О:
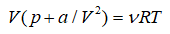
–Я—А–Є—З–µ–Љ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –∞ –њ–µ—А–µ—Б—В–∞–µ—В –±—Л—В—М –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є: a = 1/r2, 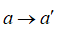 , –Є
, –Є
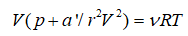 ,
,
–≥–і–µ r вАФ —А–∞–і–Є—Г—Б –Т—Б–µ–ї–µ–љ–љ–Њ–є, 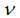 вАФ —З–Є—Б–ї–Њ –Љ–Њ–ї–µ–є,
вАФ —З–Є—Б–ї–Њ –Љ–Њ–ї–µ–є, 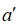 вАФ –љ–Њ–≤–∞—П –Ї–Њ–љ—Б—В–∞–љ—В–∞.
вАФ –љ–Њ–≤–∞—П –Ї–Њ–љ—Б—В–∞–љ—В–∞.
–Ю—Ж–µ–љ–Є–Љ —Б–Ї–Њ—А–Њ—Б—В—М –Є–Ј–Љ–µ–љ–µ–љ–Є—П —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –Т—Б–µ–ї–µ–љ–љ–Њ–є.
–Т —А–µ–∞–ї—М–љ–Њ–Љ –≥–∞–Ј–µ –њ—А–Є —А–∞—Б—И–Є—А–µ–љ–Є–Є –≤ –њ—Г—Б—В–Њ—В—Г —Б—А–µ–і–љ–µ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –Љ–Њ–ї–µ–Ї—Г–ї–∞–Љ–Є —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П, —Б–Є–ї—Л –њ—А–Є—В—П–ґ–µ–љ–Є—П —Б–Њ–≤–µ—А—И–∞—О—В –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Г—О —А–∞–±–Њ—В—Г, –Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ–ї–љ–∞—П –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П –Њ—Б—В–∞–µ—В—Б—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є, –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П –Љ–Њ–ї–µ–Ї—Г–ї, –∞ –Ј–љ–∞—З–Є—В, –Є —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –≥–∞–Ј–∞, —Г–Љ–µ–љ—М—И–∞—О—В—Б—П.
–Т–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є —А–Њ–ї—М —Б–Є–ї –Т–∞–љ-–і–µ—А-–Т–∞–∞–ї—М—Б–∞ –Є–≥—А–∞—О—В —Б–Є–ї—Л –≥—А–∞–≤–Є—В–∞—Ж–Є–Є, –њ—А–Є—З–µ–Љ –Є—Б–Ї–ї—О—З–Є—В–µ–ї—М–љ–Њ –љ–∞ ¬Ђ–њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є¬ї, —В.–Ї. ¬Ђ–≤–љ—Г—В—А–Є¬ї –Т—Б–µ–ї–µ–љ–љ–Њ–є —Б—Г–Љ–Љ–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л—Е —Б–Є–ї –≤ —В–Њ—З–Ї–µ —А–∞–≤–љ–∞ –љ—Г–ї—О –≤ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–Є –љ—М—О—В–Њ–љ–Њ–≤—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Є –љ–µ —А–∞–≤–љ–∞ –љ—Г–ї—О –ї–Є—И—М –≤ –Ю–Ґ–Ю. –Ю–і–љ–∞–Ї–Њ –≥–Њ–≤–Њ—А–Є—В—М –Њ —Б–љ–Є–ґ–µ–љ–Є–Є –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Њ–є —Н–љ–µ—А–≥–Є–Є —Н–ї–µ–Љ–µ–љ—В–Њ–≤, —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є—Е –Т—Б–µ–ї–µ–љ–љ—Г—О, –Ј–∞—В—А—Г–і–љ–Є—В–µ–ї—М–љ–Њ. –≠—В–Њ, –≤–Њ-–њ–µ—А–≤—Л—Е, –≥–∞–ї–∞–Ї—В–Є–Ї–Є, –Ї–Њ—В–Њ—А—Л–µ –≤ –≤—Л–і–µ–ї–µ–љ–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ –Њ—В—Б—З–µ—В–∞ –љ–µ —В–Њ–ї—М–Ї–Њ –љ–µ —Б–љ–Є–ґ–∞—О—В —Б–≤–Њ–Є —Б–Ї–Њ—А–Њ—Б—В–Є, –љ–Њ –њ—А–Є —Г–і–∞–ї–µ–љ–Є–Є –Њ—В —В–Њ—З–Ї–Є –Њ—В—Б—З–µ—В–∞ –Є—Е —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В.
–Ь–Њ–ґ–љ–Њ –≥–Њ–≤–Њ—А–Є—В—М –Њ –Љ–µ–ґ–Ј–≤–µ–Ј–і–љ–Њ–є –њ—Л–ї–Є, —А–µ–ї–Є–Ї—В–Њ–≤–Њ–Љ –Є–Ј–ї—Г—З–µ–љ–Є–Є, —Н–ї–µ–Ї—В—А–Њ–љ–∞—Е, –њ—А–Њ—В–Њ–љ–∞—Е, —П–і—А–∞—Е –≥–µ–ї–Є—П, –Є–Ј–ї—Г—З–µ–љ–Є–Є –Ј–≤–µ–Ј–і, —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –≤—Б–µ–≥–Њ —Н—В–Њ–≥–Њ —Б–Њ–і–µ—А–ґ–Є–Љ–Њ–≥–Њ, –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ, —В–µ—А—П–µ—В —В–µ–Љ–њ–µ—А–∞—В—Г—А—Г, –љ–µ—Б–Љ–Њ—В—А—П –љ–∞ –њ—А–Њ–і–Њ–ї–ґ–∞—О—Й–Є–є—Б—П –њ—А–Њ—Ж–µ—Б—Б –Ј–≤–µ–Ј–і–Њ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П.
–Ь–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –і–∞–≤–ї–µ–љ–Є–µ –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є –Т–∞–љ-–і–µ—А-–Т–∞–∞–ї—М—Б–∞ –Ї–∞–Ї –≤–љ—Г—В—А–µ–љ–љ–µ–µ –і–∞–≤–ї–µ–љ–Є–µ, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–Њ–µ –Ј–∞–Ї–Њ–љ–Њ–Љ –•–∞–±–±–ї–∞. –Х—Б–ї–Є –њ—А–µ–і—Б—В–∞–≤–Є—В—М –Т—Б–µ–ї–µ–љ–љ—Г—О –≤ –≤–Є–і–µ —И–∞—А–∞, –≤—Б—П –Љ–∞—Б—Б–∞ –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤ —Ж–µ–љ—В—А–µ, —В–Њ –≤ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ —Б–ї—Г—З–∞–µ –Є –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ —А–∞–±–Њ—В–∞, —Б–Њ–≤–µ—А—И–∞–µ–Љ–∞—П –њ—А–Є —А–∞—Б—И–Є—А–µ–љ–Є–Є –Т—Б–µ–ї–µ–љ–љ–Њ–є:
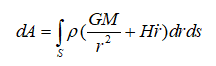
(–Х—Б–ї–Є –Љ–∞—Б—Б—Г ¬Ђ—А–∞–Ј–Љ–∞–Ј–∞—В—М¬ї —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –њ–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є, —В–Њ –њ–Њ–ї—Г—З–Є–Љ –і–ї—П —Б—А–µ–і–љ–µ–є –њ–ї–Њ—В–љ–Њ—Б—В–Є –≤–µ–ї–Є—З–Є–љ—Г –њ–Њ—А—П–і–Ї–∞ 10-31 –≥/—Б–Љ3. –Я–Њ –і—А—Г–≥–Њ–є –≤–µ—А—Б–Є–Є —Б—З–Є—В–∞–µ—В—Б—П, —З—В–Њ –≤ –≥–∞–ї–∞–Ї—В–Є–Ї–∞—Е –і–Њ–ї–ґ–љ–Њ –±—Л—В—М –Љ–љ–Њ–≥–Њ –љ–µ–≤–Є–і–Є–Љ–Њ–≥–Њ –≤–µ—Й–µ—Б—В–≤–∞, –Є–љ–∞—З–µ –љ–µ–ї—М–Ј—П –њ–Њ–љ—П—В—М, –њ–Њ—З–µ–Љ—Г –љ–µ–Ї–Њ—В–Њ—А—Л–µ –≥–∞–ї–∞–Ї—В–Є–Ї–Є –≥—А—Г–њ–њ–Є—А—Г—О—В—Б—П –≤ —Б–Є—Б—В–µ–Љ—Л —Б–Њ —Б–њ—Г—В–љ–Є–Ї–∞–Љ–Є. –Х—Б–ї–Є —В–∞–Ї–∞—П —В–Њ—З–Ї–∞ –Ј—А–µ–љ–Є—П –њ—А–∞–≤–Є–ї—М–љ–∞, —В–Њ –Њ—Ж–µ–љ–Ї–∞ —Б—А–µ–і–љ–µ–є –њ–ї–Њ—В–љ–Њ—Б—В–Є –≤–µ—Й–µ—Б—В–≤–∞ —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П –і–Њ 10-30 –≥/—Б–Љ3, —В. –µ. –і–Њ вАФ 1 –љ—Г–Ї–ї–Њ–љ/–Љ3).
–Я—А–Є–Љ–µ–Љ —Б—А–µ–і–љ–µ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –≥–∞–ї–∞–Ї—В–Є–Ї–∞–Љ–Є 2 –Ь–њ–Ї (–њ–Њ –і—А—Г–≥–Є–Љ –і–∞–љ–љ—Л–Љ вАФ 0,7 –Ь–њ–Ї). –Я—А–Є–Љ–µ–Љ —Б—А–µ–і–љ—О—О –Љ–∞—Б—Б—Г m –≥–∞–ї–∞–Ї—В–Є–Ї–Є –Ј–∞ 300 –Љ–ї—А–і. —Б–Њ–ї–љ–µ—З–љ—Л—Е –Љ–∞—Б—Б: 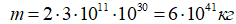 . –Т –Њ–і–љ–Њ–Љ –Ї–≤–∞–і—А–∞—В–µ
. –Т –Њ–і–љ–Њ–Љ –Ї–≤–∞–і—А–∞—В–µ 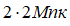 —Б–Њ–і–µ—А–ґ–Є—В—Б—П –Њ–і–љ–∞ –≥–∞–ї–∞–Ї—В–Є–Ї–∞. –†–∞–і–Є—Г—Б –Т—Б–µ–ї–µ–љ–љ–Њ–є R вАФ 78 –Љ–ї—А–і. —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В, –Є–ї–Є 1016 –Љ —Е 78√Ч109 = 7,4√Ч1026 –Љ. –Я–ї–Њ—Й–∞–і—М –Њ–і–љ–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞
—Б–Њ–і–µ—А–ґ–Є—В—Б—П –Њ–і–љ–∞ –≥–∞–ї–∞–Ї—В–Є–Ї–∞. –†–∞–і–Є—Г—Б –Т—Б–µ–ї–µ–љ–љ–Њ–є R вАФ 78 –Љ–ї—А–і. —Б–≤–µ—В–Њ–≤—Л—Е –ї–µ—В, –Є–ї–Є 1016 –Љ —Е 78√Ч109 = 7,4√Ч1026 –Љ. –Я–ї–Њ—Й–∞–і—М –Њ–і–љ–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞ 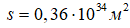 .
. 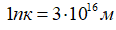 . –Ш—В–Њ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–љ–∞—П –њ–ї–Њ—В–љ–Њ—Б—В—М
. –Ш—В–Њ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–љ–∞—П –њ–ї–Њ—В–љ–Њ—Б—В—М 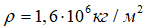 , —З—В–Њ –љ–∞ 9 –њ–Њ—А—П–і–Ї–Њ–≤ –Љ–µ–љ—М—И–µ, —З–µ–Љ –≤ –Ь–ї–µ—З–љ–Њ–Љ –њ—Г—В–Є. –Я–ї–Њ—Й–∞–і—М —Б—Д–µ—А—Л
, —З—В–Њ –љ–∞ 9 –њ–Њ—А—П–і–Ї–Њ–≤ –Љ–µ–љ—М—И–µ, —З–µ–Љ –≤ –Ь–ї–µ—З–љ–Њ–Љ –њ—Г—В–Є. –Я–ї–Њ—Й–∞–і—М —Б—Д–µ—А—Л 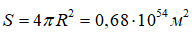 .
.
–Ґ–Њ–≥–і–∞, –µ—Б–ї–Є —Б—З–Є—В–∞—В—М –≥–∞–ї–∞–Ї—В–Є–Ї–Є —В–Њ—З–µ—З–љ—Л–Љ–Є
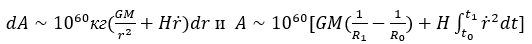
–Ш—Б–њ–Њ–ї—М–Ј—Г–µ–Љ –µ—Й–µ —А–∞–Ј –Ј–∞–Ї–Њ–љ –•–∞–±–±–ї–∞:
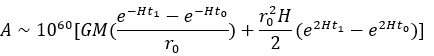
–≥–і–µ r0 вАФ –Ї–Њ–љ—Б—В–∞–љ—В–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П. –Х—Б–ї–Є —Б–µ–≥–Њ–і–љ—П—И–љ–Є–є –Љ–Њ–Љ–µ–љ—В –≤—А–µ–Љ–µ–љ–Є –њ—А–Є–љ—П—В—М –Ј–∞ —В–Њ—З–Ї—Г –Њ—В—Б—З–µ—В–∞ t0 = 0 –Є r0 = R вАФ —Б–Њ–≤—А–µ–Љ–µ–љ–љ—Л–є —А–∞–і–Є—Г—Б –Т—Б–µ–ї–µ–љ–љ–Њ–є, —В–Њ
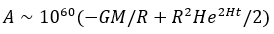
–Я—А–Є –±–Њ–ї—М—И–Є—Е R —А–∞–±–Њ—В–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Е–∞–±–±–ї–Њ–≤—Б–Ї–Є–Љ –≤–Ї–ї–∞–і–Њ–Љ, —З—В–Њ –±—Л–ї–Њ —П—Б–љ–Њ —Б —Б–∞–Љ–Њ–≥–Њ –љ–∞—З–∞–ї–∞, –Є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤ –∞–і–Є–∞–±–∞—В–Є—З–µ—Б–Ї–Њ–Љ –њ—А–Њ—Ж–µ—Б—Б–µ
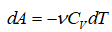 ,
,
—В–Њ –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ, –≤ –≤–Є–і—Г –Љ–љ–Њ–ґ–Є—В–µ–ї—П 1060 —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –Т—Б–µ–ї–µ–љ–љ–Њ–є –њ–Њ—З—В–Є –Љ–≥–љ–Њ–≤–µ–љ–љ–Њ –і–Њ–ї–ґ–љ–∞ —Г–њ–∞—Б—В—М –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –і–Њ –љ—Г–ї—П, —З—В–Њ –љ–µ –љ–∞–±–ї—О–і–∞–µ—В—Б—П. –Х—Б–ї–Є –Ј–∞ –Є—Б—Е–Њ–і–љ—Г—О –њ—А–Є–љ—П—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–љ—Г—О –њ–ї–Њ—В–љ–Њ—Б—В—М –≤ –Ь–ї–µ—З–љ–Њ–Љ –њ—Г—В–Є, –њ–Њ—А—П–і–Ї–∞ 70 –Љ–∞—Б—Б –°–Њ–ї–љ—Ж–∞ –љ–∞ –Ї–≤–∞–і—А–∞—В–љ—Л–є –њ–∞—А—Б–µ–Ї [6, —Б. 462.], —В–Њ –Љ–љ–Њ–ґ–Є—В–µ–ї—М –µ—Й–µ –±–Њ–ї—М—И–µ —Г–≤–µ–ї–Є—З–Є—В—Б—П, –і–Њ 1069. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–є –њ–Њ–і—Е–Њ–і –љ–µ –њ—А–Є–Љ–µ–љ–Є–Љ –Ї–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є –Ї–∞–Ї –Ї —Ж–µ–ї–Њ–Љ—Г.
–†–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–∞—П —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞
–Т –њ–Њ–і—Е–Њ–і–µ –Я–ї–∞–љ–Ї–∞-–≠–є–љ—И—В–µ–є–љ–∞ —Б–Є—Б—В–µ–Љ–∞ –±—Г–і–µ—В —Е–Њ–ї–Њ–і–љ–µ–µ —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –љ–∞–±–ї—О–і–∞—В–µ–ї—П, –і–≤–Є–ґ—Г—Й–µ–≥–Њ—Б—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –µ–µ, –∞ –њ–Њ—В–Њ–Ї —В–µ–њ–ї–∞ –±—Г–і–µ—В –Љ–µ–љ—М—И–µ, 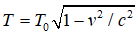 . –Т –њ–Њ–і—Е–Њ–і–µ –Ю—В—В–∞ –Ј–∞–Ї–Њ–љ—Л –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Њ–±—А–∞—В–љ—Л. –Х—Б–ї–Є –Ј–∞
. –Т –њ–Њ–і—Е–Њ–і–µ –Ю—В—В–∞ –Ј–∞–Ї–Њ–љ—Л –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Њ–±—А–∞—В–љ—Л. –Х—Б–ї–Є –Ј–∞ 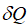 –њ—А–Є–љ—П—В—М –њ–Њ–ї–љ—Г—О –њ–µ—А–µ–і–∞–љ–љ—Г—О —Н–љ–µ—А–≥–Є—О, —В–Њ
–њ—А–Є–љ—П—В—М –њ–Њ–ї–љ—Г—О –њ–µ—А–µ–і–∞–љ–љ—Г—О —Н–љ–µ—А–≥–Є—О, —В–Њ 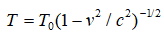 . –Ґ–Њ–≥–і–∞ –і–ї—П –і–≤–Є–ґ—Г—Й–µ–≥–Њ—Б—П –љ–∞–±–ї—О–і–∞—В–µ–ї—П —Б–Є—Б—В–µ–Љ–∞ –≥–Њ—А—П—З–µ–µ, –∞ —В–µ–њ–ї–Њ–≤–Њ–є –њ–Њ—В–Њ–Ї –±–Њ–ї—М—И–µ:
. –Ґ–Њ–≥–і–∞ –і–ї—П –і–≤–Є–ґ—Г—Й–µ–≥–Њ—Б—П –љ–∞–±–ї—О–і–∞—В–µ–ї—П —Б–Є—Б—В–µ–Љ–∞ –≥–Њ—А—П—З–µ–µ, –∞ —В–µ–њ–ї–Њ–≤–Њ–є –њ–Њ—В–Њ–Ї –±–Њ–ї—М—И–µ: 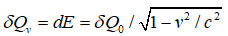
–£—В–≤–µ—А–ґ–і–∞–µ—В—Б—П, —З—В–Њ —А–∞–Ј–љ–Њ—З—В–µ–љ–Є—П —Б–≤—П–Ј–∞–љ—Л —Н—В–Њ —Б –њ—А–Њ–Є–Ј–≤–Њ–ї–Њ–Љ –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–Є –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —В–µ–њ–ї–Њ—В—Л. –Я–µ—А–µ–і–∞–≤–∞–µ–Љ—Г—О —В–µ–њ–ї–Њ—В—Г –≤ –°–Ґ–Ю –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –ї–Є–±–Њ –њ—А–Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–Љ –Є–Љ–њ—Г–ї—М—Б–µ (–Ї–∞–Ї –њ—А–µ–і–ї–Њ–ґ–Є–ї–Є –Я–ї–∞–љ–Ї –Є –≠–є–љ—И—В–µ–є–љ), –ї–Є–±–Њ –њ—А–Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є. –Ы–∞–љ–і—Б–±–µ—А–≥ –њ–Њ–ї–∞–≥–∞–ї, —З—В–Њ —В–µ–Љ–њ–µ—А–∞—В—Г—А—Г —Б–ї–µ–і—Г–µ—В —Б—З–Є—В–∞—В—М –ї–Њ—А–µ–љ—Ж–µ–≤—Л–Љ –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–Љ, —В–Њ–≥–і–∞ –Ї–∞–Ї –і–ї—П –њ–µ—А–µ–і–∞–љ–љ–Њ–≥–Њ —В–µ–њ–ї–∞ –Њ—Б—В–∞–µ—В—Б—П –≤–µ—А–љ—Л–Љ —Б—В–∞—А–Њ–µ –њ–ї–∞–љ–Ї–Њ–≤—Б–Ї–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ. –Ф–µ –С—А–Њ–є–ї—М –≤ –і–∞–љ–љ–Њ–Љ –≤–Њ–њ—А–Њ—Б–µ –Є—Б—Е–Њ–і–Є–ї –Є–Ј —В–Њ–≥–Њ, —З—В–Њ –і–∞–≤–ї–µ–љ–Є–µ –љ–µ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –≤–љ—Г—В—А–Є —Б–Є—Б—В–µ–Љ—Л, –∞ –ї–Є—И—М, –љ–∞ –≥—А–∞–љ–Є—Ж–µ, –Ь—С–ї–ї–µ—А –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є–ї, —З—В–Њ –≤
–Я–Њ—П–≤–ї—П—О—В—Б—П –љ–Њ–≤—Л–µ —А–∞–±–Њ—В—Л, –≥–і–µ –Њ–±—К–µ–Љ –ї–Њ—А–µ–љ—Ж-–Є–љ–≤–∞—А–Є–∞–љ—В–µ–љ, –љ–Њ —Н–Ї—Б—В–µ–љ—Б–Є–≤–µ–љ [4].
–Ґ–Њ–ї–Љ–µ–љ —Б–ї–µ–і—Г–µ—В –Я–ї–∞–љ–Ї—Г –Є –≠–є–љ—И—В–µ–є–љ—Г –Є –∞—А–≥—Г–Љ–µ–љ—В–Є—А—Г–µ—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: –≤ –°–Ґ–Ю –Є–Љ–њ—Г–ї—М—Б –Љ–Њ–ґ–µ—В –Љ–µ–љ—П—В—М—Б—П –Є –њ—А–Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є, –µ—Б–ї–Є –Є–Ј–Љ–µ–љ—П–µ—В—Б—П —Н–љ–µ—А–≥–Є—П —Б–Є—Б—В–µ–Љ—Л, –∞ —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–Њ–ї–ґ–љ–∞ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞—В—М –≤–љ–µ—И–љ—П—П —Б–Є–ї–∞, –Ї–Њ—В–Њ—А–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В —А–∞–±–Њ—В—Г –Є –њ–Њ–і–і–µ—А–ґ–Є–≤–∞–µ—В –њ–Њ—Б—В–Њ—П–љ–љ—Г—О —Б–Ї–Њ—А–Њ—Б—В—М.
—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є –њ–Њ–њ—А–∞–≤–Ї–Њ–є
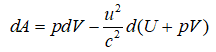
–≥–і–µ u вАФ —Б–Ї–Њ—А–Њ—Б—В—М –і–≤–Є–ґ–µ–љ–Є—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –љ–∞–±–ї—О–і–∞—В–µ–ї—П [8, —Б. 163].
–Я–µ—А–µ–і–∞—З–∞ —Н–љ–µ—А–≥–Є–Є –Њ—В –Њ–і–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї –і—А—Г–≥–Њ–є —Б–≤—П–Ј–∞–љ–∞ —Б –Є–Ј–Љ–µ–љ–µ–љ–Є–µ–Љ –Є–Љ–њ—Г–ї—М—Б–∞ –Є –Љ–∞—Б—Б—Л.
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ —В–µ–њ–ї–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —Н–љ–µ—А–≥–Є–Є –Ј–∞ –≤—Л—З–µ—В–Њ–Љ —А–∞–±–Њ—В—Л 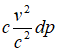 (—А вАФ –Є–Љ–њ—Г–ї—М—Б). –Т —Б–Є—Б—В–µ–Љ–µ –њ–Њ–Ї–Њ—П –њ—А–Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–Љ –Њ–±—К–µ–Љ–µ
(—А вАФ –Є–Љ–њ—Г–ї—М—Б). –Т —Б–Є—Б—В–µ–Љ–µ –њ–Њ–Ї–Њ—П –њ—А–Є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–Љ –Њ–±—К–µ–Љ–µ 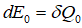 . –Т –і–≤–Є–ґ—Г—Й–µ–є—Б—П —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В [—В–∞–Љ –ґ–µ, —Б. 165]:
. –Т –і–≤–Є–ґ—Г—Й–µ–є—Б—П —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В [—В–∞–Љ –ґ–µ, —Б. 165]:
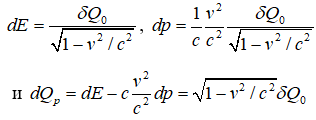
–Ф–∞–ї–µ–µ –Ґ–Њ–ї–Љ–µ–љ –њ–µ—А–µ—Е–Њ–і–Є—В –Ї –Њ–±—Й–µ–є —В–µ–Њ—А–Є–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є –Є –ї–Њ–≥–Є—З–љ–Њ —Г—В–≤–µ—А–ґ–і–∞–µ—В, —З—В–Њ –Є —В–µ–њ–ї–Њ—В–∞, –Є —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —П–≤–ї—П—О—В—Б—П —Б–Ї–∞–ї—П—А–∞–Љ–Є –Є –њ–Њ—В–Њ–Љ—Г –Є—Е –Ј–љ–∞—З–µ–љ–Є—П –љ–Є–Ї–∞–Ї –љ–µ —Б–≤—П–Ј–∞–љ—Л —Б —Б–Є—Б—В–µ–Љ–Њ–є –Њ—В—Б—З–µ—В–∞. –Ю–і–љ–∞–Ї–Њ –і–∞–ї–µ–µ –Њ–љ –њ–Њ—Б–ї–µ –љ–µ–Ї–Њ—В–Њ—А—Л—Е –≤—Л—З–Є—Б–ї–µ–љ–Є–є –њ—А–Є—Е–Њ–і–Є—В –Ї –≤—Л–≤–Њ–і—Г, —З—В–Њ –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–Љ —П–≤–ї—П–µ—В—Б—П –Њ—В–љ–Њ—И–µ–љ–Є–µ
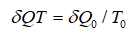
[—В–∞–Љ –ґ–µ, —Б. 304, 306]. –Ґ–µ–Љ –љ–µ –Љ–µ–љ–µ–µ, –љ–µ—Б–Љ–Њ—В—А—П –љ–∞ —В–Њ, —З—В–Њ —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ вАФ —Б–Ї–∞–ї—П—А, –Ґ–Њ–ї–Љ–µ–љ –≤—Л—З–Є—Б–ї—П–µ—В —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ —В–µ–Љ–њ–µ—А–∞—В—Г—А –≤ –≥—А–∞–≤–Є—В–Є—А—Г—О—Й–µ–є –ґ–Є–і–Ї–Њ–є —Б—Д–µ—А–µ –≤ —Б–Њ—Б—В–Њ—П–љ–Є–Є —А–∞–≤–љ–Њ–≤–µ—Б–Є—П вАФ –њ—А–Є –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є–Є –≤ —А–∞–і–Є–∞–ї—М–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є, [—В–∞–Љ –ґ–µ, —Б. 320]. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –Ґ–Њ–ї–Љ–µ–љ —Г–Ї–∞–Ј—Л–≤–∞–µ—В –љ–∞ —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є–є
–Э–Њ —В–∞–Ї–Њ–≥–Њ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М, —З—В–Њ–±—Л —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞, –љ–∞–њ—А–Є–Љ–µ—А, —Г–і–∞–ї—П—О—Й–Є—Е—Б—П –Ј–≤–µ–Ј–і –Њ–њ—А–µ–і–µ–ї—П–ї–∞—Б—М —В—А–µ–Љ—П —А–∞–Ј–љ—Л–Љ–Є —Б–њ–Њ—Б–Њ–±–∞–Љ–Є, —Б—В–∞–љ–Њ–≤—П—В—Б—П –ї–Є –≤ –°–Ґ–Ю –Њ–љ–Є —В–µ–њ–ї–µ–µ, —Е–Њ–ї–Њ–і–љ–µ–µ –Є–ї–Є –љ–µ –Љ–µ–љ—П—О—В —В–µ–Љ–њ–µ—А–∞—В—Г—А—Г –њ—А–Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П—Е –Ы–Њ—А–µ–љ—Ж–∞, —Н—В–Њ –Љ–≥–љ–Њ–≤–µ–љ–љ–Њ –±—Л —Б–Ї–∞–Ј–∞–ї–Њ—Б—М –љ–∞ –Є—Е —Б–њ–µ–Ї—В—А–∞—Е. –Ю—В–Љ–µ—В–Є–Љ, —З—В–Њ, –љ–∞–њ—А–Є–Љ–µ—А, –≤ [9, 10] —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–∞—П —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –љ–µ —Г–њ–Њ–Љ–Є–љ–∞–µ—В—Б—П.
–Ф–µ–ї–Њ –≤ —В–Њ–Љ, —З—В–Њ –≤ –°–Ґ–Ю –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї —А–∞–Ј–љ–Њ—Б—В—М –њ–Њ–ї–љ–Њ–є —Н–љ–µ—А–≥–Є–Є –Є —Н–љ–µ—А–≥–Є–Є –њ–Њ–Ї–Њ—П:
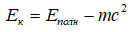 .
.
–Т —Б–Є—Б—В–µ–Љ–µ –њ–Њ–Ї–Њ—П—Й–Є—Е—Б—П —З–∞—Б—В–Є—Ж —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ —А–∞–≤–љ–∞ –љ—Г–ї—О, –∞ —Н–љ–µ—А–≥–Є—П –њ–Њ–Ї–Њ—П вАФ –љ–µ—В. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤—Л—З–Є—В–∞—В—М –љ—Г–ґ–љ–Њ –љ–µ —В–∞–Є–љ—Б—В–≤–µ–љ–љ—Г—О —А–∞–±–Њ—В—Г –≤–љ–µ—И–љ–Є—Е —Б–Є–ї, –∞ —Н–љ–µ—А–≥–Є—О –њ–Њ–Ї–Њ—П, –Ї–Њ—В–Њ—А–∞—П –Ї —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–µ –љ–µ –Є–Љ–µ–µ—В –Њ—В–љ–Њ—И–µ–љ–Є—П. –Ь–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –≤ –°–Ґ–Ю –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Њ—Е—А–∞–љ—П—О—В —Г—Б—А–µ–і–љ–µ–љ–љ—Л–є –Є–Љ–њ—Г–ї—М—Б. –Ґ–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –ґ–µ —П–≤–ї—П–µ—В—Б—П —Н–Ї—Б—В–µ–љ—Б–Є–≤–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–Њ–є –Є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –≤ —В–Њ—З–Ї–µ —З–µ—А–µ–Ј —Г—Б—А–µ–і–љ–µ–љ–љ—Л–є –њ–Њ –Љ–∞–ї–Њ–Љ—Г —Н–ї–µ–Љ–µ–љ—В—Г —Б–Є—Б—В–µ–Љ—Л –Ї–≤–∞–і—А–∞—В —Б–Ї–Њ—А–Њ—Б—В–Є —З–∞—Б—В–Є—Ж, –љ–∞–њ—А–Є–Љ–µ—А:
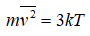
–Я—А–Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П—Е –У–∞–ї–Є–ї–µ—П —Б–Њ—Е—А–∞–љ—П–µ—В—Б—П —Г—Б—А–µ–і–љ–µ–љ–љ—Л–є –Ї–≤–∞–і—А–∞—В —Б–Ї–Њ—А–Њ—Б—В–Є, —Б–Њ—Е—А–∞–љ—П–µ—В—Б—П –Є –Ї–≤–∞–і—А–∞—В –њ—А–Њ–µ–Ї—Ж–Є–Є —Б–Ї–Њ—А–Њ—Б—В–Є –љ–∞ –≤–µ–Ї—В–Њ—А —Б–Ї–Њ—А–Њ—Б—В–Є –і–≤–Є–ґ—Г—Й–µ–є—Б—П —Б–Є—Б—В–µ–Љ—Л, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –љ–µ –Љ–µ–љ—П–µ—В—Б—П:
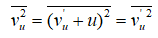
–Ґ–Њ –µ—Б—В—М: –њ–Њ—Б—В–Њ—П–љ–љ–∞—П —Б–Ї–Њ—А–Њ—Б—В—М –њ—А–Є —Г—Б—А–µ–і–љ–µ–љ–Є–Є –Њ—В–±—А–∞—Б—Л–≤–∞–µ—В—Б—П.
–Т –°–Ґ–Ю —Б–Ї–Њ—А–Њ—Б—В—М –њ—А–µ–Њ–±—А–∞–Ј—Г—О—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
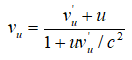
–Я—А–Є 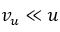 —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —Б–≤–Њ–і–Є—В—Б—П –Ї –≤–Є–і—Г:
—Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —Б–≤–Њ–і–Є—В—Б—П –Ї –≤–Є–і—Г:
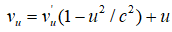 ,
,
–њ—А–Є —Г—Б—А–µ–і–љ–µ–љ–Є–Є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ—Б—В–Њ—П–љ–љ–∞—П —Б–Ї–Њ—А–Њ—Б—В—М —Б–Є—Б—В–µ–Љ—Л –Њ—В–±—А–∞—Б—Л–≤–∞–µ—В—Б—П, –њ–Њ–ї—Г—З–Є–Љ
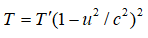
–Ґ–Њ –µ—Б—В—М, —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –≤ –і–≤–Є–ґ—Г—Й–µ–є—Б—П —Б–Є—Б—В–µ–Љ–µ –і–ї—П –њ–Њ–Ї–Њ—П—Й–µ–≥–Њ—Б—П –љ–∞–±–ї—О–і–∞—В–µ–ї—П –±—Г–і–µ—В –Љ–µ–љ—М—И–µ, —З–µ–Љ –≤ —Б–Њ–њ—Г—В—Б—В–≤—Г—О—Й–µ–є. –Т —Г–ї—М—В—А–∞—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–Љ –њ—А–µ–і–µ–ї–µ, –љ–Њ –њ—А–Є –Љ–∞–ї—Л—Е u —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ —Б–Њ—Е—А–∞–љ—П–µ—В—Б—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Г—А–∞–≤–љ–µ–љ–Є–µ, –љ–∞–њ—А–Є–Љ–µ—А, –Ъ–ї–∞–њ–µ–є—А–Њ–љ–∞-–Ь–µ–љ–і–µ–ї–µ–µ–≤–∞ –љ–µ —П–≤–ї—П–µ—В—Б—П –Ы–Њ—А–µ–љ—Ж-–Є–љ–≤–∞—А–Є–∞–љ—В–Њ–Љ.
–Я–µ—А–≤–Њ–µ –љ–∞—З–∞–ї–Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є
1. –Ч–∞–њ–Є—И–µ–Љ –њ–µ—А–≤–Њ–µ –љ–∞—З–∞–ї–Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є:
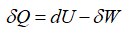
–≥–і–µ Q вАФ —В–µ–њ–ї–Њ—В–∞, U вАФ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П, W вАФ —А–∞–±–Њ—В–∞, –≤ —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–∞—Е
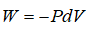 ,
,
P вАФ –і–∞–≤–ї–µ–љ–Є–µ, V вАФ –Њ–±—К–µ–Љ; –≤ –љ–µ—А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–∞—Е dW —В–Њ–ґ–µ –љ–µ —П–≤–ї—П–µ—В—Б—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї–Њ–Љ. –≠—В–Њ –ї–Є–љ–µ–є–љ–∞—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Д–Њ—А–Љ–∞ –Я—Д–∞—Д—Д–∞ –і–ї—П –і–≤—Г—Е –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е. –Ф–ї—П –і–∞–љ–љ–Њ–є –њ—Д–∞—Д—Д–Њ–≤–Њ–є —Д–Њ—А–Љ—Л —Г—Б–ї–Њ–≤–Є–µ –Є–љ—В–µ–≥—А–Є—А—Г–µ–Љ–Њ—Б—В–Є –≠–є–ї–µ—А–∞ –љ–µ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П, —В–Њ –µ—Б—В—М, 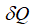 вАФ —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї, –∞ –љ–µ –њ–Њ–ї–љ—Л–є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї –љ–µ—Б—Г—Й–µ—Б—В–≤—Г—О—Й–µ–є —Д—Г–љ–Ї—Ж–Є–Є
вАФ —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї, –∞ –љ–µ –њ–Њ–ї–љ—Л–є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї –љ–µ—Б—Г—Й–µ—Б—В–≤—Г—О—Й–µ–є —Д—Г–љ–Ї—Ж–Є–Є 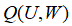 . –Я—А–Є—А–∞—Й–µ–љ–Є—П —А–∞–±–Њ—В—Л –Є —В–µ–њ–ї–Њ—В—Л –љ–µ —П–≤–ї—П—О—В—Б—П –њ–Њ–ї–љ—Л–Љ–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї–∞–Љ–Є, –Є—Е –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –Љ–∞–ї—Л–µ –њ—А–Є—А–∞—Й–µ–љ–Є—П –љ–µ –Љ–Њ–≥—Г—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –Љ–∞–ї—Л—Е –њ—А–Є—А–∞—Й–µ–љ–Є–є –∞—А–≥—Г–Љ–µ–љ—В–Њ–≤ —Б –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є, —В–Њ—З–љ–µ–µ, –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –њ–Њ–њ–∞—А–љ—Л—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є —З–∞—Б—В–љ—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –љ–∞ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е.
. –Я—А–Є—А–∞—Й–µ–љ–Є—П —А–∞–±–Њ—В—Л –Є —В–µ–њ–ї–Њ—В—Л –љ–µ —П–≤–ї—П—О—В—Б—П –њ–Њ–ї–љ—Л–Љ–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї–∞–Љ–Є, –Є—Е –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –Љ–∞–ї—Л–µ –њ—А–Є—А–∞—Й–µ–љ–Є—П –љ–µ –Љ–Њ–≥—Г—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –Љ–∞–ї—Л—Е –њ—А–Є—А–∞—Й–µ–љ–Є–є –∞—А–≥—Г–Љ–µ–љ—В–Њ–≤ —Б –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є, —В–Њ—З–љ–µ–µ, –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –њ–Њ–њ–∞—А–љ—Л—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є —З–∞—Б—В–љ—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –љ–∞ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е.
–Т—В–Њ—А–Њ–µ –љ–∞—З–∞–ї–Њ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –њ–Њ—Б—В—Г–ї–Є—А—Г–µ—В, —З—В–Њ –њ—Д–∞—Д—Д–Њ–≤–∞ —Д–Њ—А–Љ–∞ 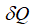 –њ—А–Є –ї—О–±–Њ–Љ —З–Є—Б–ї–µ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –≤—Б–µ–≥–і–∞ –≥–Њ–ї–Њ–љ–Њ–Љ–љ–∞ –Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–ї—П –ї—О–±–Њ–є –Ј–∞–Ї—А—Л—В–Њ–є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л —Б—Г—Й–µ—Б—В–≤—Г—О—В —Н–љ—В—А–Њ–њ–Є—П.
–њ—А–Є –ї—О–±–Њ–Љ —З–Є—Б–ї–µ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –≤—Б–µ–≥–і–∞ –≥–Њ–ї–Њ–љ–Њ–Љ–љ–∞ –Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–ї—П –ї—О–±–Њ–є –Ј–∞–Ї—А—Л—В–Њ–є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л —Б—Г—Й–µ—Б—В–≤—Г—О—В —Н–љ—В—А–Њ–њ–Є—П.
–Э–µ—А–∞–≤–љ–Њ–≤–µ—Б–љ–∞—П —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞, –Є—Б—Е–Њ–і—П –Є–Ј –њ–Њ—Б—В—Г–ї–∞—В–∞ –ї–Њ–Ї–∞–ї—М–љ–Њ–≥–Њ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –±–µ–Ј–і–Њ–Ї–∞–Ј–∞—В–µ–ї—М–љ–Њ –њ–µ—А–µ–љ–Њ—Б–Є—В –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Н–љ—В—А–Њ–њ–Є–Є, –і–∞–љ–љ–Њ–µ –і–ї—П —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –љ–∞ –љ–µ—А–∞–≤–љ–Њ–≤–µ—Б–љ—Л–µ —Б–Њ—Б—В–Њ—П–љ–Є—П.
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ —Г–Ї–∞–Ј–∞–љ–љ—Л–µ –≤—Л—И–µ –њ–Њ—Б—В—Г–ї–∞—В—Л –Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–Њ–≥—Г—В –±—Л—В—М –Њ—В–Љ–µ–љ–µ–љ—Л –≤ –Ю–Ґ–Ю. –£—А–∞–≤–љ–µ–љ–Є—П, –Њ–њ–Є—Б—Л–≤–∞—О—Й–Є–µ —Б–Є—Б—В–µ–Љ—Г –≤ –Ю–Ґ–Ю, –љ–µ –Њ–±—П–Ј–∞–љ—Л –±—Л—В—М –≥–Њ–ї–Њ–љ–Њ–Љ–љ—Л–Љ–Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Н–љ—В—А–Њ–њ–Є—П –≤ –љ–Є—Е –љ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–∞, –≥–Њ–≤–Њ—А–Є—В—М –Њ –µ–µ –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є–Є –±–µ—Б—Б–Љ—Л—Б–ї–µ–љ–љ–Њ. –Т –Ї–Њ—Б–Љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ —Н—В–Њ –Љ–Њ–ґ–µ—В –Њ–Ј–љ–∞—З–∞—В—М –ї–Є–±–Њ —Г—Б–Є–ї–µ–љ–Є–µ –і–Є—Б—Б–Є–њ–∞—В–Є–≤–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –≤–Њ –Т—Б–µ–ї–µ–љ–љ–Њ–є, –ї–Є–±–Њ, –љ–∞–Њ–±–Њ—А–Њ—В, –љ–µ–Ї–Є–µ –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –і–Є—Б—Б–Є–њ–∞—Ж–Є–Є.
–Э–Њ –µ—Й–µ –і–Њ —А–µ—И–µ–љ–Є—П –≤–Њ–њ—А–Њ—Б–∞ –Њ –љ–µ–≥–Њ–ї–Њ–љ–Њ–Љ–љ–Њ—Б—В–Є –њ—Д–∞—Д—Д–Њ–≤—Л—Е —Д–Њ—А–Љ –≤ –Ю–Ґ–Ю –≤ —А–∞–Љ–Ї–∞—Е —А–∞—Б—И–Є—А–µ–љ–љ–Њ–є –љ–µ–Њ–±—А–∞—В–Є–Љ–Њ–є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є, –≤ –Ї–Њ—В–Њ—А–Њ–є –љ–µ—В –ї–Њ–Ї–∞–ї—М–љ–Њ–≥–Њ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П, –Љ–Њ–ґ–љ–Њ –≥–Њ–≤–Њ—А–Є—В—М –Њ–± –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П—Е 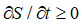 –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П, –µ—Б–ї–Є –Є —В–Њ–ї—М–Ї–Њ –µ—Б–ї–Є –љ–µ –љ–∞—А—Г—И–∞–µ—В—Б—П —Н–љ–µ—А–≥–Њ–і–Њ–Љ–Є–љ–∞–љ—В–љ–Њ—Б—В—М [11]. –Ю–і–љ–∞–Ї–Њ –Љ—Л –Ј–љ–∞–µ–Љ, —З—В–Њ –љ–∞—А—Г—И–µ–љ–Є–µ —Н–љ–µ—А–≥–Њ–і–Њ–Љ–Є–љ–∞–љ—В–љ–Њ—Б—В–Є –≤ –њ–Њ–ї–µ–≤—Л—Е –Љ–Њ–і–µ–ї—П—Е вАФ –љ–µ —А–µ–і–Ї–Њ—Б—В—М [12]. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Г—З–µ—В –≤–∞–Ї—Г—Г–Љ–љ—Л—Е –њ–Њ–њ—А–∞–≤–Њ–Ї –Ј–∞—Б—В–∞–≤–ї—П–µ—В –њ–µ—А–µ–Њ—Б–Љ—Л—Б–ї–Є—В—М –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–µ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ –Ј–∞–Ї–Њ–љ–∞ —Б–Њ—Е—А–∞–љ–µ–љ–Є—П.
–≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П, –µ—Б–ї–Є –Є —В–Њ–ї—М–Ї–Њ –µ—Б–ї–Є –љ–µ –љ–∞—А—Г—И–∞–µ—В—Б—П —Н–љ–µ—А–≥–Њ–і–Њ–Љ–Є–љ–∞–љ—В–љ–Њ—Б—В—М [11]. –Ю–і–љ–∞–Ї–Њ –Љ—Л –Ј–љ–∞–µ–Љ, —З—В–Њ –љ–∞—А—Г—И–µ–љ–Є–µ —Н–љ–µ—А–≥–Њ–і–Њ–Љ–Є–љ–∞–љ—В–љ–Њ—Б—В–Є –≤ –њ–Њ–ї–µ–≤—Л—Е –Љ–Њ–і–µ–ї—П—Е вАФ –љ–µ —А–µ–і–Ї–Њ—Б—В—М [12]. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Г—З–µ—В –≤–∞–Ї—Г—Г–Љ–љ—Л—Е –њ–Њ–њ—А–∞–≤–Њ–Ї –Ј–∞—Б—В–∞–≤–ї—П–µ—В –њ–µ—А–µ–Њ—Б–Љ—Л—Б–ї–Є—В—М –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–µ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ –Ј–∞–Ї–Њ–љ–∞ —Б–Њ—Е—А–∞–љ–µ–љ–Є—П.
2. –•–Њ—В—П, –Ї–∞–Ї —Г–Ї–∞–Ј—Л–≤–∞–ї–Њ—Б—М, —А–∞–Ј–ї–Є—З–љ—Л–µ –∞–≤—В–Њ—А—Л –њ—А–Є–і–µ—А–ґ–Є–≤–∞—О—В—Б—П —А–∞–Ј–љ—Л—Е –≤–Ј–≥–ї—П–і–Њ–≤ –љ–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л, —Б–≤—П–Ј–∞–љ–љ–Њ–є —Б –і–≤–Є–ґ—Г—Й–Є–Љ—Б—П —В–µ–ї–Њ–Љ [13], –µ—Б–ї–Є –≤–≤–µ—Б—В–Є –ї–Њ—А–µ–љ—Ж-–Є–љ–≤–∞—А–Є–∞–љ—В–љ—Г—О —В–µ–Љ–њ–µ—А–∞—В—Г—А—Г, –Љ–Њ–ґ–љ–Њ –њ—А–Є–і–∞—В—М –≤—В–Њ—А–Њ–Љ—Г –љ–∞—З–∞–ї—Г —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є 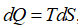 , –≥–і–µ —Н–љ—В—А–Њ–њ–Є—П S вАФ –Є–љ–≤–∞—А–Є–∞–љ—В, —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї—Г—О —Д–Њ—А–Љ—Г. –Т–≤–µ—Б—В–Є
, –≥–і–µ —Н–љ—В—А–Њ–њ–Є—П S вАФ –Є–љ–≤–∞—А–Є–∞–љ—В, —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї—Г—О —Д–Њ—А–Љ—Г. –Т–≤–µ—Б—В–Є
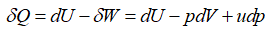
–У–і–µ U вАФ –≤–љ—Г—В—А–µ–љ–љ—П—П —Н–љ–µ—А–≥–Є—П, W вАФ —А–∞–±–Њ—В–∞ –≤–љ–µ—И–љ–Є—Е —Б–Є–ї, —А вАФ –і–∞–≤–ї–µ–љ–Є–µ, V вАФ –Њ–±—К–µ–Љ.
–Т –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –≤—Е–Њ–і—П—В –Њ–±–Њ–±—Й–µ–љ–љ—Л–µ –≤–љ–µ—И–љ–Є–µ —Б–Є–ї—Л –Є —Е–Є–Љ–Є—З–µ—Б–Ї–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї 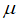 –Є –Є–Ј–Љ–µ–љ–µ–љ–Є–µ —З–Є—Б–ї–∞ —З–∞—Б—В–Є—Ж dN. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≥—А–∞–љ–Є—Ж—Л –≤–ї–Є—П—О—В –љ–∞ —Б–Є—Б—В–µ–Љ—Г, –љ–∞–Є–±–Њ–ї–µ–µ –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ–є –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є —П–≤–ї—П–µ—В—Б—П –і–∞–≤–ї–µ–љ–Є–µ p, –≤ —Б–≤—П–Ј–Є —Б —З–µ–Љ –≤ –Ї–∞—З–µ—Б—В–≤–µ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Г–і–Њ–±–љ–Њ –±—А–∞—В—М —Н–љ—В–∞–ї—М–њ–Є—О. –Ф–ї—П —В–∞–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л ¬Ђ–Њ–±—Л—З–љ–∞—П¬ї —Н–љ—В–∞–ї—М–њ–Є—П –Є –Є–Љ–њ—Г–ї—М—Б —Б–Є—Б—В–µ–Љ—Л
–Є –Є–Ј–Љ–µ–љ–µ–љ–Є–µ —З–Є—Б–ї–∞ —З–∞—Б—В–Є—Ж dN. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≥—А–∞–љ–Є—Ж—Л –≤–ї–Є—П—О—В –љ–∞ —Б–Є—Б—В–µ–Љ—Г, –љ–∞–Є–±–Њ–ї–µ–µ –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ–є –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є —П–≤–ї—П–µ—В—Б—П –і–∞–≤–ї–µ–љ–Є–µ p, –≤ —Б–≤—П–Ј–Є —Б —З–µ–Љ –≤ –Ї–∞—З–µ—Б—В–≤–µ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Г–і–Њ–±–љ–Њ –±—А–∞—В—М —Н–љ—В–∞–ї—М–њ–Є—О. –Ф–ї—П —В–∞–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л ¬Ђ–Њ–±—Л—З–љ–∞—П¬ї —Н–љ—В–∞–ї—М–њ–Є—П –Є –Є–Љ–њ—Г–ї—М—Б —Б–Є—Б—В–µ–Љ—Л 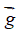 –Њ–±—А–∞–Ј—Г—О—В
–Њ–±—А–∞–Ј—Г—О—В
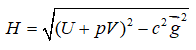
–Т–≤–µ–і–µ–Љ
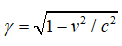
–Ю—Б–љ–Њ–≤–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –Ј–∞–њ–Є—Б—Л–≤–∞–µ—В—Б—П (—Б–Љ. [14]) —З–µ—А–µ–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ–є —Н–љ—В–∞–ї—М–њ–Є–Є —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
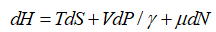
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ–±—К–µ–Љ –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П –Ї–∞–Ї 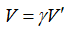 , –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є—П –Ъ–ї–∞–њ–µ–є—А–Њ–љ–∞-–Ь–µ–љ–і–µ–ї–µ–µ–≤–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –і–∞–≤–ї–µ–љ–Є–µ –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
, –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є—П –Ъ–ї–∞–њ–µ–є—А–Њ–љ–∞-–Ь–µ–љ–і–µ–ї–µ–µ–≤–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –і–∞–≤–ї–µ–љ–Є–µ –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: 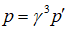 . –Ґ–Њ–≥–і–∞ –Є–Ј
. –Ґ–Њ–≥–і–∞ –Є–Ј 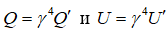 .
.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г dN вАФ –Є–љ–≤–∞—А–Є–∞–љ—В, —В–Њ 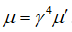 .
.
–§—Г–љ–Ї—Ж–Є—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П
–Ф–ї—П —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Ї–Є —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є—Е –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Є—Е —Г—А–∞–≤–љ–µ–љ–Є–є [15], —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є—Е —Г—А–∞–≤–љ–µ–љ–Є–є —Б–њ–ї–Њ—И–љ–Њ–є —Б—А–µ–і—Л —Б —В–µ–Љ–њ–µ—А–∞—В—Г—А–Њ–є [16], –≤ –њ–Њ–і—Е–Њ–і–µ –У–Є–±–±–Њ–љ—Б–∞ –Є –•–Њ–Ї–Є–љ–≥–∞ –і–ї—П –Њ–њ–Є—Б–∞–љ–Є—П —З–µ—А–љ—Л—Е –і—Л—А –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–є –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Є–є –∞–љ—Б–∞–Љ–±–ї—М –У–Є–±–±—Б–∞.
–Э–Њ –і–µ–ї–Њ –µ—Й–µ –Є –≤ —В–Њ–Љ, —З—В–Њ –≤—В–Њ—А–Њ–є –Ј–∞–Ї–Њ–љ —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є, –Ј–∞–Ї–Њ–љ –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є—П —Н–љ—В—А–Њ–њ–Є–Є, –љ–µ –Љ–µ–љ—П–µ—В—Б—П –≤ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–Љ –њ–Њ–ї–µ, –љ–∞–њ—А–Є–Љ–µ—А, –љ–∞ –Ч–µ–Љ–ї–µ, –њ–Њ—В–Њ–Љ—Г, —З—В–Њ –≤ –µ–≥–Њ –Њ—Б–љ–Њ–≤–µ –ї–µ–ґ–Є—В —Б–Є–Љ–Љ–µ—В—А–Є—П —Н–≤–Ї–ї–Є–і–Њ–≤–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞. –Ч–∞–Ї–Њ–љ—Л —Д–Є–Ј–Є–Ї–Є —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Л –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –≥—А—Г–њ–њ—Л –У–∞–ї–Є–ї–µ—П –≤ –µ–≤–Ї–ї–Є–і–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ, –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Ь–Є–љ–Ї–Њ–≤—Б–Ї–Њ–≥–Њ вАФ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –≥—А—Г–њ–њ—Л –Ы–Њ—А–µ–љ—Ж–∞. –Э–Њ —Б–Є–ї—М–љ–Њ –Є—Б–Ї—А–Є–≤–ї–µ–љ–љ—Л–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ –Њ–њ–Є—Б—Л–≤–∞—О—В—Б—П –Є–љ—Л–Љ–Є –≥—А—Г–њ–њ–∞–Љ–Є —Б–Є–Љ–Љ–µ—В—А–Є–Є, –≥—А—Г–њ–њ–Њ–є –С–Њ–љ–і–Є-–Ь–µ—В—Ж–љ–µ—А–∞-–°–∞–Ї—Б–∞ –Є –і—А. –Ґ–Њ –µ—Б—В—М, —В–µ–Њ—А–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –≤ –Ю–Ґ–Ю вАФ –і—А—Г–≥–∞—П, –≤ –љ–µ–є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –У–∞—Г—Б—Б–∞ (–љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Я–Є—А—Б–Њ–љ–∞ —В–Є–њ–∞ IX), , –Ъ–Њ—И–Є, –§–Є—И–µ—А–∞, –ї–Њ–≥–љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ, –Я—Г–∞—Б—Б–Њ–љ–∞ вАФ –љ–µ —Б–Є–Љ–Љ–µ—В—А–Є—З–љ—Л.
–Т [2, —Б. 112] —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –С–Њ–Ј–µ –Є –§–µ—А–Љ–Є –њ–Њ–ї—Г—З–∞—О—В, –Є—Б—Е–Њ–і—П –Є–Ј –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П —Б —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є–Љ –∞—А–≥—Г–Љ–µ–љ—В–Њ–Љ. –Ю–і–љ–∞–Ї–Њ –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –њ—А–Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П—Е –Ы–Њ—А–µ–љ—Ж–∞, –µ—Б–ї–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л вАФ –≤–і–Њ–ї—М –≤–µ–Ї—В–Њ—А–∞ —Б–Ї–Њ—А–Њ—Б—В–Є —Б–Є—Б—В–µ–Љ—Л –Њ—В—Б—З–µ—В–∞, —Б–Љ–µ—Й–∞–µ—В—Б—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ
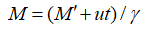
–Є –≤ —Д–Њ—А–Љ—Г–ї–µ –і–ї—П –њ–ї–Њ—В–љ–Њ—Б—В–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є
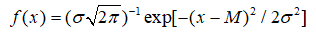
—Г–Љ–µ–љ—М—И–∞–µ—В—Б—П –і–Є—Б–њ–µ—А—Б–Є—П 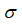 :
:
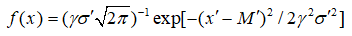
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Б–∞–Љ–∞ –њ–ї–Њ—В–љ–Њ—Б—В—М –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –њ—А–Є –њ–µ—А–µ—Е–Њ–і–µ –≤ –і–≤–Є–ґ—Г—Й—Г—О—Б—П —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П —Б–ї–Њ–ґ–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ.
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П –Є —Д–Њ—А–Љ—Г–ї–∞ –®–µ–љ–љ–Њ–љ–∞ –і–ї—П —Н–љ—В—А–Њ–њ–Є–Є.
–Ч–∞–Ї–ї—О—З–µ–љ–Є–µ.
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Д—Г–љ–Ї—Ж–Є–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –љ–µ –Љ–Њ–≥—Г—В –±—Л—В—М –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ—Л –і–ї—П –Т—Б–µ–ї–µ–љ–љ–Њ–є –Ї–∞–Ї —Ж–µ–ї–Њ–≥–Њ. –°–Є—Б—В–µ–Љ–∞ –љ–∞–є–і–µ–љ–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–Є –Љ–Њ–ґ–µ—В –њ–Њ–Ј–≤–Њ–ї–Є—В—М —Б–і–µ–ї–∞—В—М —И–∞–≥ –Ї –µ–µ –Ї–Њ–≤–∞—А–Є–∞–љ—В–љ–Њ–є —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Ї–µ –і–ї—П –ї–Њ–Ї–∞–ї—М–љ—Л—Е —Б–Є—Б—В–µ–Љ –Є –Ї —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–є –Ї–Њ—А—А–µ–Ї—В–Є—А–Њ–≤–Ї–µ —Б–њ—Г—В–љ–Є–Ї–Њ–≤—Л—Е –Ї–Њ–Љ–Љ—Г–љ–Є–Ї–∞—Ж–Є–є –љ–∞ –≥—А–∞–љ–Є—Ж–∞—Е –°–Њ–ї–љ–µ—З–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л.
–Ы–Є—В–µ—А–∞—В—Г—А–∞
- Nicastro F, Kaastra J., Krongold Y. et al. Observations of the missing baryons in the warmвАФhot intergalactic medium // Nature. вАФ 2018. вАФ Vol. 558. вАФ P.
406вАУ409. DOI https://doi.org/10.1038/s41586-018-0204-1 - –У–Њ—А–±—Г–љ–Њ–≤ –Ф. –°., –†—Г–±–∞–Ї–Њ–≤ –Т. –Р. –Т–≤–µ–і–µ–љ–Є–µ –≤ —В–µ–Њ—А–Є—О —А–∞–љ–љ–µ–є –Т—Б–µ–ї–µ–љ–љ–Њ–є. –Ґ–µ–Њ—А–Є—П –≥–Њ—А—П—З–µ–≥–Њ –С–Њ–ї—М—И–Њ–≥–Њ –≤–Ј—А—Л–≤–∞. –Ь.: –Ы–Ъ–Ш, 2008. 552 —Б.
- Palma G., Normale S., Sormani M. C., Peierls R. Counterintuitive effect of gravity on the heat capacity of a metal sphere: re-examination of a well-known problem.
- https://arxiv.org/pdf/1502.01337.pdf
- –Ф–∞–љ—Л–ї—М—З–µ–љ–Ї–Њ –Я. –†–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–∞—П —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ —Б –ї–Њ—А–µ–љ—Ж-–Є–љ–≤–∞—А–Є–∞–љ—В–љ—Л–Љ —Н–Ї—Б—В–µ–љ—Б–Є–≤–љ—Л–Љ –Њ–±—К–µ–Љ–Њ–Љ. –Т–Є–љ–љ–Є—Ж–∞: –У–Э–Я–Я ¬Ђ–У–µ–Њ—Б–Є—Б—В–µ–Љ–∞¬ї, 2006. 8 —Б.
- –Ч–µ–ї—М–і–Њ–≤–Є—З –ѓ. –С., –Э–Њ–≤–Є–Ї–Њ–≤ –Ш. –Ф. –°—В—А–Њ–µ–љ–Є–µ –Є —Н–≤–Њ–ї—О—Ж–Є—П –Т—Б–µ–ї–µ–љ–љ–Њ–є. –Ь.: –Э–∞—Г–Ї–∞, 1975. 736 —Б.
- –§—А–Є–і–Љ–∞–љ –Р. –Т., –•–Њ–њ–µ—А—Б–Ї–Њ–≤ –Р. –Ь. –§–Є–Ј–Є–Ї–∞ –≥–∞–ї–∞–Ї—В–Є—З–µ—Б–Ї–Є—Е –і–Є—Б–Ї–Њ–≤. –Ь.: –§–Є–Ј–Љ–∞—В–ї–Є—В, 2011. 640 —Б.
- –Ъ–∞–ї–ї–µ–љ –У., –У–Њ—А–≤–Є—Ж –Ф–ґ. –†–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–∞—П —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ // –£–§–Э. вАФ 1972. вАФ –Ґ. 107. вАФ –≤—Л–њ. 3. вАФ –°.
489вАУ502 - –Ґ–Њ–ї–Љ–µ–љ –†. –Ю—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В—М, —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –Є –Ї–Њ—Б–Љ–Њ–ї–Њ–≥–Є—П. –Ь.: –Э–∞—Г–Ї–∞, 1974. 520 —Б.
- –Т–Њ—А–Њ–љ—Ж–Њ–≤-–Т–µ–ї—М—П–Љ–Є–љ–Њ–≤ –С. –Р. –Т–љ–µ–≥–∞–ї–∞–Ї—В–Є—З–µ—Б–Ї–∞—П –∞—Б—В—А–Њ–љ–Њ–Љ–Є—П. –Ь.: –Э–∞—Г–Ї–∞, 1978. 480 —Б.
- –У–Є–љ–Ј–±—Г—А–≥ –Т. –Ы. –Ґ–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–∞—П —Д–Є–Ј–Є–Ї–∞ –Є –∞—Б—В—А–Њ—Д–Є–Ј–Є–Ї–∞. –Ь.: –Э–∞—Г–Ї–∞, 1981. 504 —Б.
- –Ц–Њ—Г –Ф., –Ъ–∞—Б–∞—Б-–С–∞—Б–Ї–µ—Б –•., –Ы–µ–±–Њ–љ –Ф–ґ. –†–∞—Б—И–Є—А–µ–љ–љ–∞—П –љ–µ–Њ–±—А–∞—В–Є–Љ–∞—П —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞. M: –Ш–љ—Б—В–Є—В—Г—В –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є, 2006. 528 —Б.
- –Ш—Е–ї–Њ–≤ –С. –Ы. –•–Є–≥–≥—Б–Њ–≤—Б–Ї–Є–є –≤–∞–Ї—Г—Г–Љ –≤ –Ї–∞–ї–Є–±—А–Њ–≤–Њ—З–љ–Њ–є —В–µ–Њ—А–Є–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Є: –Р–≤—В–Њ—А–µ—Д. –і–Є—Б—Б. –Ї–∞–љ–і. —Д–Є–Ј. –Љ–∞—В. –љ–∞—Г–Ї, –Ь., 1988. 14 —Б.
- –®–Љ—Г—В—Ж–µ—А –≠. ¬Ђ–°–Є–Љ–Љ–µ—В—А–Є–Є –Є –Ј–∞–Ї–Њ–љ—Л —Б–Њ—Е—А–∞–љ–µ–љ–Є—П –≤ —Д–Є–Ј–Є–Ї–µ¬ї. –Ь.: –Ь–Є—А, 1974. 159 —Б.
- –С–Њ–ї–≥–∞—А—Б–Ї–Є–є –Р. –Т., –Ь—Г—Е–∞—З–µ–≤ –У. –Р., –©—Г–Ї–Є–љ –Т. –Ъ. –Ґ–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –Є —В–µ–њ–ї–Њ–њ–µ—А–µ–і–∞—З–∞. –Ь.: –Т—Л—Б—И–∞—П —И–Ї–Њ–ї–∞, 1975. 495 —Б.
- –Ф–µ –У—А–Њ–Њ—В –°., –≤–∞–љ –Ы–µ—Г–≤–µ–љ –Т., –≤–∞–љ –Т–µ—А—В –•. ¬Ђ–†–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–∞—П –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–∞—П —В–µ–Њ—А–Є—П¬ї. –Ь.: –Ь–Є—А, 1983. 424 c.
- –І–µ—А–љ—Л–є –Ы. –Ґ. –†–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є–µ –Љ–Њ–і–µ–ї–Є —Б–њ–ї–Њ—И–љ—Л—Е —Б—А–µ–і. –Ь.: –Э–∞—Г–Ї–∞, 1983.









