–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–°–≤–µ–і–µ–љ–Є—П —А–∞–Ј–љ—Л—Е —Д–Њ—А–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е —Б–Є–љ–≥—Г–ї—П—А–љ—Л—Е –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ –і—А—Г–≥ –Ї –і—А—Г–≥—Г
–†—Г–±—А–Є–Ї–∞: –§–Є–Ј–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ9 2015» (—Б–µ–љ—В—П–±—А—М 2015)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 2421
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –°–≤–µ–і–µ–љ–Є—П —А–∞–Ј–љ—Л—Е —Д–Њ—А–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е —Б–Є–љ–≥—Г–ї—П—А–љ—Л—Е –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ –і—А—Г–≥ –Ї –і—А—Г–≥—Г
–Ь–љ–Њ–≥–Є–µ –Ј–∞–і–∞—З–Є –Љ–µ—Е–∞–љ–Є–Ї–Є, —В–µ–Њ—А–Є—П –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є, –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є –Є —В.–і. —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ–Њ —Б –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л–Љ–Є —Б–Є–љ–≥—Г–ї—П—А–љ—Л–Љ–Є –Є–љ—В–µ–≥—А–∞–ї—М–љ—Л–Љ–Є —Г—А–∞–≤–љ–µ–љ–Є—П–Љ–Є [1] –Ш–Ј —З–µ–≥–Њ —Б–ї–µ–і—Г–µ—В –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М —А–∞–Ј—А–∞–±–Њ—В–Ї–Є –њ—А–Є–±–ї–Є–ґ—С–љ–љ—Л—Е –Љ–µ—В–Њ–і—Л –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е —Б–Є–љ–≥—Г–ї—П—А–љ—Л—Е –Є–љ—В–µ–≥—А–∞–ї–Њ–≤. –≠—В–Є–Љ –≤–Њ–њ—А–Њ—Б–Њ–Љ –∞–Ї—В–Є–≤–љ–Њ –Є –њ–ї–Њ–і–Њ—В–≤–Њ—А–љ–Њ –Ј–∞–љ–Є–Љ–∞–ї—Б—П –С.–У.–У–∞–±–і—Г–ї—Е–∞–µ–≤ (—Б–Љ.–љ–∞–њ—А. [2]–Ш –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ –Є–љ—В–µ—А–µ—Б–µ–љ –≤–Њ–њ—А–Њ—Б –Њ —В–Њ–Љ, –Ї–∞–Ї–∞—П —Б—Г—Й–µ—Б—В–≤—Г–µ—В —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —А–∞–Ј–љ—Л–Љ–Є —Д–Њ—А–Љ–∞–Љ–Є —Б–Є–љ–≥—Г–ї—П—А–љ—Л—Е –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ —В–∞–Ї–Є—Е –Ї–∞–Ї, –љ–∞–њ—А–Є–Љ–µ—А, –Є–љ—В–µ–≥—А–∞–ї—Л —Б —П–і—А–∞–Љ–Є —В–Є–њ–∞ –Ъ–Њ—И–Є, —В–Є–њ–∞ –У–Є–ї—М–±–µ—А—В–∞ –Є —В–Є–њ–∞
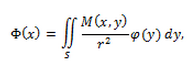
–≥–і–µ –Є - –≤–µ–Ї—В–Њ—А —Д—Г–љ–Ї—Ж–Є–Є, –∞ –љ–µ–Ї–Њ—В–Њ—А–∞—П –Љ–∞—В—А–Є—Ж–∞, –µ—Б–ї–Є , —В–Њ
—Н—В–Њ—В –Є–љ—В–µ–≥—А–∞–ї —П–≤–ї—П–µ—В—Б—П —Б–Є–љ–≥—Г–ї—П—А–љ—Л–Љ.
–° —Н—В–Њ–є —Ж–µ–ї—М—О –≤ —Н—В–Њ–є —А–∞–±–Њ—В–µ –Љ—Л –њ—Л—В–∞–ї–Є—Б—М –Є–Ј—Г—З–Є—В—М —Н—В–Њ—В –≤–Њ–њ—А–Њ—Б –љ–∞ –њ—А–Є–Љ–µ—А–µ —Б–ї–µ–і—Г—О—Й–µ–≥–Њ –Є–љ—В–µ–≥—А–∞–ї–∞.
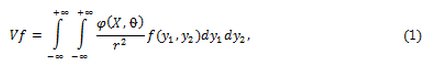
–≥–і–µ
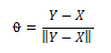
–Х—Б–ї–Є
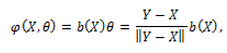
—В–Њ –Є–љ—В–µ–≥—А–∞–ї (1) –њ—А–Є–Љ–µ—В –≤–Є–і:
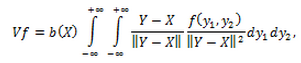
–Є
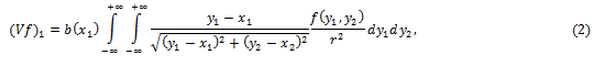
(2)
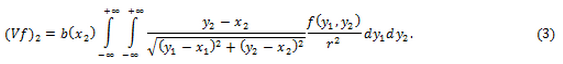
(3)
–Т –њ–Њ—Б–ї–µ–і–љ–Є—Е –Є–љ—В–µ–≥—А–∞–ї–∞—Е –њ—А–Є–≤–µ–і–µ–Љ –Ј–∞–Љ–µ–љ—Г
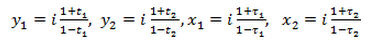
–њ–Њ—Б–ї–µ —З–µ–≥–Њ –Є–Љ–µ–µ–Љ
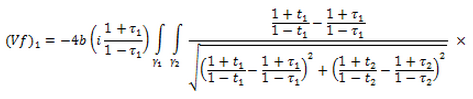
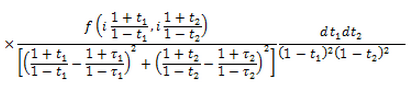
–Є–ї–Є
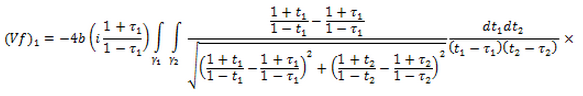
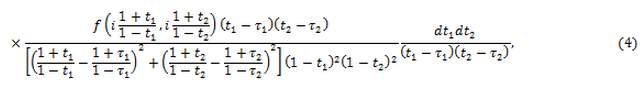
–≥–і–µ - –µ–і–Є–љ–Є—З–љ—Л–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В–µ–њ–µ—А—М –≤–µ–ї–Є—З–Є–љ—Л
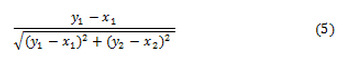

–Є–Ј –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ—Л—Е –≤—Л—А–∞–ґ–µ–љ–Є–є (2) –Є (3).
–Ю–љ–Є —П–≤–ї—П—О—В—Б—П –Њ–≥—А–∞–љ–Є—З–µ–љ–љ—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є, —В–Њ –µ—Б—В—М –Љ–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ
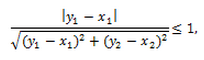
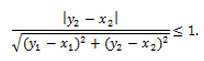
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –µ—Б–ї–Є –Њ–і–љ–Є–Љ –Є —В–µ–Љ –ґ–µ –Ј–∞–Ї–Њ–љ–Њ–Љ –Є , —В–Њ (5) –Є (6) —Б—В—А–µ–Љ—П—В—Б—П –Ї –Њ–і–љ–Њ–Љ—Г –Є —В–Њ–Љ—Г –ґ–µ –њ—А–µ–і–µ–ї—Г .
–Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–µ —А–∞—Б—Б—Г–ґ–і–µ–љ–Є—П –Є–Љ–µ—О—В –Љ–µ—Б—В–∞ –Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Б–ї–µ–і—Г—О—Й–Є—Е –≤–µ–ї–Є—З–Є–љ:
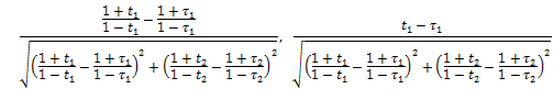
–Є
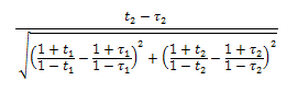
–Т–≤–µ–і—П –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П
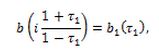
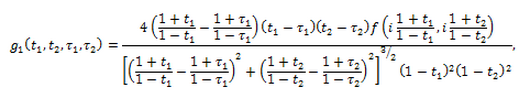
–Є–Ј (4) –Є–Љ–µ–µ–Љ
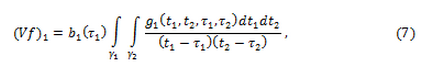
–Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –њ—Г—В–µ–Љ –њ–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ
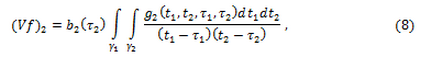
–≥–і–µ
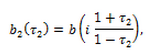
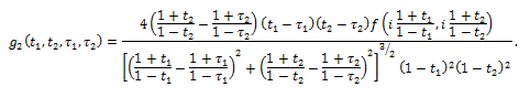
–Ґ–∞–Ї–Є–Љ –ґ–µ –Њ–±—А–∞–Ј–Њ–Љ –Љ–Њ–ґ–љ–Њ —Г—Б—В–∞–љ–Њ–≤–Є—В—М —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г –Є–љ—В–µ–≥—А–∞–ї–∞–Љ–Є –≤–Є–і–∞ (7) –Є (8) –Є —Б–Є–љ–≥—Г–ї—П—А–љ—Л–Љ–Є –Є–љ—В–µ–≥—А–∞–ї–∞–Љ–Є —Б —П–і—А–Њ–Љ –У–Є–ї—М–±–µ—А—В–∞.
–Ы–Є—В–µ—А–∞—В—Г—А–∞:
- –Э.–Ш.–Ь—Г—Б—Е–µ–ї–Є—И–≤–Є–ї–Є. –°–Є–љ–≥—Г–ї—П—А–љ—Л–µ –Є–љ—В–µ–≥—А–∞–ї—М–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П. –Ь., –§–Є–Ј–Љ–∞—В–≥–Є–Ј,1968.
- –С.–У.–У–∞–±–і—Г–ї—Е–∞–µ–≤. –Ъ—Г–±–∞—В—Г—А–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л –і–ї—П –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е —Б–Є–љ–≥—Г–ї—П—А–љ—Л—Е –Є–љ—В–µ–≥—А–∞–ї–Њ–≤. –Ш–Ј–≤. –Т—Г–Ј–Њ–≤, –Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞, 1975, вДЦ4.









