Схема шифрования RSA и её программная реализация

Аннотация

Информация — это одна из самых ценных вещей в современной жизни. Появление глобальных компьютерных сетей сделало простым получение доступа к информации для людей и для организаций. А так же, доступ к личной информации при её передаче получают злоумышленники.

Чтобы обеспечить безопасность личных данных при передаче, необходимо зашифровывать информацию.

Шифрование — это метод защиты любой информации от неавторизованных лиц, с предоставлением, в это же время, авторизованным пользователям доступа к ней.

В данной статье я рассмотрю метод шифрования RSA и метод дополнительного шифрования OAEP, напишу его программную реализацию и сымитирую атаки на RSA.

Ключевые слова: шифр, C++, безопасность, RSA, OAEP.

RSA— криптографический алгоритм с открытым ключом, разработан учёными Ривестом, Шамиром и Адлеманом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Криптографическая система с открытым ключом — система шифрования, при которой открытый ключ передаётся по незащищенному каналу и используется для проверки электронных подписей и для шифрования сообщения. Для генерации электронной подписи и расшифровки сообщений используется закрытый ключ.

Криптографические системы с открытым ключом используют односторонние функции, обладающие свойствами:

· Если известно x, то вычислить f(x) просто.

· Если известно y=f(x), то для вычисления x нет простого пути.

Алгоритм RSA:

1. Создание открытого и закрытого ключа.

1. Выбирается два простых числа u и v.

2. Вычисляется произведение p=u*v.

3. Вычисляется функция Эйлера φ(p)=(u-1)(v-1)

4. Выбираем открытую экспоненту e (1<e< φ(p))

5. Вычисляем закрытую экспоненту d, где (d*e) mod φ(p) =1

6. Получаем открытый ключ (e, p) и закрытый ключ (d, p).

2. Шифрование и дешифрование.

Посмотрим модель шифрования и дешифрования сообщения на конкретном примере. Пусть Алиса хочет послать Бобу сообщение h.

У Алисы есть открытый ключ Боба. А Боб владеет своим закрытым ключом.

w=G(h)= h^e mod p h=Q(w)=w^d mod p

Безопасность схемы шифрования RSA:

Я написала программу на языке высокого уровня С++, где каждый символ кодируется на основании таблицы ASCII, и затем осуществляется алгоритм RSA.

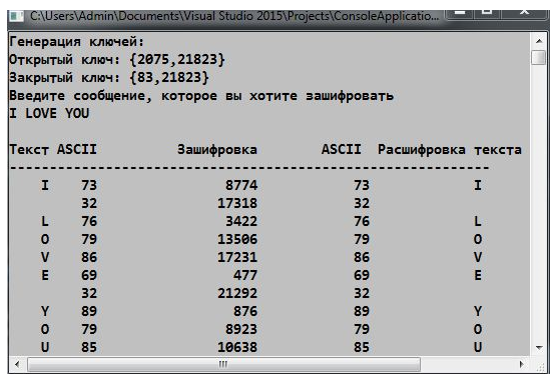
Например, берем символ I, по таблице ASCII его код равен 73. Генерация ключей такая же, как и в примере написанной программы.

w=G(h)= h^e mod p = 73²⁰⁷⁵ mod 21823=8774; (посчитано на инженерном стандартном калькуляторе в операционной системе Windows)

h=Q(w)=w^d mod p = 8774⁸³ mod 21823 = 73 = I

Надёжность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел (v и u). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля на простые сомножители v и u. Если число является произведением двух очень больших простых чисел, что его очень трудно разложить на множители.

Некоторые атаки на RSA.

1. Разложение на множители.

Реализуется на подборе простых чисел u, v, для надёжности числа должны быть большими.

2. Выборка шифрованного текста.

Пусть Ева перехватывает сообщение w от Алисы к Бобу w=z^e (mod n), где z- открытый текст, е — открытый ключ; Ева выбирает число r, r<n и вычисляет с помощью открытого ключа x=r^e (mod n) ,y= x*c (mod n)

Ева передает Y бобу для дешифрования и получает g = y^d mod n. Ева может легко найти z

g= y^d mod n=(w*x^e)^d mod n = (w^d*x^ed)mod n = (w^d*x) mod n =(z*x)mod n
z= (z*x) mod n -> z=w*x^-1 mod n
3. Исходный текст.

Криптосистема RSA обладает низкой криптостойкостью при малой экспоненте на коротком сообщении. Действительно, при c = m^e < n открытый текст m может быть восстановлен по шифротексту © при помощи процедуры извлечения корня. Однако меры противодействия также очевидны, — либо открытый ключ e должен быть достаточно большим, либо открытый текст не должен быть коротким. Выбор малого e обусловлен соображениями вычислительной эффективности шифрования и проверки подписи.

Это показывает, что применение на практике шифрования RSA обладает низкой криптостойкостью, поэтому пользуются схемой дополнительного шифрования OAEP.

Оптимальное асимметричное дополнение шифрования (OAEP — Optimal Assimetric Encryption Padding) — схема дополнения, обычно используемая совместно с какой-либо односторонней функцией с потайным входом (например RSA или функции Рабина) для повышения криптостойкости последней.

Шифрование. Ниже показаны шаги процесса шифрования.

1. Дополняем сообщение, чтобы сделать его w -битовым. Обозначим его W.
2. Выбираем случайное число s (одноразовое число) из k бит.
3. Используем общедоступную одностороннюю функцию G, которая принимает целое s -битовое число, и создает w -разрядное целое число (w — размера W, и s <w ).
4. Применяет маску, G (s), чтобы создать первую часть исходного текста P₁=W+G(s) является замаскированным сообщением.
5. Создаём вторую часть исходного текста P₂ = H(P₁) + s. Функция H — другая общедоступная функция, которая принимает w -битовые входные сообщения и создает k -битовые выходные сообщения.
6. Cоздаём C = P^e = (P₁ || P₂) ^e и передаём C.

Дешифрование. Следующие шаги показывают процесс дешифрования:

1. Создаём P = C^d = (P₁ || P₂).
2. Обновляем значение s, используя H(P₁) + P₂= H(P₁) + H(P₂) + s =s.
3. Применяет G(s) + P = G(s) + G(s) + W=W , чтобы обновить значение дополненного сообщения.
4. После удаления дополнения W, находим первоначальное сообщение.

Алгоритм OAEP применяется для предварительной обработки сообщения перед использованием RSA. Сначала сообщение дополняется до фиксированной длины с помощью OAEP, затем шифруется с помощью RSA.

Литература:

1. Венбо Мао. Современная криптография. Теория и практика = Modern Cryptography: Theory and Practice. — М.: Вильямс, 2005.
2. Нильс Фергюсон, Брюс Шнайер. Практическая криптография = Practical Cryptography: Designing and Implementing Secure Cryptographic Systems. — М.: Диалектика, 2004.
3. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002.