Построение модели скрытых террористических сетей

Ключевые слова: СОЦИАЛЬНЫЕ СЕТИ, СКРЫТЫЕ СЕТИ, ПРОЦЕСС ОБРАБОТКИ ДАННЫХ.

Аннотация

Анализ социальных сетей был использован для понимания групп людей и того, как они действуют. Большая часть литературы в социальных сетях имело дело с открытыми организациями с легко различимой структурой сети. Эта статья рассматривает возможность использования свойственных для социальных сетей структур, чтобы делать прогнозы сетей, используя ограниченную и недостающую информацию. Модель основана на эмпирических данных сети, проявляющих структурные свойства триад смыкания и смежности. Триада смыкания показывает, что если человек i имеет диаду с человеком j и человек j имеет диаду с человеком k, то высока вероятность того, что человек i и k имеют диаду. Смежность является следствием триады смыкания, обозначающая, что если человек i имеет диаду с человеком j, то наиболее вероятно, что человек iимеет диаду с человеком k. Модель эксплуатирует эти свойства, используя логическую модель вывода для обновления смежных диад, ссылаясь на основную. Модель проверялась на нескольких сетях, чтобы понимать и различать её поведение. Статья показывает, что если модель построена с тщательным рассмотрением прогнозируемой сети, то это может помочь в принятии более эффективных решений в отношении неопределенного организационного феномена. Однако модель выполняется относительно плохо, если имеется непропорционально большое количество информации с поддержкой или без поддержки диад, и/или, если основные диады хорошо проинформированы. Метод применялся на примере скрытой сети и был расширен для эпидемиологических сетей и повышения производительности в организациях, работающих в условиях стресса. Статья открывает новые возможности в развитии моделей, предназначенных делать сетевые прогнозы и использовать эти предсказания для принятия более обоснованных решений.

Построение модели

Область проблемы будет определять отношение интересов. В большинстве реальных ситуаций могут наблюдаться только образцы ситуаций взаимодействия между людьми. В зависимости от типа взаимодействия, зная, что i и j взаимодействовали, определятся наши догадки о вероятности отношения интересов, существующих между людьми. Но что, если вывод, сделанный об этих отношениях, можно сделать и об отношении других в сети?

В целях иллюстрации и способствованию развитию модели, мы сфокусируемся на данных одной социальной сети, Бернард и Килворт (Bernard и Killworth) 1979 наблюдали взаимодействия между 58-ю студентами в братстве в университете Западной Вирджинии. Из-за размера этого набора данных, так и не удалось разработать надежную модель логического вывода на основе свойств триад смыкания. Вместо этого модель основана на свойствах смежности, найденных в данных. На рисунке 1 показано отношение между взаимодействиями на основной диаде и ожидаемым числом взаимодействий на смежной диаде. При повышении числа взаимодействий на основной диаде, тоже ожидается и на смежной диаде.

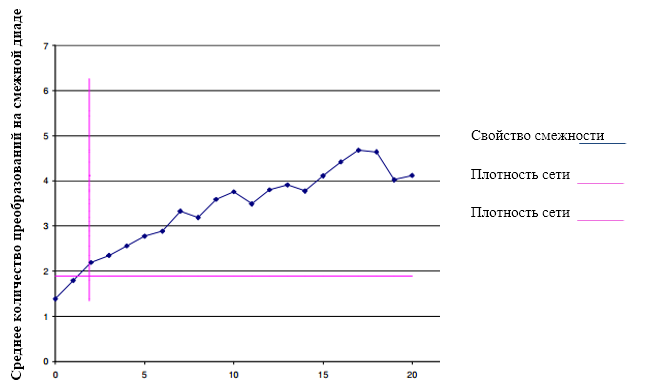
Рисунок 1. Иллюстрация свойств смежности, используя данные братства Бернарда и Килворта

Преобразование данных

Для того, чтобы построить модель диадных зависимостей, данные сети о «количествах взаимодействий» должны быть преобразованы в вероятности того, что отношения интересов существуют между любой парой людей. Чтобы сделать этого, требуется тщательное определение того, что представляет собой отношение интересов. Должно быть рассмотрено две важных вещи.

1. Число необходимых взаимодействий для определения, когда существуют отношений интересов.

2. Незначительное увеличение каждого дополнительного взаимодействия к вероятности существующих отношений интересов.

Мы так же должны установить функциональную форму, которая связывает дополнительные взаимодействия с вероятностью отношения интересов. В данной работе мы исходим из вогнутой функции (предельное уменьшение значения). Используется стандартная экспоненциальная функция:

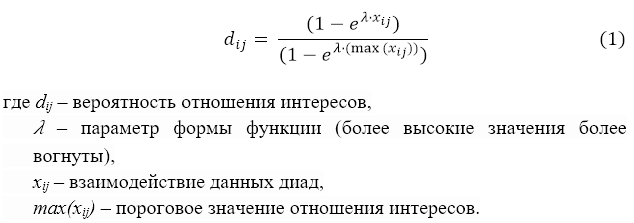
Построение модели диадной зависимости

Зависимость между диадами можно показать путем построения вероятности смежных диад в сравнении с основными диадами для всех диадных пар. На рисунке 2 показаны процентные контуры для преобразованных данных о братстве. Обратите внимание, что процентные контуры, как правило увеличиваются с вероятностью.

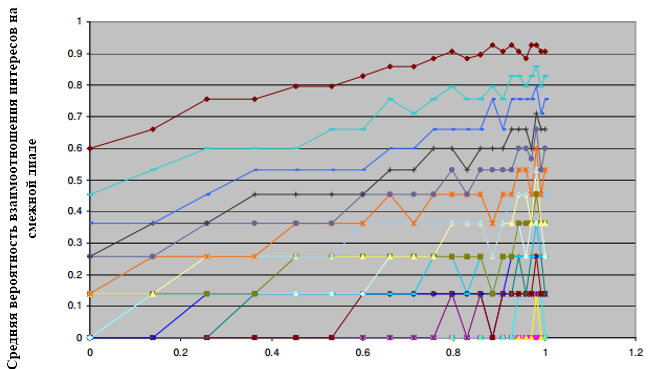
Подходящие линии через эти данные и сглаживание параметров могут ясно показать зависимость между диадическими вероятностями в братстве. Для этого приложения, отношения, показанные на графиках были смоделированы с помощью нейронной сети.(Фримэн и Скапура (Freeman and Skapura),1991) Нейронная сеть состоит из 9-ти узлов и 3-х слоев.

Выводы

Результаты моделирования показывают, что работа моделей вывода смешана. Моделирование было выполнено с части данных, из которых была построена модель, это означает, что результаты показаны в лучшем случае. Модели действительно выступают относительно хорошо, когда есть пропорциональное количество информации, поддерживающих и не поддерживающих существование диады.

Список используемых источников

1. Skvoretz, J., 1990, «Biased Net Theory: Approximations, Simulations, and Observations,» Social Networks, 12, 217-238.
2. Sparrow, M.K., 1991, «The Application of Network Analysis to Criminal Intelligence: An Assessment of the Prospects,» Social Networks, 13, 251-274.
3. McPherson, J.M., P.A. Popielarz, and S. Drobnic, 1992, «Social Networks and Organizational Dynamics,» American Sociological Review, 57, 153-170.
4. Krebs, V., 2001, «Mapping Networks of Terrorist Cells,» Connections, 24(3), 43-52.
5. Krackhardt, D., 1987, «Cognitive Social Structures,» Social Networks, 9, 104-134.