–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ю –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ –љ—Г–ї–µ–є —Г—А–∞–≤–љ–µ–љ–Є—П y^IV¬±ќ≥q(t)=0
–†—Г–±—А–Є–Ї–∞: –§–Є–Ј–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: « –Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ10 2016» (–Њ–Ї—В—П–±—А—М)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 2164
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ю –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ –љ—Г–ї–µ–є —Г—А–∞–≤–љ–µ–љ–Є—П y^IV¬±ќ≥q(t)=0
–≠–≥–∞–Љ–±–µ—А–і–Є–µ–≤–∞ –С–∞—А–љ–∞—Е–Њ–љ –У—Г–ї—П–Љ–і–ґ–∞–љ–Њ–≤–љ–∞
–Я—А–µ–њ–Њ–і–∞–≤–∞—В–µ–ї—М –Ї–∞—Д–µ–і—А—Л ¬Ђ–Т—Л—Б—И–µ–є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є
–Є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Њ–љ–љ—Л—Е —В–µ—Е–љ–Њ–ї–Њ–≥–Є–є¬ї
–Р–љ–і–Є–ґ–∞–љ—Б–Ї–Є–є —Б–µ–ї—М—Б–Ї–Њ—Е–Њ–Ј—П–є—Б—В–≤–µ–љ–љ—Л–є –Є–љ—Б—В–Є—В—Г—В
E-mail: serius-bexruz@mail.ru
–Я—Г—Б—В—М q(t)- –Ї—Г—Б–Њ—З–љ–Њ-–љ–µ–њ—А–µ—А—Л–≤–љ–∞—П, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–∞—П, –љ–µ–Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –љ–∞ –Њ—В—А–µ–Ј–Ї–µ aвЙ§tвЙ§b. –І–µ—А–µ–Ј N(ќ≥) –Њ–±–Њ–Ј–љ–∞—З–Є–Љ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –і–≤—Г–Ї—А–∞—В–љ—Л—Е –љ—Г–ї–µ–є –љ–µ—В—А–Є–≤–Є–∞–ї—М–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П y(t;ќ≥) —Г—А–∞–≤–љ–µ–љ–Є—П
–љ–∞ –Њ—В—А–µ–Ј–Ї–µ aвЙ§tвЙ§b, —В–Њ –µ—Б—В—М ![]()
–°–њ—А–∞–≤–µ–і–ї–Є–≤–∞ —Б–ї–µ–і—Г—О—Й–∞—П —В–µ–Њ—А–µ–Љ–∞:
–Ґ–µ–Њ—А–µ–Љ–∞: –Ш–Љ–µ–µ—В –Љ–µ—Б—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ:
–≥–і–µ ѕЙ - –њ–µ—А–≤—Л–є –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л–є –Ї–Њ—А–µ–љ—М —Г—А–∞–≤–љ–µ–љ–Є—П chѕЙcosѕЙ=1.
–Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ:
–∞) –њ—Г—Б—В—М ќ≥q(t)=k4=const,aвЙ§tвЙ§b. –Ґ–Њ–≥–і–∞ –љ–µ—В—А—Г–і–љ–Њ –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ (1) –Є–Љ–µ–µ—В –Њ–±—Й–µ–µ —А–µ—И–µ–љ–Є–µ –≤–Є–і–∞:
![]()
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј ![]() - –і–≤–µ —Б–Њ—Б–µ–і–љ–Є–µ –і–≤—Г–Ї—А–∞—В–љ—Л–µ –љ—Г–ї–Є —А–µ—И–µ–љ–Є—П y(t), —В.–µ.
- –і–≤–µ —Б–Њ—Б–µ–і–љ–Є–µ –і–≤—Г–Ї—А–∞—В–љ—Л–µ –љ—Г–ї–Є —А–µ—И–µ–љ–Є—П y(t), —В.–µ.
![]()
–Ф–∞–ї–µ–µ –њ–Њ–ї–Њ–ґ–Є–≤ ![]() –њ–Њ–ї—Г—З–Є–Љ, —З—В–Њ
–њ–Њ–ї—Г—З–Є–Љ, —З—В–Њ ![]() , —В.–µ.
, —В.–µ.
![]()
–Я—Г—Б—В—М ѕЙ - –њ–µ—А–≤—Л–є –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л–є –Ї–Њ—А–µ–љ—М —Г—А–∞–≤–љ–µ–љ–Є—П ![]() , –≥–і–µ
, –≥–і–µ ![]() .
.
–Ю—В—Б—О–і–∞ –Ј–∞–Ї–ї—О—З–∞–µ–Љ, —З—В–Њ ![]() , —В.–µ.
, —В.–µ. ![]() .
.
–Ґ–Њ–≥–і–∞ —З–Є—Б–ї–Њ –љ—Г–ї–µ–є ![]() —Г—А–∞–≤–љ–µ–љ–Є—П (1) –љ–∞ –Њ—В—А–µ–Ј–Ї–µ
—Г—А–∞–≤–љ–µ–љ–Є—П (1) –љ–∞ –Њ—В—А–µ–Ј–Ї–µ ![]() —А–∞–≤–љ–Њ
—А–∞–≤–љ–Њ
![]()
–Я–Њ—Н—В–Њ–Љ—Г
![]()
–±) –њ—Г—Б—В—М —В–µ–њ–µ—А—М ![]() - —Б—В—Г–њ–µ–љ—З–∞—В–∞—П —Д—Г–љ–Ї—Ж–Є—П. –Ю—В—А–µ–Ј–Њ–Ї
- —Б—В—Г–њ–µ–љ—З–∞—В–∞—П —Д—Г–љ–Ї—Ж–Є—П. –Ю—В—А–µ–Ј–Њ–Ї ![]() —А–∞–Ј–±–Є—В –љ–∞ –Ї–Њ–љ–µ—З–љ–Њ–µ —З–Є—Б–ї–Њ –Њ—В—А–µ–Ј–Ї–Њ–≤
—А–∞–Ј–±–Є—В –љ–∞ –Ї–Њ–љ–µ—З–љ–Њ–µ —З–Є—Б–ї–Њ –Њ—В—А–µ–Ј–Ї–Њ–≤ ![]() –Є
–Є ![]() . –Я—Г—Б—В—М
. –Я—Г—Б—В—М ![]() —З–Є—Б–ї–Њ –і–≤—Г–Ї—А–∞—В–љ—Л—Е –љ—Г–ї–µ–є —А–µ—И–µ–љ–Є—П
—З–Є—Б–ї–Њ –і–≤—Г–Ї—А–∞—В–љ—Л—Е –љ—Г–ї–µ–є —А–µ—И–µ–љ–Є—П ![]() —Г—А–∞–≤–љ–µ–љ–Є—П (1) –љ–∞ –Њ—В—А–µ–Ј–Ї–µ
—Г—А–∞–≤–љ–µ–љ–Є—П (1) –љ–∞ –Њ—В—А–µ–Ј–Ї–µ ![]() –Ґ–Њ–≥–і–∞ —Б–Њ–≥–ї–∞—Б–љ–Њ –њ—Г–љ–Ї—В—Г –∞) –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
–Ґ–Њ–≥–і–∞ —Б–Њ–≥–ї–∞—Б–љ–Њ –њ—Г–љ–Ї—В—Г –∞) –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
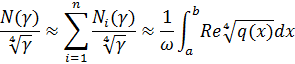
—В.–µ.
—Б) –њ—Г—Б—В—М –љ–∞–Ї–Њ–љ–µ—Ж, ![]() -–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞—П –Ї—Г—Б–Њ—З–љ–Њ-–љ–µ–њ—А–µ—А—Л–≤–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П. –†–∞–Ј–Њ–±—М—С–Љ –Њ—В—А–µ–Ј–Њ–Ї
-–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–∞—П –Ї—Г—Б–Њ—З–љ–Њ-–љ–µ–њ—А–µ—А—Л–≤–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П. –†–∞–Ј–Њ–±—М—С–Љ –Њ—В—А–µ–Ј–Њ–Ї ![]() –љ–∞ n —А–∞–≤–љ—Л—Е —З–∞—Б—В–µ–є
–љ–∞ n —А–∞–≤–љ—Л—Е —З–∞—Б—В–µ–є ![]() –Є –њ–Њ–ї–Њ–ґ–Є–≤ –њ—А–Є
–Є –њ–Њ–ї–Њ–ґ–Є–≤ –њ—А–Є ![]() –Є–Љ–µ–µ–Љ:
–Є–Љ–µ–µ–Љ:
![]() ,
, ![]() ,
, ![]()
–Я—Г—Б—В—М ![]() - —А–µ—И–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П (1) –≤ –Ї–Њ—В–Њ—А–Њ–Љ –≤–Љ–µ—Б—В–Њ
- —А–µ—И–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П (1) –≤ –Ї–Њ—В–Њ—А–Њ–Љ –≤–Љ–µ—Б—В–Њ ![]() —Б—В–Њ–Є—В
—Б—В–Њ–Є—В ![]() –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј ![]() —З–Є—Б–ї–Њ –і–≤—Г–Ї—А–∞—В–љ—Л—Е –љ—Г–ї–µ–є
—З–Є—Б–ї–Њ –і–≤—Г–Ї—А–∞—В–љ—Л—Е –љ—Г–ї–µ–є ![]() –Ї–Њ—А–љ–µ–є –љ–∞
–Ї–Њ—А–љ–µ–є –љ–∞ ![]() . –Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –Њ–њ—А–µ–і–µ–ї–Є–Љ
. –Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –Њ–њ—А–µ–і–µ–ї–Є–Љ ![]() . –Ґ–Њ–≥–і–∞ –≤ —Б–Є–ї—Г —В–µ–Њ—А–µ–Љ—Л —Б—А–∞–≤–љ–µ–љ–Є—П –®—В—Г—А–Љ–∞, –ї–µ–≥–Ї–Њ –Њ–±–љ–∞—А—Г–ґ–Є—В—М, —З—В–Њ
. –Ґ–Њ–≥–і–∞ –≤ —Б–Є–ї—Г —В–µ–Њ—А–µ–Љ—Л —Б—А–∞–≤–љ–µ–љ–Є—П –®—В—Г—А–Љ–∞, –ї–µ–≥–Ї–Њ –Њ–±–љ–∞—А—Г–ґ–Є—В—М, —З—В–Њ
![]()
![]()
–°–Њ–≥–ї–∞—Б–љ–Њ –њ—А–µ–і—Л–і—Г—Й–Є–Љ –њ—Г–љ–Ї—В–∞–Љ –∞) –Є –±) –Є–Љ–µ–µ–Љ:
![]() ,
,
![]()
–Ю—В—Б—О–і–∞ –њ—А–Є ![]() –њ–Њ–ї—Г—З–Є–Љ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ —В–µ–Њ—А–µ–Љ—Л.
–њ–Њ–ї—Г—З–Є–Љ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ —В–µ–Њ—А–µ–Љ—Л.
–Ы–Є—В–µ—А–∞—В—Г—А–∞:
- –Т.–Т.–°—В–µ–њ–∞–љ–Њ–≤. –Ъ—Г—А—Б –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. -–Ь.:–Э–∞—Г–Ї–∞.1959 –≥.
- –Ы.–°.–Я–Њ–љ—В—А—П–≥–Є–љ. –Ю–±—Л–Ї–љ–Њ–≤–µ–љ–љ—Л–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П.-–Ь.:–Э–∞—Г–Ї–∞.1974 –≥.
- –Ѓ.–Э.–С–Є–±–Є–Ї–Њ–≤. –Ю–±—Й–Є–є –Ї—Г—А—Б –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –Ш–Ј–і.–Ы–У–£.,1981 –≥.









