Исследование ФНЧ с применением теории нечетких множеств на различные виды шумов

М.Т. Дусюпова, магистрант кафедры ТОР

Научный консультант Д.А.Титов, доцент ОмГТУ, к.т.н.

г.Томск, ТУСУР, maxo.01@mail.ru

Цель: Исследование сигнала в ФНЧ при различных видах шумов.

Ключевые слова: Фильтр низких частот (ФНЧ); сигнал, шум.

Ранее известный фильтр низких частот [1] был применен для обработки сигналов различных типов.

Алгоритм ФНЧ с применением теории нечетких множеств:

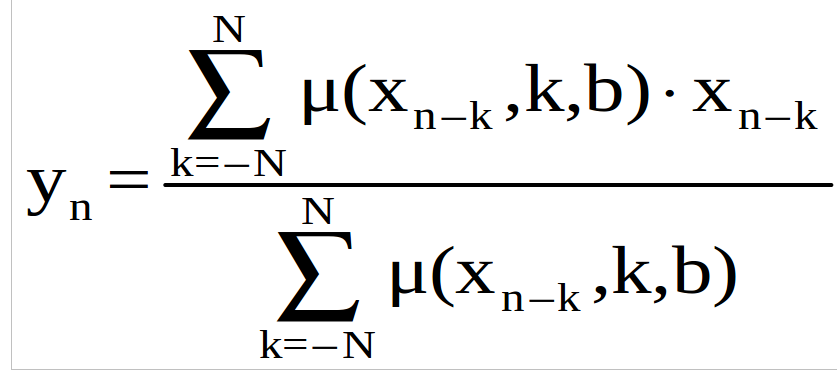где (xn-k) – функция принадлежности разности отсчетов, (хn – хn-k ).

Структурная схема фильтра имеет вид:

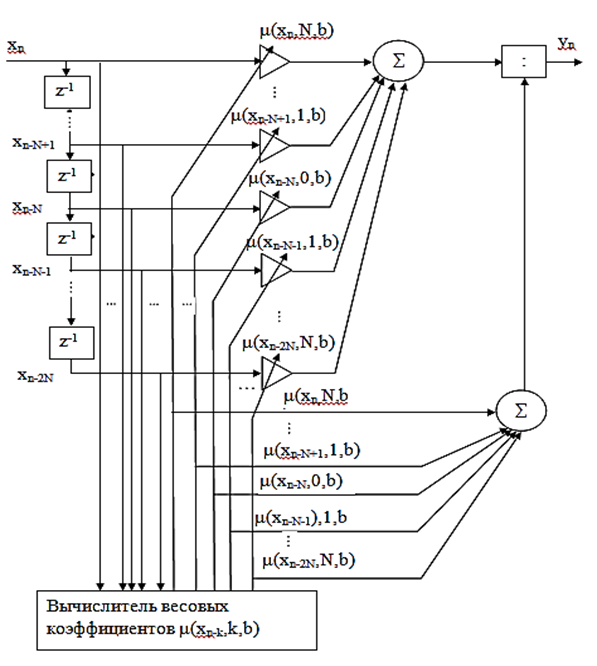
Адаптивный цифровой фильтр с данным алгоритмом обладает следующими характеристиками (при частоте дискретизации сигнала 250 Гц и N=4):

• Тип фильтра: ФНЧ;
• Ширина полосы пропускания, Гц: 7,5 - 30,0;
• Граница полосы задержания, Гц: 17,5 - 35,0;
• Неравномерность в полосе пропускания, дБ: 0,5;
• Затухание в полосе задержания, дБ: не менее 12,0
• Исследование.

В первом случае был взят фрагмент оцифрованной реальной кардиограммы с добавлением белого гауссовского шума, затем сигнал был пропущен через ФНЧ. Результат наложения белого гауссовского шума на фрагмент кардиограммы представлен на рисунке 2.

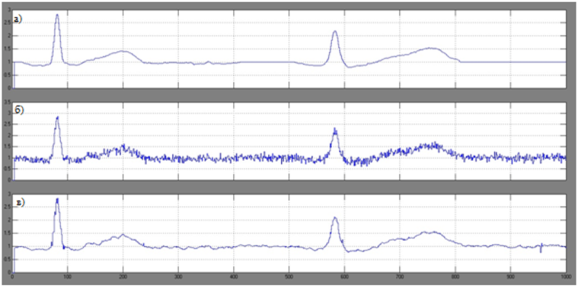Рисунок 2 – Сигнал с наложением белого гауссовского шума

Далее представим результат на выходе ФНЧ с наложением райссовского шума на фрагмент кардиограммы.

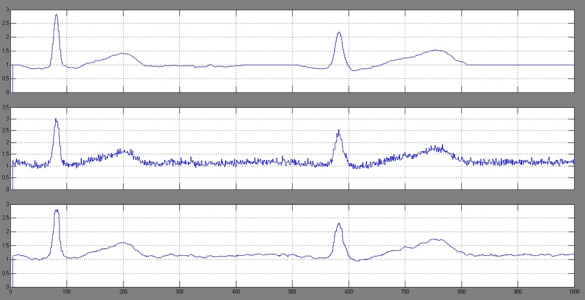Рисунок 3 – Сигнал с наложением райсовского шума

Рисунок 4 показывает результат наложения релеевского шума на фрагмент кардиограммы.

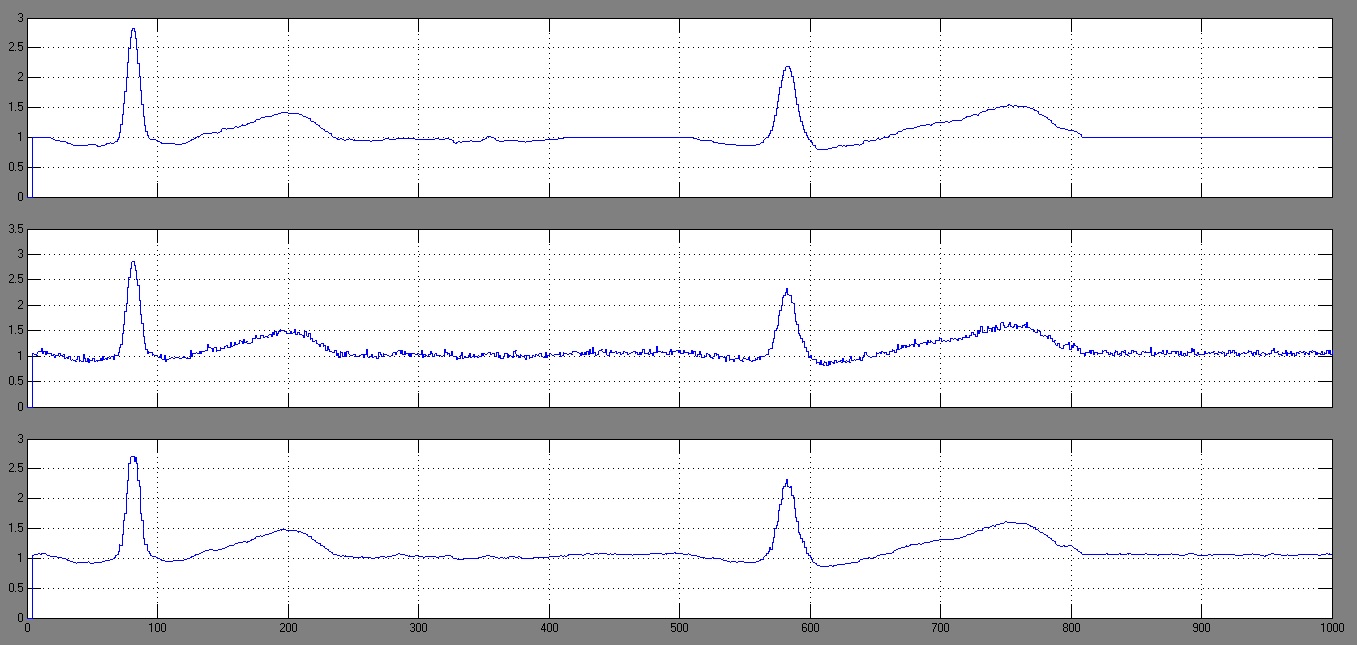Рисунок 4 – Сигнал с наложением релеевского шума

На рисунке 5 представлен график зависимости фильтрации сигналов от соотношения сигнал/шум на входе фильтра (q – мощность сигнала, вх2 – мощность шума). Цифрой 1 обозначен график соотношения сигнала с гауссовским шумом, 2 – с райссовским шумом, 3 – с релеевским шумом.

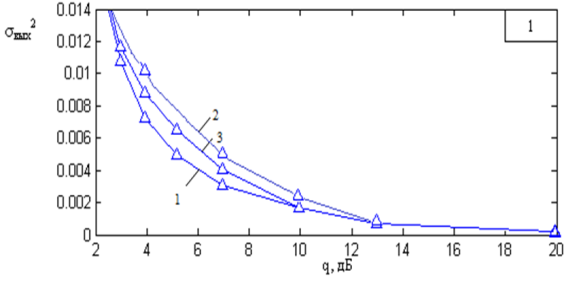Рисунок 5 – соотношения сигнал на шум

Отчетливо видно что при гауссовском шуме ФНЧ хорошо подавляет и восстанавливает исходный сигнал, Средний квадрат ошибки фильтрации видно при соотношении сигнал/шум не превышающем 10-12 дБ. При постоянном соотношении сигнал/шум снижение СКО фильтрации достигает 25%.

ЛИТЕРАТУРА

1. Титов Д.А Алгоритмы цифровой фильтрации сигналов, построенные на базе теории нечетких множеств. Омск-2007.
2. Бычков, Е.Д. Цифровой фильтр на основе теории нечетких множеств с адаптивно изменяющейся функцией принадлежности/ Ю.М. Вешкурцев, Е.Д. Бычков, Д.А. Титов// Изв. вузов России. Радиоэлектроника. - 2007.