–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –≤–Є—А—Г—Б–Њ–≤ –≤ –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є —Б–µ—В–Є
–†—Г–±—А–Є–Ї–∞: –§–Є–Ј–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ12 2017» (–і–µ–Ї–∞–±—А—М, 2017)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 6487
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –≤–Є—А—Г—Б–Њ–≤ –≤ –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є —Б–µ—В–Є
–Ъ–Њ—А–Њ—В–Ї–Њ–≤–∞ –Ф–∞—А—М—П –Р–ї–µ–Ї—Б–µ–µ–≤–љ–∞,
–£–ї—М—П–љ–Њ–≤—Б–Ї–Є–є –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ—Л–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В
—Б—В—Г–і–µ–љ—В–Ї–∞
–Э–∞—Г—З–љ—Л–є —А—Г–Ї–Њ–≤–Њ–і–Є—В–µ–ї—М:
–Р–љ–і—А–µ–µ–≤ –Р–ї–µ–Ї—Б–∞–љ–і—А –°–µ—А–≥–µ–µ–≤–Є—З,
–њ—А–Њ—Д–µ—Б—Б–Њ—А
–Ч–∞—Й–Є—В–∞ –Ї–Њ–Љ–њ—М—О—В–µ—А–Њ–≤ –Є —Б–µ—В–µ–є –Њ—В –≤–Є—А—Г—Б–Њ–≤ —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Њ–є –Є–Ј –≤–∞–ґ–љ—Л—Е –Ј–∞–і–∞—З –љ–∞ —Б–µ–≥–Њ–і–љ—П –≤ IT-–Њ–±–ї–∞—Б—В–Є. –І–Є—Б–ї–Њ –≤—А–µ–і–Њ–љ–Њ—Б–љ–Њ–≥–Њ –њ—А–Њ–≥—А–∞–Љ–Љ–љ–Њ–≥–Њ –Њ–±–µ—Б–њ–µ—З–µ–љ–Є—П –њ–Њ—Б—В–Њ—П–љ–љ–Њ —А–∞—Б—В–µ—В, –∞ —Б–Њ–Ј–і–∞–љ–Є–µ —Б–Њ–≤—А–µ–Љ–µ–љ–љ—Л—Е –Љ–µ—В–Њ–і–Њ–≤ –Ј–∞—Й–Є—В—Л –Њ—В –љ–Њ–≤–Њ–≥–Њ –≤–Є—А—Г—Б–∞ –Ј–∞–љ–Є–Љ–∞–µ—В –і–Њ—Б—В–∞—В–Њ—З–љ–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤—А–µ–Љ–µ–љ–Є. –≠—В–Њ –њ–Њ—А–Њ–ґ–і–∞–µ—В –≥–ї–Њ–±–∞–ї—М–љ—Л–µ —Б–µ—В–µ–≤—Л–µ —Н–њ–Є–і–µ–Љ–Є–Є. –Я–Њ—Н—В–Њ–Љ—Г —Б–Њ–Ј–і–∞–љ–Є–µ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ –Ј–∞—Й–Є—Й–µ–љ–љ—Л—Е —Б–Є—Б—В–µ–Љ –Њ—В –њ—А–Њ–љ–Є–Ї–љ–Њ–≤–µ–љ–Є—П –≤—А–µ–і–Њ–љ–Њ—Б–љ–Њ–≥–Њ –Ї–Њ–і–∞ —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Є–Љ –Є–Ј –∞–Ї—В—Г–∞–ї—М–љ—Л—Е –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–є –≤ –љ–∞—Г—З–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П—Е –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Њ–љ–љ–Њ–є –±–µ–Ј–Њ–њ–∞—Б–љ–Њ—Б—В–Є.
–Ф–ї—П —А–∞–Ј—А–∞–±–Њ—В–Ї–Є —В–∞–Ї–Є—Е —Б–Є—Б—В–µ–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –≤ –Њ–±–ї–∞—Б—В–Є –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є –±–µ–Ј–Њ–њ–∞—Б–љ–Њ—Б—В–Є, –Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞ –і–∞–љ–љ—Л–є –Љ–Њ–Љ–µ–љ—В. –≠—В–Њ –њ–Њ–Ј–≤–Њ–ї–Є—В –≤—Л—П–≤–Є—В—М —А–∞–Ј–ї–Є—З–љ—Л–µ —Б–≤–Њ–є—Б—В–≤–∞ –Є —Д–∞–Ї—В–Њ—А—Л, –≤–ї–Є—П—О—Й–Є–µ –љ–∞ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є–µ –≤–Є—А—Г—Б–∞. –Ю–і–љ–Є–Љ –Є–Ј –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є —П–≤–ї—П–µ—В—Б—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ.
–Т –і–∞–љ–љ–Њ–є —Б—В–∞—В—М–µ –Є–Ј—Г—З–∞–µ—В—Б—П, –љ–∞–Є–±–Њ–ї–µ–µ –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–∞—П –Ї —А–µ–∞–ї—М–љ—Л–Љ —Г—Б–ї–Њ–≤–Є—П–Љ, –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П –Љ–Њ–і–µ–ї—М —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –≤–Є—А—Г—Б–Њ–≤ PSIDR.
–Ъ–ї—О—З–µ–≤—Л–µ —Б–ї–Њ–≤–∞: –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ, PSIDR, –Ј–∞–њ–∞–Ј–і—Л–≤–∞–љ–Є–µ.
–Ю—Б–љ–Њ–≤–љ–Њ–є —Н—В–∞–њ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П —Н–њ–Є–і–µ–Љ–Є–Є –≤—А–µ–і–Њ–љ–Њ—Б–љ—Л—Е –њ—А–Њ–≥—А–∞–Љ–Љ вАФ –≤—Л–±–Њ—А —Н–њ–Є–і–µ–Љ–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є –Љ–Њ–і–µ–ї–Є, –∞–і–µ–Ї–≤–∞—В–љ–Њ –Њ–њ–Є—Б—Л–≤–∞—О—Й–µ–є —Н—В–Њ—В –њ—А–Њ—Ж–µ—Б—Б. –С–Њ–ї—М—И–Є–љ—Б—В–≤–Њ –Є—Б—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–µ–є –≤ –Њ–±–ї–∞—Б—В–Є –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е –≤–Є—А—Г—Б–Њ–≤ –њ—А–Њ–≤–Њ–і—П—В –∞–љ–∞–ї–Њ–≥–Є—О –Љ–µ–ґ–і—Г –≤—А–µ–і–Њ–љ–Њ—Б–љ—Л–Љ –њ—А–Њ–≥—А–∞–Љ–Љ–љ—Л–Љ –Њ–±–µ—Б–њ–µ—З–µ–љ–Є–µ–Љ –Є –њ—А–Є—А–Њ–і–љ—Л–Љ–Є –≤–Є—А—Г—Б–∞–Љ–Є, —Б–µ—В–µ–≤–Њ–є —Н–њ–Є–і–µ–Љ–Є–µ–є –Є –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є —Н–њ–Є–і–µ–Љ–Є–µ–є.
–° –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –Њ—А–≥–∞–љ–Є—З–µ—Б–Ї–Є–µ –Є –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л–µ –≤–Є—А—Г—Б—Л –Є–Љ–µ—О—В —Б—Е–Њ–ґ–Є–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –Є —Б–≤–Њ–є—Б—В–≤–∞, –Є—Е —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є–µ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П —Б—Е–Њ–і–љ—Л–Љ–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–Љ–Є —Г—А–∞–≤–љ–µ–љ–Є—П–Љ–Є. –Ш—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є—Е –і–∞–љ–љ—Л—Е —В–∞–Ї–ґ–µ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –∞–і–µ–Ї–≤–∞—В–љ–Њ—Б—В—М –њ—А–Є–Љ–µ–љ–µ–љ–Є—П –Љ–Њ–і–µ–ї–Є —Н–њ–Є–і–µ–Љ–Є–Є –Є–љ—Д–µ–Ї—Ж–Є–Њ–љ–љ—Л—Е –Ј–∞–±–Њ–ї–µ–≤–∞–љ–Є–є –і–ї—П –Њ–њ–Є—Б–∞–љ–Є—П –њ—А–Њ—Ж–µ—Б—Б–∞ —А–∞–Ј–≤–Є—В–Є—П –≤–Є—А—Г—Б–љ–Њ–є –∞—В–∞–Ї–Є. –Я–Њ—Н—В–Њ–Љ—Г –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ —В–µ–Њ—А–Є–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ –њ–Њ–ї—Г—З–Є–ї–Њ –±–Њ–ї—М—И–Њ–µ —А–∞–Ј–≤–Є—В–Є–µ –≤ –љ–∞—Г—З–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П—Е –њ–Њ –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є –±–µ–Ј–Њ–њ–∞—Б–љ–Њ—Б—В–Є.
–Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –Є–Ј–≤–µ—Б—В–љ–Њ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–µ–є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е –Љ–Њ–і–µ–ї–µ–є —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е –≤–Є—А—Г—Б–Њ–≤, –Ї–Њ—В–Њ—А—Л–µ –Њ—В–ї–Є—З–∞—О—В—Б—П –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є –Њ–±–ї–∞—Б—В—М—О –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –Є —Г—Б–ї–Њ–≤–Є—П–Љ–Є –њ—А–Є–Љ–µ–љ–µ–љ–Є—П –≤ —А–µ–∞–ї—М–љ—Л—Е —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ–∞—Е.
–°—А–µ–і–Є –љ–Є—Е –Љ–Њ–ґ–љ–Њ –≤—Л–і–µ–ї–Є—В—М —Б–ї–µ–і—Г—О—Й–Є–µ –Љ–Њ–і–µ–ї–Є: SI, SIR, AAWP, PSIDR.
–Ь–Њ–і–µ–ї—М SI —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В—Б—П –љ–∞–ї–Є—З–Є–µ–Љ –і–≤—Г—Е —В–Є–њ–Њ–≤ –Њ–±—К–µ–Ї—В–Њ–≤ —Г–њ—А–∞–≤–ї–µ–љ–Є—П: –Ј–∞—А–∞–ґ–µ–љ–љ—Л–µ (I) –Є –љ–µ –Ј–∞—А–∞–ґ–µ–љ–љ—Л–µ (S). –•–∞—А–∞–Ї—В–µ—А–љ–Њ–є –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В—М—О SI –Љ–Њ–і–µ–ї–Є —П–≤–ї—П–µ—В—Б—П –њ—А–µ–љ–µ–±—А–µ–ґ–µ–љ–Є–µ –∞–љ—В–Є–≤–Є—А—Г—Б–љ—Л–Љ –Я–Ю, —З—В–Њ –њ—А–Є–≤–Њ–і–Є—В –Ї –љ–µ–Њ–±—А–∞—В–Є–Љ–Њ—Б—В–Є —Н–њ–Є–і–µ–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –≤ –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е —Б–Є—Б—В–µ–Љ–∞—Е.
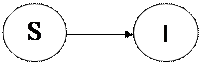
–†–Є—Б 1. –У—А–∞—Д —Б–Њ—Б—В–Њ—П–љ–Є–є –Љ–Њ–і–µ–ї–Є SI.
–§–Њ—А–Љ–∞–ї—М–љ–Њ, —Н—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Г—Б–њ–µ—И–љ–Њ–≥–Њ —А–∞–Ј–Љ–љ–Њ–ґ–µ–љ–Є—П –≤–Є—А—Г—Б–∞ —Б–Њ—Б—В–∞–≤–Є—В
![]()
–Я—А–Є—А–∞—Й–µ–љ–Є–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤–Є—А—Г—Б–∞ –љ–∞ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –Љ–∞–ї–Њ–Љ –Є–љ—В–µ—А–≤–∞–ї–µ
![]() , –∞ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ, –Ї–Њ—В–Њ—А–Њ–µ –Њ–њ–Є—Б—Л–≤–∞–µ—В –і–Є–љ–∞–Љ–Є–Ї—Г —Н–њ–Є–і–µ–Љ–Є–є, –±—Г–і–µ—В –≤—Л–≥–ї—П–і–µ—В—М —В–∞–Ї:
, –∞ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ, –Ї–Њ—В–Њ—А–Њ–µ –Њ–њ–Є—Б—Л–≤–∞–µ—В –і–Є–љ–∞–Љ–Є–Ї—Г —Н–њ–Є–і–µ–Љ–Є–є, –±—Г–і–µ—В –≤—Л–≥–ї—П–і–µ—В—М —В–∞–Ї:
![]()
–†–µ—И–µ–љ–Є–µ —Н—В–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –Ј–∞–њ–Є—Б—Л–≤–∞–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
–Ъ–Њ–љ—Б—В–∞–љ—В–∞ ![]() —Г—З–Є—В—Л–≤–∞–µ—В –љ–∞—З–∞–ї—М–љ–Њ–µ —Г—Б–ї–Њ–≤–Є–µ
—Г—З–Є—В—Л–≤–∞–µ—В –љ–∞—З–∞–ї—М–љ–Њ–µ —Г—Б–ї–Њ–≤–Є–µ ![]() .
.
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є I(t) –љ–∞ –љ–∞—З–∞–ї—М–љ–Њ–Љ —Н—В–∞–њ–µ –≤–µ–і–µ—В —Б–µ–±—П, –Ї–∞–Ї —Н–Ї—Б–њ–Њ–љ–µ–љ—В–∞, –љ–Њ –Ј–∞—В–µ–Љ –Ј–∞–Љ–µ–і–ї—П–µ—В —Б–≤–Њ–є —А–Њ—Б—В –Є —Б—В—А–µ–Љ–Є—В—Б—П –Ї –∞—Б–Є–Љ–њ—В–Њ—В–µ N.
–Т —Б–≤—П–Ј–Є —Б –Њ—В—Б—Г—В—Б—В–≤–Є–µ–Љ –∞–љ—В–Є–≤–Є—А—Г—Б–∞, –Ї–Њ—В–Њ—А—Л–є –≤–ї–Є—П–µ—В –љ–∞ –њ—А–Њ—Ж–µ—Б—Б —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е –≤–Є—А—Г—Б–Њ–≤, —Н–њ–Є–і–µ–Љ–Є—П –љ–µ –Љ–Њ–ґ–µ—В —Г–≥–∞—Б–љ—Г—В—М. –Ъ—А–Є–≤—Л–µ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е —Г–Ј–ї–Њ–≤ –Њ—В –≤—А–µ–Љ–µ–љ–Є —Д—Г–љ–Ї—Ж–Є–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –≤ —Г—Б–ї–Њ–≤–Є—П—Е —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П —Н–њ–Є–і–µ–Љ–Є–Є –њ–Њ –Љ–Њ–і–µ–ї–Є SI –њ—А–Є —А–∞–Ј–љ—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞—Е –Ј–∞—А–∞–ґ–µ–љ–Є—П b –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л –љ–∞ —А–Є—Б. 2.
–Р–љ–∞–ї–Є–Ј –≥—А–∞—Д–Є–Ї–Њ–≤ –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Ј–∞—А–∞–ґ–µ–љ–Є—П b –њ—А—П–Љ–Њ–њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ –≤–ї–Є—П–µ—В –љ–∞ —Б–Ї–Њ—А–Њ—Б—В—М —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –≤–Є—А—Г—Б–∞.
–†–Є—Б 2. –Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е —Б—Г–±—К–µ–Ї—В–Њ–≤ –≤ –Љ–Њ–і–µ–ї–Є SI.
–Ь–Њ–і–µ–ї—М PSIDR (Progressive SusceptibleвАФInfectedвАФDetectedвАФRemoved model) —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В—Б—П –љ–∞–ї–Є—З–Є–µ–Љ —З–µ—В—Л—А–µ—Е —Б–Њ—Б—В–Њ—П–љ–Є–є: –Ј–∞—А–∞–ґ–µ–љ–љ—Л–µ (I), –љ–µ –Ј–∞—А–∞–ґ–µ–љ–љ—Л–µ (S), –љ–∞–є–і–µ–љ–љ—Л–µ –Ј–∞—А–∞–ґ–µ–љ–љ—Л–µ –Њ–±—К–µ–Ї—В—Л (D), –≤—Л–ї–µ—З–µ–љ–љ—Л–µ –Њ–±—К–µ–Ї—В—Л, –Њ–±–ї–∞–і–∞—О—Й–Є–µ –Є–Љ–Љ—Г–љ–Є—В–µ—В–Њ–Љ ¬Ѓ. –Я–Њ–≤–µ–і–µ–љ–Є–µ —Б–Є—Б—В–µ–Љ—Л, –Њ–њ–Є—Б–∞–љ–љ–Њ–µ —Б –њ–Њ–Љ–Њ—Й—М—О –Љ–Њ–і–µ–ї–Є PSIDR, –і–µ–ї–Є—В—Б—П –љ–∞ –і–≤–∞ —Н—В–∞–њ–∞:
–Я–µ—А–Є–Њ–і —Б–≤–Њ–±–Њ–і–љ–Њ–≥–Њ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –≤–Є—А—Г—Б–∞ –≤ —Б–µ—В–Є.
–Т–Є—А—Г—Б —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ—П–µ—В—Б—П —Б–Њ–≥–ї–∞—Б–љ–Њ SI –Љ–Њ–і–µ–ї–Є –≤ —В–µ—З–µ–љ–Є–µ –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є —Б–Њ —Б–Ї–Њ—А–Њ—Б—В—М—О ќ≤.
–Я–µ—А–Є–Њ–і –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –≤—А–µ–і–Њ–љ–Њ—Б–љ–Њ–≥–Њ –Я–Ю.
–Т —Н—В–Њ–є —Д–∞–Ј–µ —Б–Ї–Њ—А–Њ—Б—В—М —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –Њ—Б—В–∞–µ—В—Б—П –њ—А–µ–ґ–љ–µ–є, –≤–Њ—Б–њ—А–Є–Є–Љ—З–Є–≤—Л–µ —Б—Г–±—К–µ–Ї—В—Л –≤–∞–Ї—Ж–Є–љ–Є—А—Г—О—В—Б—П —Б–Њ —Б–Ї–Њ—А–Њ—Б—В—М—О ¬µ, –∞ –Є–љ—Д–Є—Ж–Є—А–Њ–≤–∞–љ–љ—Л–µ –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞—О—В—Б—П —Б–Њ —Б–Ї–Њ—А–Њ—Б—В—М—О ¬µ –Є ¬Ђ–ї–µ—З–∞—В—Б—П¬ї —Б–Њ —Б–Ї–Њ—А–Њ—Б—В—М—О бЇЯ.
–†–Є—Б 3. –У—А–∞—Д —Б–Њ—Б—В–Њ—П–љ–Є–є –≤—В–Њ—А–Њ–≥–Њ —Н—В–∞–њ–∞ PSIDR.
–Ь–Њ–і–µ–ї—М —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –≤–Є—А—Г—Б–Њ–≤ –≤ –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є —Б–µ—В–Є PSIDR, –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Њ—Ж–µ–љ–Є—В—М –і–Є–љ–∞–Љ–Є–Ї—Г –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —Г—П–Ј–≤–Є–Љ—Л—Е, –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е, –љ–∞–є–і–µ–љ–љ—Л—Е –Є –Є–Љ–µ—О—Й–Є—Е –Є–Љ–Љ—Г–љ–Є—В–µ—В —Б—Г–±—К–µ–Ї—В–Њ–≤, –Є –Љ–Њ–ґ–µ—В –±—Л—В—М –Ј–∞–њ–Є—Б–∞–љ–∞ —Б –њ–Њ–Љ–Њ—Й—М—О —Б–Є—Б—В–µ–Љ—Л –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є —Б –Ј–∞–њ–∞–Ј–і—Л–≤–∞–љ–Є–µ–Љ:
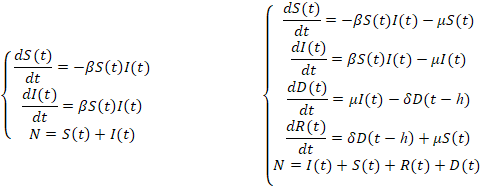
–≥–і–µ b вАФ —З–∞—Б—В–Њ—В–∞ –Ј–∞—А–∞–ґ–µ–љ–Є—П; d вАФ —З–∞—Б—В–Њ—В–∞ –ї–µ—З–µ–љ–Є—П; m вАФ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –≤—Л–ї–µ—З–Є–≤–∞–љ–Є—П, S(t) вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —Г—П–Ј–≤–Є–Љ—Л—Е –Њ–±—К–µ–Ї—В–Њ–≤; I(t) вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е –Њ–±—К–µ–Ї—В–Њ–≤; R(t) вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤—Л–ї–µ—З–µ–љ–љ—Л—Е (—Б –Є–Љ–Љ—Г–љ–Є—В–µ—В–Њ–Љ) –Њ–±—К–µ–Ї—В–Њ–≤ (–љ–∞ –њ–µ—А–≤–Њ–є —Б—В–∞–і–Є–Є = 0); D(t) вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ—Л—Е –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е –Њ–±—К–µ–Ї—В–Њ–≤ (–љ–∞ –њ–µ—А–≤–Њ–є —Б—В–∞–і–Є–Є = 0).
–Ъ—А–Є–≤–∞—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ—Л—Е —Г–Ј–ї–Њ–≤ –Њ—В –≤—А–µ–Љ–µ–љ–Є —Д—Г–љ–Ї—Ж–Є–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –њ–Њ –Љ–Њ–і–µ–ї–Є PSIDR –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–∞ –љ–∞ —А–Є—Б. 4.
–†–Є—Б 4. –У—А–∞—Д–Є–Ї –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ—Л—Е –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е –Ї–Њ–Љ–њ—М—О—В–µ—А–Њ–≤ –Њ—В –≤—А–µ–Љ–µ–љ–Є –≤ –Љ–Њ–і–µ–ї–Є PSIDR.
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ—Л—Е –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е –Њ–±—К–µ–Ї—В–Њ–≤ ![]() —Б—В—А–µ–Љ–Є—В—Б—П –Ї –љ—Г–ї—О. –†–µ—И–µ–љ–Є—П –Љ–Њ–≥—Г—В –Є–Љ–µ—В—М –Ї–∞–Ї —Е–∞—А–∞–Ї—В–µ—А –Ј–∞—В—Г—Е–∞—О—Й–Є—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є (—А–Є—Б. 5), —В–∞–Ї –Є –∞–њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Є–є —Е–∞—А–∞–Ї—В–µ—А (—А–Є—Б. 6). –Т—Б—С –Ј–∞–≤–Є—Б–Є—В –Њ—В –њ–∞—А–∞–Љ–µ—В—А–∞ –Ј–∞–њ–∞–Ј–і—Л–≤–∞–љ–Є—П.
—Б—В—А–µ–Љ–Є—В—Б—П –Ї –љ—Г–ї—О. –†–µ—И–µ–љ–Є—П –Љ–Њ–≥—Г—В –Є–Љ–µ—В—М –Ї–∞–Ї —Е–∞—А–∞–Ї—В–µ—А –Ј–∞—В—Г—Е–∞—О—Й–Є—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є (—А–Є—Б. 5), —В–∞–Ї –Є –∞–њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Є–є —Е–∞—А–∞–Ї—В–µ—А (—А–Є—Б. 6). –Т—Б—С –Ј–∞–≤–Є—Б–Є—В –Њ—В –њ–∞—А–∞–Љ–µ—В—А–∞ –Ј–∞–њ–∞–Ј–і—Л–≤–∞–љ–Є—П.
–†–Є—Б 5. –У—А–∞—Д–Є–Ї –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ—Л—Е –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е –Ї–Њ–Љ–њ—М—О—В–µ—А–Њ–≤ –Њ—В –≤—А–µ–Љ–µ–љ–Є –≤ –Љ–Њ–і–µ–ї–Є PSIDR —Б h = 1.
–†–Є—Б 6. –У—А–∞—Д–Є–Ї –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ–±–љ–∞—А—Г–ґ–µ–љ–љ—Л—Е –Ј–∞—А–∞–ґ–µ–љ–љ—Л—Е –Ї–Њ–Љ–њ—М—О—В–µ—А–Њ–≤ –Њ—В –≤—А–µ–Љ–µ–љ–Є –≤ –Љ–Њ–і–µ–ї–Є PSIDR —Б h = 0.1.
–†–Є—Б 7. –У—А–∞—Д–Є–Ї –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Є–љ—Д–Є—Ж–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б—Г–±—К–µ–Ї—В–Њ–≤
–Њ—В –≤—А–µ–Љ–µ–љ–Є –≤ –Љ–Њ–і–µ–ї–Є PSIDR.
–Я—А–Њ–≤–µ–і–µ–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј –Љ–Њ–і–µ–ї–Є PSIDR –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –Њ–љ–∞ —П–≤–ї—П–µ—В—Б—П –љ–∞–Є–±–Њ–ї–µ–µ –њ–Њ–і—А–Њ–±–љ–Њ–є, —В–∞–Ї –Ї–∞–Ї —А–∞–Ј–±–Є–µ–љ–Є–µ –Љ–Њ–і–µ–ї–Є —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е —Г–≥—А–Њ–Ј –љ–∞ –і–≤–∞ —Н—В–∞–њ–∞ –і–∞–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ –њ—А–Њ—Ж–µ—Б—Б–∞ –Ј–∞—А–∞–ґ–µ–љ–Є—П –Є –ї–µ—З–µ–љ–Є—П, –∞ –≤–≤–µ–і–µ–љ–Є–µ –Ј–∞–њ–∞–Ј–і—Л–≤–∞–љ–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ–Њ ¬Ђ–љ–µ–Љ–≥–љ–Њ–≤–µ–љ–љ–Њ–є¬ї —А–µ–∞–Ї—Ж–Є–µ–є –∞–љ—В–Є–≤–Є—А—Г—Б–∞ –љ–∞ –Є–љ—Д–Є—Ж–Є—А–Њ–≤–∞–љ–љ—Л–µ —Б—Г–±—К–µ–Ї—В—Л.
–Ы–Є—В–µ—А–∞—В—Г—А–∞
- –Ъ–Њ—В–µ–љ–Ї–Њ –Ш.–Т. –Р–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Є–µ –Љ–Њ–і–µ–ї–Є —А–∞—Б–њ—А–Њ—Б—В—А–∞- –љ–µ–љ–Є—П —Б–µ—В–µ–≤—Л—Е —З–µ—А–≤–µ–є / –Ш.–Т. –Ъ–Њ—В–µ–љ–Ї–Њ, –Т.–Т. –Т–Њ—А–Њ–љ—Ж–Њ–≤ // –Ґ—А—Г–і—Л –°–Я–Ш–Ш–†–Р–Э. вАФ –°–Я–±.: –Э–∞—Г–Ї–∞, 2007. вАФ –Т—Л–њ. 4.
- Williamson M. Epidemiological model of virus spread and cleanup [–≠–ї–µ–Ї—В—А–Њ–љ–љ—Л–є —А–µ—Б—Г—А—Б] / M. Williamson, J. Leveille // HP Laboratories Bristol (February 27th, 2003).
- –°—В–Њ–ї–Є–љ–≥—Б, –Т. –Ю—Б–љ–Њ–≤—Л –Ј–∞—Й–Є—В—Л —Б–µ—В–µ–є. –Я—А–Є–ї–Њ–ґ–µ–љ–Є—П –Є —Б—В–∞–љ–і–∞—А- —В—Л / –Т. –°—В–Њ–ї–ї–Є–љ–≥—Б. вАФ –Ь. : –Т–Є–ї—М—П–Љ—Б, 2002. вАФ 432 —Б. вАФ ISBN
5-8459-0298-3. - Daley, D.J. and Gani, J. Epidemic Modeling: An Introduction. Cambridge University Press, 1999.









