Истины математики, физики, технических дисциплин

Ключевые слова: плазма; плотности; радиальная расходимость; токамак.

1. Математика. Геометрия.

Физические тела имеют геометрическую форму в виде разнообразных фигур. Геометрические параметры – длина, ширина, длина периметра; высота, радиус (у фигур вращения); площадь поверхности; объём. Геометрические фигуры характеризуются соотношениями длины периметра к площади (плоские фигуры) и площади поверхности к объёму (объёмные фигуры). Эти характеристики имеют практическое значение, например длина забора на единицу площади участка и площадь поверхности сосудов данной ёмкости. Существуют стандартные решения практических задач по оптимизации отношения площади поверхности к объёму тела. [1, c. 178-180].

Рассмотрим известные плоские фигуры. Круг – односвязная область плоскости; геометрическая фигура без отверстий. [2, c. 141]

Плоское круглое кольцо – не односвязная, двусвязная область плоскости; геометрическая фигура с отверстием в центре фигуры [2, c.141; 4, с.404], рисунок 1:

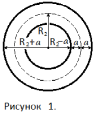
R2 – радиус средней окружности кольца шириной 2a. Средняя окружность разделяет кольцо на две части, каждая шириной a: внешнюю, большую часть кольца и внутреннюю, меньшую часть кольца.

(R2 + a) – внешний, или большой радиус кольца шириной 2a

(R2 – a) – внутренний, или малый радиус кольца шириной 2a

Приведенные формулы показывают: периметр всего плоского кольца равен двум длинам средней окружности кольца (5); при равной площади кольцо имеет большую длину периметра, чем круг; при увеличении ширины кольца увеличивается его площадь на единицу длины периметра; при уменьшении ширины кольца уменьшается площадь на единицу длины периметра (6). Радиальная расходимость – геометрическое свойство плоского кольца: внешняя часть кольца за средней окружностью имеет большую площадь и периметр, чем внутренняя часть кольца (7, 8, 9, 10).

Рассмотрим известные объёмные фигуры. Шар – односвязная объёмная область пространства; объём без внутренних полостей, сквозных отверстий и промежутков [3, c. 48, с. 102].

Примером односвязной объёмной области пространства также является цилиндр.

Тор, или “бублик” – геометрическая фигура вращения радиусом R вокруг центра тора о (на оси b – d) центра k образующей окружности радиуса r; объём с внутренним промежутком [3, c. 48, с. 102], рисунки 2, 3, 4. Центр тяжести тора расположен в геометрическом центре тора - точке о, вне объёма тора.

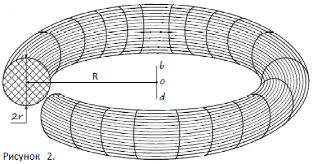
Представим сечение тора средним цилиндром радиуса R, ось которого совпадает с осью тора b – d. Результат сечения – внешняя, большая часть тора (рисунок 3) и внутренняя, меньшая часть тора (рисунок 4).

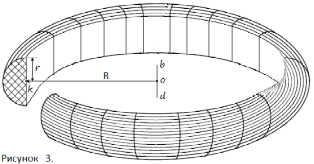
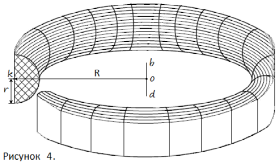
Объёмы и площади криволинейных поверхностей частей тора определяются по теоремам Гульдина [ 1, c. 329 – 332].

Формулы показывают: шар имеет меньшую площадь поверхности, чем тор при их равном объёме (11, 12, 15, 16). Радиальная расходимость – геометрическое свойство тора: внешняя часть тора за средним цилиндром имеет большую площадь поверхности и объём, чем внутренняя часть тора (19, 20, 21, 22).

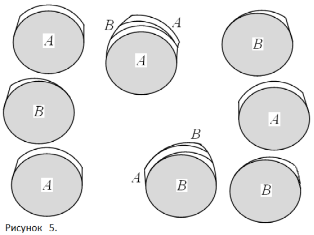
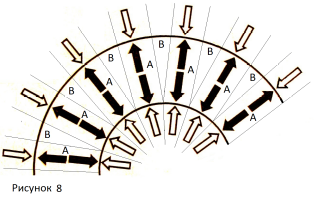
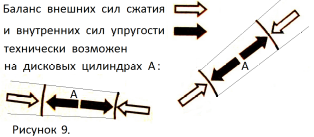
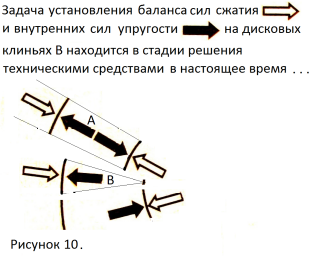
Объём тора можно представить состоящим из последовательно чередующихся цилиндрических дисков, похожих на монеты (условно обозначены А на рисунках 5, 8, 9, 10) и дисковых клиньев, похожих на дольки мандарина (условно обозначены В на рисунках 5, 8, 10). Фрагменты тора – АВА и ВАВ. При уменьшении r уменьшаются дисковые клинья В, но не исчезают.

2. Физика.

Рассмотрим плотности. Объёмная плотность веществ известна из школьных курсов природоведения, физики, химии. Плотность показывает концентрацию – распределение массы вещества, или энергии, или мощности, или действующих сил, или каких – либо других скалярных или векторных величин по объёму, или площади поверхности, или линии. Мощность – временная плотность энергии.

Плотность тока - это сила электрического тока, протекающего через единицу поперечного сечения проводника, широко применяется на практике. В разных разделах электротехники, электроники, радиотехники, приборостроения существуют рабочие таблицы и адаптированные формулы для инженерных расчётов, используемые при конструировании и эксплуатации конкретных приборов, устройств, систем, их фрагментов.

Плотности распределения скалярных или векторных величин вносят ясность, наглядность в понимание самых разных процессов, позволяют эффективно решать инженерные задачи. Объёмная плотность мощности существует в определениях [5, c.70]. На практике двигатели внутреннего сгорания (ДВС) характеризуются мощностью и рабочим объёмом цилиндров.

В экспериментах (проведенных в 1988 и 1989 годах) на импульсном технологическом лазере [6, 7] в линиях реза конструкционных материалов получалась объёмная плотность мощности до 12 киловатт на кубический миллиметр, что соответствует 12 мегаватт на кубический сантиметр в стабильном, надёжно управляемом процессе (рис 6). При этом импульсный твердотельный лазер со средней мощностью луча 100 – 250 Ватт разрезал пластины из дюралевых и медных сплавов, которые не разрезал газовый лазер с мощностью луча 2500 Ватт в непрерывном режиме. Этот факт говорит о нелинейности локальной теплопроводности, других свойств материалов при их обработке импульсными воздействиями.

На рисунке 6 одно деление линейных шкал равно одному миллиметру, цифрами обозначены:

1 - пластина из дюралевого сплава;

2 - линия реза импульсным лазером [6, 7] с объёмной плотностью мощности до 12 киловатт на кубический миллиметр;

3 - фрагменты изделий из листовой стали;

4 - линия реза серийным лазером ЛТН-103 в непрерывном режиме с объёмной плотностью мощности 500 Ватт на кубический миллиметр;

5 - листки бумаги толщиной 0,05 миллиметра.

В настоящее время техника и технологии позволяют повышать уровень объёмной плотности мощности в экспериментах при стабильном, надёжно управляемом процессе.

Для сравнения: объёмная плотность мощности ДВС 40 – 60 Ватт на кубический сантиметр (по рабочему объёму цилиндров); электродвигателей общего применения 0,5 – 2 Ватта на кубический сантиметр [5, c. 557-559].

Пример наглядности: объём спички бытовой ГОСТ 1820 – 2001 равен 160 кубических миллиметров, спичечного коробка – 21 кубический сантиметр. Лазерная техника и технологии позволяют концентрировать мощность 1 мегаватт в половину объёма одной спички, мощность 100 киловатт (ДВС) в двадцатую часть объёма одной спички. При этом объём силовых трансформаторов в 1 мегаватт составляет от 8 до 12 кубических метров [5, c. 404].

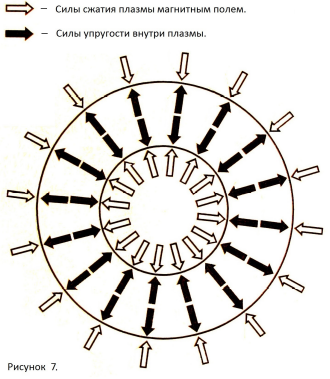
Энергоёмкой экспериментальной установкой является токамак. [8, 9, 10, c. 502-507]. Токама́к – тороидальная вакуумная установка для магнитного удержания плазмы с целью достижения условий, необходимых для протекания управляемого термоядерного синтеза. Плазма в токамаке сжимается и удерживается специально создаваемым комбинированным магнитным полем – тороидальным внешним и полоидальным полем тока, протекающего по плазменному шнуру на средней окружности тора. Сечение тора в плоскости, проходящей через центр тора перпендикулярно его оси – это кольцо. На рисунках 7, 8, 9, 10 контурными стрелками обозначены силы сжатия плазмы магнитным полем. Чёрными стрелками обозначены силы упругости внутри сжимаемой плазмы. Радиальная расходимость тора – причина разной "густоты" стрелок на внутренней и внешней окружностях кольца. Рассмотрим распределение плотностей по объёму тора. Жидкости, газы, пары веществ, плазма (как ионизированный газ) стремятся заполнить занимаемый объём с равномерной объёмной плотностью массы. Следовательно, перед сжатием во внешней части тора имеется большая масса плазмы, чем во внутренней части тора. Магнитная система создаёт неравномерное магнитное поле из-за геометрической радиальной расходимости тора. На внутреннюю часть плазмы в торе действуют с большей плотностью силы магнитных полей при меньшей массе и объёме плазмы (рис. 7, 8), чем на внешнюю часть плазмы в торе при большей массе и объёме плазмы.

Следовательно, единица массы и объёма внутренней части тороидальной плазмы в процессе сжатия получает большую энергию от сжимающего магнитного поля, становится более энергоёмкой, чем единица массы и объёма внешней части тороидальной плазмы. Это является фактором нестабильности сжимаемой плазмы в тороидальной камере. Возникают колебания в плазменном шнуре и отклонения его от окружности. Представим процесс сжатия как встречное движение фронтов, набирающих кинетическую энергию в период сжатия: внешний, больший по объёму и массе, менее энергоёмкий, энергетически “рыхлый” фронт, встречается в узком шнуре с более энергоёмким внутренним фронтом, который разрывает “рыхлый” внешний фронт. Дисковые клинья В (рисунки 5, 8, 10) способствуют соскальзыванию со средней окружности какого-либо фрагмента АВА…ВА шнура плазмы. Следовательно, разрушение тороидального плазменного шнура в установках типа “токамак” закономерно.

 3. Технические дисциплины.

Из технических дисциплин в этой статье кратко рассмотрим теорию управления (ТУ) техническими устройствами, системами и теорию автоматического управления (ТАУ). Концепции, принципы и механизмы управления, алгоритмы, математические уравнения, описание физических и технических основ подробно изложены во многих книгах по ТУ и ТАУ. Например, можно обратиться к [11, 12]. Общепринятого определения “управления” не существует в настоящее время. Авторы книг и статей публикуют свои варианты по разным причинам. Возможно представить изложение материалов из книг по ТУ и ТАУ следующим образом: управление – действие субъекта на объект управления для достижения результатов. В технических изделиях, системах между субъектом и объектом управления расположены устройства, механизмы или системы управления. Управляемость – свойство объекта, субъекта, системы управления, их общая способность “приходить” к заданному результату. Существует высокий уровень техники, алгоритмов и программ управления движением летательных аппаратов (ЛА). Управляемость ЛА и других движущихся объектов получается при контролируемом балансе сил: движущих (ДС), управляющих (УС), опорных (ОС), сил сопротивления среды (ССС) в каждый момент времени по всей траектории движения от запуска до остановки рабочего процесса (РП) системы или устройства. РП характеризуется определёнными параметрами, которые связаны дифференциальным уравнением или системой дифференциальных уравнений, которые в свою очередь определяют зоны числовых значений параметров РП: устойчивой зоны, неустойчивой зоны, деструктивно-разрушительной зоны, границы между ними.

Мотор, двигательные устройства и механизмы создают ДС.

ОС возникают в среде необходимой плотности, определяющей прочность опоры проводимого РП. ССС возникают как ответная реакция среды на её изменение движущимся объектом.

УС создаются рулевыми механизмами в движущихся объектах и регулирующими системами в недвижимых процессах (энергетических, химических реакторах). Все системы стабильного эффективного управления самолётами, ракетами, автомобилями и другими движущими объектами основаны на манипулировании устройствами управления вокруг центра воздействия. Центр воздействия и центр масс (центр тяжести) находятся внутри объёма ЛА при хорошей управляемости. Рычаги управления, рулевые устройства, приводные механизмы управления созданы так, что управляющие силы приводятся к центру воздействия. Штатное взаимодействие центра воздействия и центра масс ЛА обеспечивает нормальный полёт ЛА.

При отсутствии заданных результатов в управлении говорят о неуправляемости. История техники и здравый смысл подсказывают, что неуправляемость чего – либо приводит к изменению или замене: объекта или субъекта управления; устройств, механизмов, систем управления; алгоритмов управления. Или поиску новых концепций, технических и физических основ для достижения результатов.

Продолжение следует...

Борис Ревашин, 17 августа 2016 года.

Литература:

1. Фролов Н. А. Дифференциальное и интегральное исчисление. М., 1955, 339с.

2. Кудрявцев Л. Д. Математический анализ. том II М., Высшая школа, 1970, 420 с.

3. Корн Г., Корн Т. Справочник по математике. 6-е изд., Спб., 2003, 832 с.

4. Буров Я. С., Никольский С. М. Высшая математика. 4-е изд. Ростов н/Д: «Феникс», 1998, 512 с.

5. Электротехнический справочник. Т. 1, М., Энергия, 1974, 776 с.

6. Авторское свидетельство SU 1810262, В23К 26/00, опубликовано 23.04.1993г.

7. Патент RU 2368108 С2 Н05В41/28, опубликован 20.09.2009г.

8. Сайт в сети интернет: www.wikipedia.org/wiki/Токамак

9. Сайт НИЦ "Курчатовский институт" в сети интернет: www.nrcki.ru

10. Яворский Б. М., Пинский А. А. Основы физики. т. 2, М, 2003, 552 с.

11. Бесекерский В.А. Теория систем автоматического управления. Спб., 2003, 752 с.

12. Лукас В.А. Теория управления техническими системами. Екатеринбург, 2002, 675 с.