–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ш—Б—В–Є–љ—Л –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є, —Д–Є–Ј–Є–Ї–Є, —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –і–Є—Б—Ж–Є–њ–ї–Є–љ.
–†—Г–±—А–Є–Ї–∞: –Ґ–µ—Е–љ–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ12 2017» (–і–µ–Ї–∞–±—А—М, 2017)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 2615
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ш—Б—В–Є–љ—Л –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є, —Д–Є–Ј–Є–Ї–Є, —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –і–Є—Б—Ж–Є–њ–ї–Є–љ.
–†–µ–≤–∞—И–Є–љ –С–Њ—А–Є—Б –У–µ–љ–љ–∞–і—М–µ–≤–Є—З
–°—В–∞—В—М—П –≤—В–Њ—А–∞—П, –њ—А–Њ–і–Њ–ї–ґ–µ–љ–Є–µ —Б—В–∞—В—М–Є –Њ—В 17 –∞–≤–≥—Г—Б—В–∞ 2016 –≥–Њ–і–∞, –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ–љ–Њ–є –≤ вДЦ 8 ¬Ђ–Х–≤—А–∞–Ј–Є–є—Б–Ї–Њ–≥–Њ –љ–∞—Г—З–љ–Њ–≥–Њ –ґ—Г—А–љ–∞–ї–∞¬ї –Ј–∞ 2016 –≥–Њ–і. –Я—А–Њ–і–Њ–ї–ґ–µ–љ–∞ –љ—Г–Љ–µ—А–∞—Ж–Є—П —А–Є—Б—Г–љ–Ї–Њ–≤, –ї–Є—В–µ—А–∞—В—Г—А—Л –Є –Є—Б—В–Њ—З–љ–Є–Ї–Њ–≤ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є, —Б—З–Є—В–∞—П —Б –њ–µ—А–≤–Њ–є —Б—В–∞—В—М–Є –Њ—В 17 –∞–≤–≥—Г—Б—В–∞ 2016 –≥–Њ–і–∞.
–Ъ–ї—О—З–µ–≤—Л–µ —Б–ї–Њ–≤–∞: –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–µ –∞–љ–∞–ї–Њ–≥–Є–Є; –Љ–љ–Њ–ґ–µ—Б—В–≤–∞; –љ–∞–≥–ї—П–і–љ—Л–µ –Љ–Њ–і–µ–ї–Є; –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ—Б—В—М; —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ–Њ—Б—В—М; —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В—М; —В–Њ—А; —В–Њ–Ї–∞–Љ–∞–Ї; —И–∞—А.
Keywords: ball; controllability; effectiveness; mathematical sets; mechanical analogies; predictability; visual models; tokamak; torus.
–Т –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ —Б—Г—Й–µ—Б—В–≤—Г—О—В —З–Є—Б–ї–Њ–≤—Л–µ –Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–µ –Њ—Б–Є [1, —Б 13, 14]. –Т –∞—Б—В—А–Њ–љ–Њ–Љ–Є–Є —Б—Г—Й–µ—Б—В–≤—Г—О—В –њ–Њ–Ј–љ–∞–≤–∞—В–µ–ї—М–љ—Л–µ –Љ–Њ–і–µ–ї–Є –і–≤–Є–ґ–µ–љ–Є—П –њ–ї–∞–љ–µ—В —Б–Њ–ї–љ–µ—З–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л [13] –Є –≥–∞–ї–∞–Ї—В–Є—З–µ—Б–Ї–Є—Е —Б—В—А—Г–Ї—В—Г—А [14]. –Т —Д–Є–Ј–Є–Ї–µ —Б—Г—Й–µ—Б—В–≤—Г—О—В: –њ–ї–∞–љ–µ—В–∞—А–љ–∞—П –Љ–Њ–і–µ–ї—М –∞—В–Њ–Љ–∞ –†–µ–Ј–µ—А—Д–Њ—А–і–∞ [15], –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л–µ –Љ–Њ–і–µ–ї–Є –Ї—А–Є—Б—В–∞–ї–ї–Є—З–µ—Б–Ї–Є—Е —А–µ—И—С—В–Њ–Ї [16], –∞–љ–∞–ї–Њ–≥–Є—П –Љ–µ–ґ–і—Г –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–Љ–Є –Є —Н–ї–µ–Ї—В—А–Њ–Љ–∞–≥–љ–Є—В–љ—Л–Љ–Є –Ї–Њ–ї–µ–±–∞–љ–Є—П–Љ–Є [17]. –Э–∞–≥–ї—П–і–љ—Л–µ –Љ–Њ–і–µ–ї–Є –Є –∞–љ–∞–ї–Њ–≥–Є–Є –Њ–±–ї–µ–≥—З–∞—О—В –Њ–±—К—П—Б–љ–µ–љ–Є–µ –Є –њ–Њ–љ–Є–Љ–∞–љ–Є–µ —Б–ї–Њ–ґ–љ—Л—Е –Ї–∞—В–µ–≥–Њ—А–Є–є, —А–∞–Ј–љ—Л—Е —П–≤–ї–µ–љ–Є–є, –њ–Њ–Ј–≤–Њ–ї—П—О—В –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞—В—М –њ—А–Њ—Ж–µ—Б—Б—Л, —Б–Њ–Ј–і–∞–≤–∞—В—М –љ–Њ–≤—Л–µ —В–µ—Е–љ–Њ–ї–Њ–≥–Є–Є, —Г—Б—В—А–Њ–є—Б—В–≤–∞, –Љ–∞—В–µ—А–Є–∞–ї—Л. –Т –Ї–∞—З–µ—Б—В–≤–µ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є—Е –∞–љ–∞–ї–Њ–≥–Є–є —Б—А–∞–≤–љ–Є–Љ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–µ —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В–Є —И–∞—А–∞ вАФ –Љ—П—З–∞ –Є —В–Њ—А–∞ вАФ –≥–Є–Љ–љ–∞—Б—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–±—А—Г—З–∞.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї—Г—О —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В—М —И–∞—А–∞. –†–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–љ—Л–µ –њ–Њ –≤–Є–і–∞–Љ, —А–∞–Ј–Љ–µ—А–∞–Љ, –Љ–∞—Б—Б–µ —И–∞—А—Л вАФ –Љ—П—З–Є –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –і–ї—П —Б–њ–Њ—А—В–Є–≤–љ—Л—Е —Б–Њ—А–µ–≤–љ–Њ–≤–∞–љ–Є–є, —Ж–Є—А–Ї–Њ–≤—Л—Е –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є, —А–∞–Ј–≤–ї–µ—З–µ–љ–Є–є, —Д–Є–Ј–Ї—Г–ї—М—В—Г—А–љ—Л—Е –Ј–∞–љ—П—В–Є–є –≤ –њ–Њ—Б—В–Њ—П–љ–љ–Њ–Љ –њ–Њ–ї–µ —Б–Є–ї—Л –Ј–µ–Љ–љ–Њ–≥–Њ –њ—А–Є—В—П–ґ–µ–љ–Є—П –њ—А–Є –∞—В–Љ–Њ—Б—Д–µ—А–љ–Њ–Љ –і–∞–≤–ї–µ–љ–Є–Є –≤–Њ–Ј–і—Г—Е–∞. –°–њ–Њ—А—В—Б–Љ–µ–љ—Л, —Ж–Є—А–Ї–Њ–≤—Л–µ –∞—А—В–Є—Б—В—Л, —Д–Є–Ј–Ї—Г–ї—М—В—Г—А–љ–Є–Ї–Є, —А–∞–Ј–≤–ї–µ–Ї–∞—О—Й–Є–µ—Б—П –≥—А–∞–ґ–і–∞–љ–µ –Њ—В—А–∞–±–∞—В—Л–≤–∞—О—В —Б—В–∞–љ–і–∞—А—В–љ—Л–µ –њ—А–Є—С–Љ—Л —Г–њ—А–∞–≤–ї–µ–љ–Є—П —И–∞—А–∞–Љ–Є вАФ –Љ—П—З–∞–Љ–Є, –њ—А–Є–Ї–ї–∞–і—Л–≤–∞—П –Ї –љ–Є–Љ —А–∞–Ј–љ—Л–µ —Б–Є–ї—Л –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П. –Ф–≤–Є–ґ–µ–љ–Є–µ —И–∞—А–Њ–≤ вАФ –Љ—П—З–µ–є –≤ –Є–≥—А–∞—Е —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ–µ, –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ–µ, —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ–Њ–µ. –Т–Њ–Ј–і—Г—И–љ–∞—П —Б—А–µ–і–∞, —В–≤—С—А–і—Л–µ –Њ–њ–Њ—А—Л, –Є–≥—А–Њ–≤—Л–µ –њ—А–µ–њ—П—В—Б—В–≤–Є—П –Њ–Ї–∞–Ј—Л–≤–∞—О—В —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–µ –і–≤–Є–ґ–µ–љ–Є—О. –°—В–∞–љ–і–∞—А—В–љ—Л–є —И–∞—А вАФ –Љ—П—З –Є–Љ–µ–µ—В —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–µ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Љ–∞—Б—Б—Л –њ–Њ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–Љ—Г –Њ–±—К—С–Љ—Г –≤–Њ–Ї—А—Г–≥ —Ж–µ–љ—В—А–∞ —В—П–ґ–µ—Б—В–Є, –Ї–Њ—В–Њ—А—Л–є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї –Љ–∞—В–µ—А–Є–∞–ї—М–љ–∞—П —В–Њ—З–Ї–∞ ¬ЂC¬ї (—А–Є—Б. 11) –≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е –Њ–њ–Є—Б–∞–љ–Є—П—Е —В—А–∞–µ–Ї—В–Њ—А–Є–є –µ–≥–Њ –і–≤–Є–ґ–µ–љ–Є—П, –Є–Ј—Г—З–∞–µ–Љ—Л—Е –≤ —Б—А–µ–і–љ–µ–є —И–Ї–Њ–ї–µ.

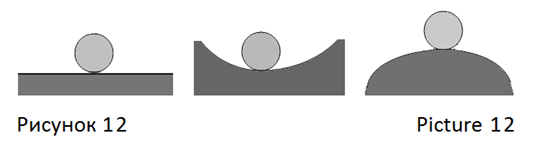
–°–Є–ї–∞ –≤–љ–µ—И–љ–µ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П F, –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–∞—П –Ї —Ж–µ–љ—В—А—Г —И–∞—А–∞ –°, —Б–Њ–Ј–і–∞–µ—В –µ–Љ—Г –њ–Њ—Б—В—Г–њ–∞—В–µ–ї—М–љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ. –°–Є–ї–∞ –≤–љ–µ—И–љ–µ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П F1, –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–∞—П –Љ–Є–Љ–Њ —Ж–µ–љ—В—А–∞ —И–∞—А–∞ —З–µ—А–µ–Ј –µ–≥–Њ –Њ–±—К—С–Љ, –Є–Љ–µ–µ—В –і–≤–µ —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є–µ: F —Б–Њ–Ј–і–∞–µ—В —И–∞—А—Г –њ–Њ—Б—В—Г–њ–∞—В–µ–ї—М–љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ, F2 —Б–Њ–Ј–і–∞–µ—В —И–∞—А—Г –≤—А–∞—Й–∞—В–µ–ї—М–љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ (—А–Є—Б. 11). –Т—Б–µ —В–Њ—З–Ї–Є –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Њ–±—Л—З–љ–Њ–≥–Њ —И–∞—А–∞ вАФ –Љ—П—З–∞ –Њ–і–Є–љ–∞–Ї–Њ–≤—Л –њ–Њ —А–µ–Ј—Г–ї—М—В–∞—В—Г –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П. –Я–ї–Њ—Й–∞–і—М –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П —А–∞–≤–љ–∞ –њ–ї–Њ—Й–∞–і–Є —Б—Д–µ—А—Л. –Ю—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П –Ї –њ–ї–Њ—Й–∞–і–Є —Б—Д–µ—А—Л —А–∞–≤–љ–Њ 1, –Є–ї–Є 100% вАФ —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–µ—В —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В—М —И–∞—А–∞ вАФ –Љ—П—З–∞ –Є —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –≤—А–µ–Љ–µ–љ–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П —И–∞—А–Њ–≤ вАФ –Љ—П—З–µ–є –≤ –Є–≥—А–µ –≤–Њ –Љ–љ–Њ–≥–Є—Е –≤–Є–і–∞—Е —Б–њ–Њ—А—В–∞ –Є —А–∞–Ј–≤–ї–µ—З–µ–љ–Є–є: 100%. –Ш—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ –≤ –Є–≥—А–∞—Е —И–∞—А–Њ–≤ вАФ –Љ—П—З–µ–є: –і–≤–Є–ґ–µ–љ–Є–µ –≤–Њ –≤—Б–µ—Е –њ–ї–Њ—Б–Ї–Њ—Б—В—П—Е. –Ґ–∞–Ї –ґ–µ –Є–Ј–≤–µ—Б—В–љ–Њ –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ–µ, –њ–Њ–≤—В–Њ—А—П–µ–Љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ –Є —Б–Њ—Б—В–Њ—П–љ–Є–µ —И–∞—А–∞ –љ–∞ –њ–ї–Њ—Б–Ї–Њ–є, –≤–Њ–≥–љ—Г—В–Њ–є –Є –≤—Л–њ—Г–Ї–ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—П—Е –≤ –≤–Є–і–∞—Е –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П: –±–µ–Ј—А–∞–Ј–ї–Є—З–љ–Њ–≥–Њ, —Г—Б—В–Њ–є—З–Є–≤–Њ–≥–Њ –Є –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ–≥–Њ (—А–Є—Б. 12), [18].
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї—Г—О —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В—М —В–Њ—А–∞. –Ф–ї—П —Б–њ–Њ—А—В–Є–≤–љ—Л—Е —Б–Њ—А–µ–≤–љ–Њ–≤–∞–љ–Є–є, —Ж–Є—А–Ї–Њ–≤—Л—Е –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є, —А–∞–Ј–≤–ї–µ—З–µ–љ–Є–є, —Д–Є–Ј–Ї—Г–ї—М—В—Г—А–љ—Л—Е –Ј–∞–љ—П—В–Є–є –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –≥–Є–Љ–љ–∞—Б—В–Є—З–µ—Б–Ї–Є–є –Њ–±—А—Г—З.
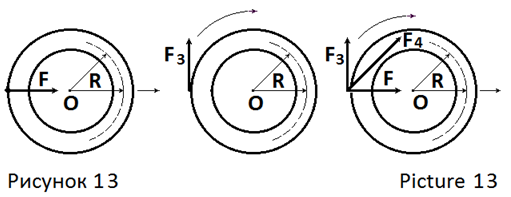
–¶–µ–љ—В—А —В—П–ґ–µ—Б—В–Є —В–Њ—А–∞ вАФ –Њ–±—А—Г—З–∞ –љ–∞—Е–Њ–і–Є—В—Б—П –≤–љ–µ –µ–≥–Њ –Њ–±—К—С–Љ–∞, –≤ –µ–≥–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–Љ —Ж–µ–љ—В—А–µ вАФ —В–Њ—З–Ї–µ –Ю (—А–Є—Б. 13, —А–Є—Б. 14). –Ф–Њ–њ—Г—Б—В–Є–Љ, –≤–µ–Ї—В–Њ—А—Л —Б–Є–ї –≤–љ–µ—И–љ–µ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П F, F3, F4 –љ–∞—Е–Њ–і—П—В—Б—П –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є R–ЮR, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —Ж–µ–љ—В—А –Ю —В–Њ—А–∞ вАФ –Њ–±—А—Г—З–∞ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –µ–≥–Њ –Њ—Б–Є. –Ґ–Њ–≥–і–∞ —Б–Є–ї–∞ F, –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–∞—П –Ї —Ж–µ–љ—В—А—Г –Њ–±—А—Г—З–∞, —Б–Њ–Ј–і–∞—Б—В –µ–Љ—Г –њ–Њ—Б—В—Г–њ–∞—В–µ–ї—М–љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ, —Б–Є–ї–∞ F3 вАФ –≤—А–∞—Й–∞—В–µ–ї—М–љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ. –Ю–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–µ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–µ —Б–Є–ї F –Є F3 (—А–∞–≤–љ–Њ–і–µ–є—Б—В–≤—Г—О—Й–∞—П F4) —Б–Њ–Ј–і–∞—Б—В –Њ–±—А—Г—З—Г –њ–Њ—Б—В—Г–њ–∞—В–µ–ї—М–љ–Њ вАФ –≤—А–∞—Й–∞—В–µ–ї—М–љ–Њ–µ –і–≤–Є–ґ–µ–љ–Є–µ –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є R–ЮR (—А–Є—Б. 13). –°–Є–ї–∞ –≤–љ–µ—И–љ–µ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П F5, –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–∞—П –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –Ї –њ–ї–Њ—Б–Ї–Њ—Б—В–Є R–ЮR, —Б–Њ–Ј–і–∞—Б—В –Њ–±—А—Г—З—Г ¬Ђ–Ї—Г–≤—Л—А–Ї–∞—О—Й–Є–є¬ї –Љ–Њ–Љ–µ–љ—В (—А–Є—Б 14). –°–Є–ї–∞ –≤–љ–µ—И–љ–µ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П F6, –Є–Љ–µ—П —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є–µ F5 –Є F, —Б–Њ–Ј–і–∞—Б—В —В–Њ—А—Г вАФ –Њ–±—А—Г—З—Г ¬Ђ–Ї—Г–≤—Л—А–Ї–∞—О—Й–µ–µ—Б—П¬ї –і–≤–Є–ґ–µ–љ–Є–µ —Б–Њ —Б–ї–Њ–ґ–љ—Л–Љ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–њ–Є—Б–∞–љ–Є–µ–Љ, —В–∞–Ї –Ї–∞–Ї –Њ–±—А—Г—З –љ–µ –Ј–∞–Љ–µ–љ—П–µ—В—Б—П –Њ–і–љ–Њ–є –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–Њ–є –Є–Ј вАФ –Ј–∞ –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–∞—Б—Б—Л –Њ–±—А—Г—З–∞ –њ–Њ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–Љ—Г –Њ–±—К—С–Љ—Г –≤–Њ–Ї—А—Г–≥ —Ж–µ–љ—В—А–∞ —В—П–ґ–µ—Б—В–Є. –Ґ–∞–Ї –ґ–µ —Б–ї–Њ–ґ–љ—Л–µ —Д–Њ—А–Љ—Л –і–≤–Є–ґ–µ–љ–Є—П –±—Г–і—Г—В –≤—Л–Ј—Л–≤–∞—В—М –≤–љ–µ—И–љ–Є–µ —Б–Є–ї—Л F7 вАФ F10 (—А–Є—Б. 14) –Є –≤—Б–µ –і—А—Г–≥–Є–µ —Б–Є–ї—Л, –≤–µ–Ї—В–Њ—А–∞ –Ї–Њ—В–Њ—А—Л—Е –љ–µ —А–∞—Б–њ–Њ–ї–∞–≥–∞—О—В—Б—П –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є R–ЮR.
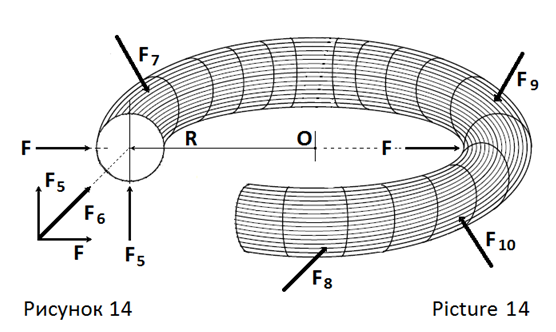
–Ґ–Њ—З–Ї–Є –љ–∞–і—С–ґ–љ–Њ —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ–≥–Њ, –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П –љ–∞ –Њ–±—А—Г—З —Б–Є–ї F, F3, F4 —А–∞—Б–њ–Њ–ї–∞–≥–∞—О—В—Б—П –љ–∞ –≤–љ–µ—И–љ–µ–є –Є –≤–љ—Г—В—А–µ–љ–љ–µ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—П—Е –Ї–Њ–ї—М—Ж–∞ –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є ROR (—А–Є—Б. 13). –Я–ї–Њ—Й–∞–і—М —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ–≥–Њ, –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ–≥–Њ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П —Б–Є–ї –љ–∞ —В–Њ—А вАФ –Њ–±—А—Г—З –Њ–њ—А–µ–і–µ–ї–Є—В—М —В—А—Г–і–љ–Њ. –Ю–љ–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –Є–љ–і–Є–≤–Є–і—Г–∞–ї—М–љ–Њ–є –і–ї—П –Є—Б–њ–Њ–ї–љ–Є—В–µ–ї—П —Г–њ—А–∞–ґ–љ–µ–љ–Є–є –Є –Њ–±—А—Г—З–∞. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ–љ–∞ –Љ–µ–љ—М—И–µ –њ–ї–Њ—Й–∞–і–Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —В–Њ—А–∞ вАФ –Њ–±—А—Г—З–∞. –Т—А–µ–Љ—П –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П –≥–Є–Љ–љ–∞—Б—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–±—А—Г—З–∞ –≤ –њ—А–Њ–≥—А–∞–Љ–Љ–∞—Е –њ–Њ —Е—Г–і–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є –≥–Є–Љ–љ–∞—Б—В–Є–Ї–µ: –Љ–µ–љ–µ–µ 30% [19], –њ—А–Є —Н—В–Њ–Љ –≤—А–µ–Љ—П –і–≤–Є–ґ–µ–љ–Є—П –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є R–ЮR –Є –≤—А–µ–Љ—П ¬Ђ–Ї—Г–≤—Л—А–Ї–∞—О—Й–µ–≥–Њ—Б—П¬ї –і–≤–Є–ґ–µ–љ–Є—П –њ–Њ–і –і–µ–є—Б—В–≤–Є–µ–Љ —Б–Є–ї F5 –Є F –і–µ–ї—П—В—Б—П –њ—А–Є–Љ–µ—А–љ–Њ –њ–Њ—А–Њ–≤–љ—Г —Г –≤–µ–і—Г—Й–Є—Е –Љ–∞—Б—В–µ—А–Њ–≤ —Е—Г–і–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є –≥–Є–Љ–љ–∞—Б—В–Є–Ї–Є [20].
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≥–µ–Њ–Љ–µ—В—А–Є—П —И–∞—А–Њ–≤ вАФ –Љ—П—З–µ–є —Б —Ж–µ–љ—В—А–Њ–Љ —В—П–ґ–µ—Б—В–Є –≤–љ—Г—В—А–Є –Њ–±—К—С–Љ–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В –Є—Е –±–Њ–ї—М—И—Г—О —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В—М, –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ—Б—В—М, —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ–Њ—Б—В—М –Є –њ—А–Є–Љ–µ–љ—П–µ–Љ–Њ—Б—В—М –≤ –Є–≥—А–∞—Е, —З–µ–Љ —В–Њ—А–∞ вАФ –Њ–±—А—Г—З–∞ —Б —Ж–µ–љ—В—А–Њ–Љ —В—П–ґ–µ—Б—В–Є –≤–љ–µ –Њ–±—К—С–Љ–∞ —В–Њ—А–∞.
–Ф–µ—В–∞–ї—М–љ–Њ–µ —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є–µ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В–Є –≥–Є–Љ–љ–∞—Б—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–±—А—Г—З–∞ –њ–Њ–Ј–≤–Њ–ї–Є—В –њ–Њ–љ—П—В—М –Є –Њ–±—К—П—Б–љ–Є—В—М —З–∞—Б—В—М —В—А—Г–і–љ–Њ—Б—В–µ–є –Є –Є–љ–ґ–µ–љ–µ—А–љ—Л—Е –њ—А–Њ–±–ї–µ–Љ —Б —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ—Б—В—М—О, —Б—В–∞–±–Є–ї—М–љ–Њ—Б—В—М—О –Є –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ—Б—В—М—О –њ–ї–∞–Ј–Љ—Л –≤ —В–Њ—А–Њ–Є–і–∞–ї—М–љ—Л—Е —Г—Б—В–∞–љ–Њ–≤–Ї–∞—Е —В–Є–њ–∞ —Б—В–µ–ї–ї–∞—А–∞—В–Њ—А, —В–Њ–Ї–∞–Љ–∞–Ї.
–Т –Ј–∞–Ї–ї—О—З–µ–љ–Є–Є –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–Є –Ї—А–∞—В–Ї–Њ –Њ—В–Љ–µ—В–Є–Љ –Њ–і–љ–Њ –Њ—З–µ–≤–Є–і–љ–Њ–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞: —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ –і–≤—Г—Е –Љ–љ–Њ–ґ–µ—Б—В–≤ –Ј–∞–Љ–Ї–љ—Г—В—Л—Е –ї–Є–љ–Є–є вАФ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є –Љ–∞–ї—Л—Е –Є –±–Њ–ї—М—И–Є—Е —А–∞–і–Є—Г—Б–Њ–≤ –≤ —А–∞–Ј–љ—Л—Е –њ–ї–Њ—Б–Ї–Њ—Б—В—П—Е –≤ –Њ–±—К—С–Љ–µ —В–Њ—А–∞. –≠—В–Є –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –Љ–Њ–ґ–љ–Њ –љ–∞–Ј–≤–∞—В—М –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л–Љ–Є, —А–∞–Ј–і–µ–ї—С–љ–љ—Л–Љ–Є ¬Ђ–і—Л—А–Ї–Њ–є¬ї —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞. –Ф–ї—П ¬Ђ–і—Л—А–Ї–Є¬ї —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞ –њ–Њ–і—Е–Њ–і–Є—В –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ ¬Ђ–њ—Г—Б—В–Њ–≥–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞¬ї –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ–±—К—С–Љ–∞ —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞ [1, —Б 8]. –Ґ–∞–Ї–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –Њ–±—К—С–Љ–∞ —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞ –њ—А–Є–≤–Њ–і–Є—В –Ї –і–≤—Г–Љ –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ—Л–Љ –ї–Њ–≥–Є—З–µ—Б–Ї–Є–Љ –≤–Њ–њ—А–Њ—Б–∞–Љ:
- –Ъ–∞–Ї–Є–µ —Б–ї–µ–і—Б—В–≤–Є—П –≤—Л—В–µ–Ї–∞—О—В –Є–Ј –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–≤–Њ–є—Б—В–≤–∞ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –і–≤—Г—Е –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –Љ–љ–Њ–ґ–µ—Б—В–≤ –Ј–∞–Љ–Ї–љ—Г—В—Л—Е –ї–Є–љ–Є–є –Є –Њ–і–љ–Њ–≥–Њ ¬Ђ–њ—Г—Б—В–Њ–≥–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞¬ї –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ–±—К—С–Љ–∞ —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞?
- –Ъ –Ї–∞–Ї–Є–Љ –≤—Л–≤–Њ–і–∞–Љ –њ—А–Є–≤–µ–і—С—В –і–µ—В–∞–ї—М–љ–Њ–µ —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–≤–Њ–є—Б—В–≤–∞ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –і–≤—Г—Е –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –Љ–љ–Њ–ґ–µ—Б—В–≤ –Ј–∞–Љ–Ї–љ—Г—В—Л—Е –ї–Є–љ–Є–є –Є ¬Ђ–њ—Г—Б—В–Њ–≥–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞¬ї —В–Њ—А–∞ вАФ –±—Г–±–ї–Є–Ї–∞ –њ—А–Є–Љ–µ–љ–Є—В–µ–ї—М–љ–Њ –Ї –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Њ–є —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є —А–µ–∞–Ї—Ж–Є–Є —Г–њ—А–∞–≤–ї—П–µ–Љ–Њ–≥–Њ —В–µ—А–Љ–Њ—П–і–µ—А–љ–Њ–≥–Њ —Б–Є–љ—В–µ–Ј–∞ –≤ —В–Њ—А–Њ–Є–і–∞–ї—М–љ—Л—Е –Њ–±—К—С–Љ–∞—Е —Г—Б—В–∞–љ–Њ–≤–Њ–Ї —В–Є–њ–∞ —В–Њ–Ї–∞–Љ–∞–Ї, —Б—В–µ–ї–ї–∞—А–∞—В–Њ—А?
–≠—В–Є –і–≤–∞ –≤–Њ–њ—А–Њ—Б–∞ –њ–Њ—А–Њ–ґ–і–∞—О—В –Љ–∞—Б—Б—Г —А–∞–Ј–љ–Њ–њ–ї–∞–љ–Њ–≤—Л—Е –∞—Б—Б–Њ—Ж–Є–∞—Ж–Є–є, –і–Њ–≥–∞–і–Њ–Ї, –і—А—Г–≥–Є—Е –≤–Њ–њ—А–Њ—Б–Њ–≤... –Р–≤—В–Њ—А—Г –љ–µ —Г–і–∞–ї–Њ—Б—М –љ–∞–є—В–Є –њ—А–Є–µ–Љ–ї–µ–Љ—Л—Е –Њ—В–≤–µ—В–Њ–≤ –і–Њ –Љ–Њ–Љ–µ–љ—В–∞ –њ—Г–±–ї–Є–Ї–∞—Ж–Є–Є –њ—А–µ–і–ї–∞–≥–∞–µ–Љ–Њ–є –≤–љ–Є–Љ–∞–љ–Є—О —З–Є—В–∞—В–µ–ї–µ–є –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–Є. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ, –Њ—В–≤–µ—В—Л –њ–Њ—П–≤—П—В—Б—П —Б —В–µ—З–µ–љ–Є–µ–Љ –≤—А–µ–Љ–µ–љ–Є...
–Я—А–Њ–і–Њ–ї–ґ–µ–љ–Є–µ —Б–ї–µ–і—Г–µ—В ...
–С–Њ—А–Є—Б –†–µ–≤–∞—И–Є–љ, 19 –і–µ–Ї–∞–±—А—П 2017 –≥–Њ–і–∞.
In mathematics, there are numeral scale and coordinate axes [1, p. 13, p. 14]. In astronomy, there are cognitive models of movements of the planets of the solar system [13] and galactic structures [14]. In physics, there are: planetary model of the atom [15], spatial models of crystal lattices [16], analogy between mechanical and electromagnetic oscillations [17]. Visual models do easy explanation and understanding of complex categories, various phenomena, allow us to model any processes, to create new technologies, devices, materials. Let make a comparison of mechanical controllability of ball and of gymnastic hoop вАФ Hula Hoop.
Consider the mechanical controllability of a ball. Any balls are used for sports competitions, circus performances, entertainment, physical Culture, in constant uniform field, the forces of gravity; at atmospheric air pressure. There are many kinds, sizes, masses of balls in different games. Athletes, circus performers, entertaining and citizens practice standard methods of controlling balls, attaching to them different forces of mechanical action. The movements of balls in games are controlled, predictable, productive, effectively. The air environment, solid supports, game obstacles do resistance to movement of ball in plying. A standard ball has the uniform mass distribution by spherical volume around the center of mass, which is a material point in the mathematical descriptions of the trajectories of its motion, studied at school. The force of external influence F, directed to the center of the ball C, do it forward motion. The force of external influence F1, directed not to the center of the ball C across it volume, consists of two components: F do it forward motion, F2 do for ball rotary motion (pic. 11). All impact points on the surface of the ball have the identical result of action. The area of the predicted impact is equal to the area of the sphere. The ratio of the area of the predicted impact to the area of the sphere is equal to 1, or 100% вАФ this is a characteristic of the controllability of a ball. The time of using balls in the game in many sports and entertainment: 100%. In games the balls move in all planes. There is also known the mechanical equilibrium: indifferent, stable and unstable of ball on a flat, concave and convex surface (pic. 12), [18].
Consider the mechanical controllability of a torus. The Hula Hoop is used for sports competitions, circus performances, entertainment, physical Culture. The center of mass of the torus вАФ hoop is outside its volume, in its geometric center вАФ point ¬ЂO¬ї (pic. 13, pic. 14).
Let us assume that the vectors of external forces F, F3, F4 are in the plane R–ЮR, which passes through the torus center ¬ЂO¬ї perpendicular to its axis. The force of external influence F, directed to the center of the torus вАФ Hula Hoop ¬ЂO¬ї, do it forward motion; the force F3 do for Hula Hoop rotary motion. Impact of forces F and F3 (resultant F4) do for torus вАФ hoop forward вАФ rotary motion in the ROR plane (pic. 13). The force of external influence F5, directional perpendicular to the ROR plane, do for torus вАФ hoop ¬Ђsomersault¬ї moment (pic. 14). The force of external influence F6 (components F and F5) do for torus вАФ hoop ¬Ђsomersault¬ї movement with a complex mathematical description, because torus have uneven distribution of mass around the center of mass (unlike a ball) and torus is not replaced by a single material point. Points of controlled, predictable influence on the hoop of forces F, F3, F4 are located on the outer and inner circumferences of ring in the ROR plane (pic. 13). Area of controlled, predictable impact of forces on the torus-hoop is difficult to determine. This area can be individual for performer of exercises and hoop. Obviously, it is smaller than the area of surface of the torus-hoop. The time of using the gymnastic hoop in art gymnastics programs: less than 30% [19]. The time of movement in the ROR plane and time of ¬Ђsomersault¬ї movement almost equal at the competitions of the leading masters of art gymnastics [20].
Consequently, the geometry of the balls with the center of mass inside the volume determines their greater controllability, predictability, effectiveness, applicability and playability in games, than a torus вАФ hoop with a center of mass outside the volume of the torus.
Detailed consideration of mechanical controllability of the torus-hoop will understand and explain some of the difficulties and engineering problems with controllability, stability and predictability of plasma in toroidal installations of the type stellarator, tokamak.
In the conclusion of the second article briefly note one obvious mathematical property of a torus вАФ hoop: the existence of two sets of closed lines вАФ circles of small and large radii in different planes in the volume of the torus. These sets can be called independent and they are separated by ¬Ђhole¬ї of a torus вАФ hoop. The ¬Ђhole¬ї of a torus can be called an ¬Ђempty set¬ї relative to the volume of the torus [1, p. 8]. This representation of the volume of the torus leads to two logical questions:
1. What consequences follow from the mathematical property of the existence of two independent sets of closed lines and one ¬Ђempty set¬ї relative to the torus volume?
2. To what conclusions will the detailed consideration of the mathematical property of the existence of two independent sets of closed lines and the ¬Ђempty set¬ї of the torus-hoop apply to the practical realization of the reaction of controlled thermonuclear fusion in toroidal volumes of installations such as tokamak, stellarator?
These two questions give rise to a multitude of diverse associations, conjectures, other questions... The author does not have answers to these questions today. Perhaps the answers will appear over time...
To be continued ...
This translation was made by https://translate.google.ru//
Boris Revashin, December 19, 2017.
–Ы–Є—В–µ—А–∞—В—Г—А–∞, –Є—Б—В–Њ—З–љ–Є–Ї–Є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є / Literature, sources of information:
1. –§—А–Њ–ї–Њ–≤ –Э. –Р. –Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ –Є –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ –Є—Б—З–Є—Б–ї–µ–љ–Є–µ. –Ь., 1955. 339 —Б.
.....
13. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: http://spacegid.com/kompyuternaya-model-solnechnoy-sistemyi.html
14. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: http://spacegid.com/mlechnyiy-put.html
15. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: https://ru.wikipedia.org/wiki/–Я–ї–∞–љ–µ—В–∞—А–љ–∞—П_–Љ–Њ–і–µ–ї—М_–∞—В–Њ–Љ–∞
16. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: https://yandex.ru/images/search?text=–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л–µ_–Љ–Њ–і–µ–ї–Є_–Ї—А–Є—Б—В–∞–ї–ї–Є—З–µ—Б–Ї–Є—Е_—А–µ—И—С—В–Њ–Ї&stype=image&lr=
17. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: https://sites.google.com/site/mehielektromagnkolebania/teoria
18. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: http://fphysics.com/vidy_ravnovesiya
19. –°—В—А–∞–љ–Є—Ж–∞ —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: https://ru.wikipedia.org/wiki/–•—Г–і–Њ–ґ–µ—Б—В–≤–µ–љ–љ–∞—П_–≥–Є–Љ–љ–∞—Б—В–Є–Ї–∞
20. –°—В—А–∞–љ–Є—Ж—Л —Б–∞–є—В–∞ –≤ —Б–µ—В–Є –Є–љ—В–µ—А–љ–µ—В: www.youtube.com/=–•—Г–і–Њ–ґ–µ—Б—В–≤–µ–љ–љ–∞—П_–≥–Є–Љ–љ–∞—Б—В–Є–Ї–∞;









