Срочная публикация научной статьи
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
Исследование функциональных возможностей асимметричных алгоритмов шифроования
Рубрика: Физико-математические науки
Журнал: «Евразийский Научный Журнал №8 2015» (август 2015)
Количество просмотров статьи: 3272
Показать PDF версию Исследование функциональных возможностей асимметричных алгоритмов шифроования
Орлов Павел Олегович
магистр «НИУ ИТМО»
г. Санкт-Петербург
Аннотация: в статье описана обобщенная математическая модель для исследования функциональных возможностей асимметричных алгоритмов шифрования. В качестве примера возьмем криптоалгоритмы RSA и Elgamal. Данная статья будет полезна для выбора асимметричного криптоалгоритма в прикладной практике исходя из исследованных функциональных возможностей.
Ключевые слова: криптография, криптографические системы с открытым ключом, криптографические средства защиты информации, уязвимость, угроза, электронная цифровая подпись, криптографический ключ.
Разработанная для исследования математическая модель может быть использована в качестве основы при проектировании более совершенных криптосистем в будущем, которые предназначены для шифрования и расшифрования конфиденциальной и любой другой информации.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Разрабатываемая модель предназначена для исследования функциональных возможностей асимметричных криптосистем.
Для начала необходимо задать общее исходное описание модели.
K - Пространство ключей;
C - Пространство шифртекстов;
М - Пространство сообщений;
e и d - Ключ шифрования и расшифрования соответственно;
![]() - Функция шифрования для произвольного ключа
- Функция шифрования для произвольного ключа ![]() , такая что
, такая что ![]() ;
;
![]() - Функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифртекст c:
- Функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифртекст c: ![]() ;
;
![]() и
и ![]()
![]() - Набор для шифрования;
- Набор для шифрования;
![]() - Соответствующий набор для расшифрования;
- Соответствующий набор для расшифрования;
Каждая пара ![]() имеет свойство:
имеет свойство:
Если известно ![]() , невозможно решить уравнение
, невозможно решить уравнение ![]() . Отсюда следует, что по данному e невозможно определить ключ расшифрования d.
. Отсюда следует, что по данному e невозможно определить ключ расшифрования d.
Вся модель состоит из четырех элементов:
- Генерация ключей;
- Аутентичный канал передачи открытых ключей по открытому каналу;
- Шифрование;
- Расшифрование.
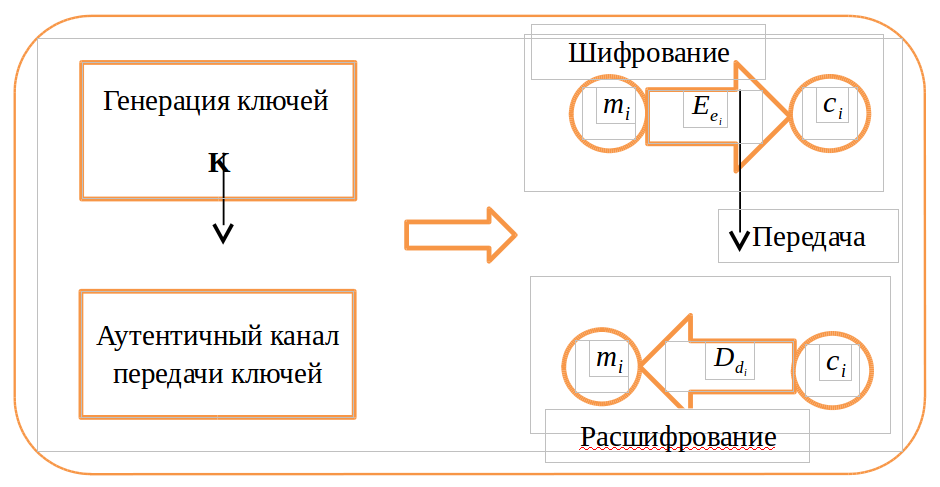
Рисунок 1 - Общая схема модели
ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ
Ссылаясь на обобщенную модель, были изучены функциональные возможности асимметричных криптоалгоритмов. Каждый из двух алгоритмов может быть использован не только для решения классической задачи криптографии, то есть для шифрования и расшифрования, но и для электронной цифровой подписи. Размер ключа каждого алгоритма может достигать 4096 бит. Была проанализирована скорость шифрования. Скорость полностью зависит от входных параметров алгоритма. Исходя из модели, скорость работы алгоритма El-Gamal медленнее, чем у алгоритма RSA. Криптостойкость работы алгоритма El-Gamal выше, чем у RSA, потому что криптосистема El-Gamal является асимметричным вероятностным алгоритмом шифрования и чем больше значений рандомизатора, тем лучше.
Рассмотренные алгоритмы обладают следующими функциональными возможностями: решают задачу ключевого управления (отсутствует обмен секретами между участниками защищенного взаимодействия), обеспечивают невозможность отказа от авторства и обеспечивают контроль целостности электронных документов, благодаря возможности реализации механизма ЭЦП.
Основным недостатком являются высокие вычислительные затраты, если сравнивать с симметричными криптоалгоритмами.
Список использованных источников
- Бутакова Н.Г.,Семененко В.А., Федоров Н.В. Криптографическая защита информации: учебное пособие для вузов. – М. : Изд-во МГИУ, 2011 . – 316 с. – ISBN 978-5-2760-1503-3.
- Алгоритмы: построение и анализ, 2-е издание. :Пер с англ. - М.: Издательский дом «Вильямс» ISBN 5-8459-0857-4 (рус.)
- В.Г.Потемкин "Введение в Matlab".
- ГОСТ 28147-89 — советский и российский стандарт симметричного шифрования, введённый в 1990 году, также является стандартом СНГ.









