–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–§—А–∞–Ї—В–∞–ї—М–љ–∞—П –Њ–±—А–∞–±–Њ—В–Ї–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є
–†—Г–±—А–Є–Ї–∞: –Ґ–µ—Е–љ–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ5 2017» (–Љ–∞–є, 2017)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 4624
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –§—А–∞–Ї—В–∞–ї—М–љ–∞—П –Њ–±—А–∞–±–Њ—В–Ї–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є
–°–Є–і–љ–µ–≤ –Р–љ–і—А–µ–є –Р–љ–і—А–µ–µ–≤–Є—З
—Б—В—Г–і–µ–љ—В –Љ–∞–≥–Є—Б—В—А–∞—В—Г—А—Л,
–§–µ–і–µ—А–∞–ї—М–љ–Њ–µ –≥–Њ—Б—Г–і–∞—А—Б—В–≤–µ–љ–љ–Њ–µ –±—О–і–ґ–µ—В–љ–Њ–µ –Њ–±—А–∞–Ј–Њ–≤–∞—В–µ–ї—М–љ–Њ–µ
—Г—З—А–µ–ґ–і–µ–љ–Є–µ –≤—Л—Б—И–µ–≥–Њ –њ—А–Њ—Д–µ—Б—Б–Є–Њ–љ–∞–ї—М–љ–Њ–≥–Њ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П
–Ь–Њ—Б–Ї–Њ–≤—Б–Ї–Є–є —В–µ—Е–љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В,
–≥. –Ь–Њ—Б–Ї–≤–∞
E-mail: sidnev38@gmail.com
–Р–љ–љ–Њ—В–∞—Ж–Є—П.
–Т –і–∞–љ–љ–Њ–є —Б—В–∞—В—М–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В—Б—П –Ј–∞–і–∞—З–∞, —Б–≤—П–Ј–∞–љ–љ–∞—П —Б —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–є –Њ–±—А–∞–±–Њ—В–Ї–Њ–є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є, —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–µ–Љ —В–µ—Б—В–Њ–≤—Л—Е –Њ–±—А–∞–Ј–Њ–≤, –њ—А–Є–≤–µ–і–µ–љ–∞ –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П —Д—А–∞–Ї—В–∞–ї–Њ–≤.
–Ъ–ї—О—З–µ–≤—Л–µ —Б–ї–Њ–≤–∞: —Д—А–∞–Ї—В–∞–ї—Л, —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–µ –Њ–±—А–∞–Ј–Њ–≤, —Д—А–∞–Ї—В–∞–ї—М–љ–∞—П –Њ–±—А–∞–±–Њ—В–Ї–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є, –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П —Д—А–∞–Ї—В–∞–ї–Њ–≤.
–Т–≤–µ–і–µ–љ–Є–µ.
–°—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ —В–µ–Њ—А–Є–Є —Д—А–∞–Ї—В–∞–ї–Њ–≤ вАФ —П—А–Ї–Є–є –њ—А–Є–Љ–µ—А —А–∞–Ј–≤–Є—В–Є—П –љ–Њ–≤–Њ–≥–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П –љ–∞—Г–Ї–Є, –≤ —А–∞–≤–љ–Њ–є –Љ–µ—А–µ –Њ—Б–љ–Њ–≤–∞–љ–љ–Њ–≥–Њ –Ї–∞–Ї –љ–∞ –і–Њ—Б—В–Є–ґ–µ–љ–Є—П—Е –≤ –≤–µ—Б—М–Љ–∞ –∞–±—Б—В—А–∞–Ї—В–љ—Л—Е –Њ–±–ї–∞—Б—В—П—Е –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є, —В–∞–Ї –Є –љ–∞ –љ–Њ–≤–Њ–Љ –≤–Ј–≥–ї—П–і–µ –љ–∞ –і–∞–≤–љ–Њ –Є–Ј–≤–µ—Б—В–љ—Л–є —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є–є –Љ–∞—В–µ—А–Є–∞–ї, –Ї–Њ—В–Њ—А—Л–є –і–Њ —Б–Њ–Ј–і–∞–љ–Є—П –∞–і–µ–Ї–≤–∞—В–љ—Л—Е —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є—Е –Љ–Њ–і–µ–ї–µ–є –љ–µ –њ–Њ–і–і–∞–≤–∞–ї—Б—П –љ–∞—Г—З–љ–Њ–Љ—Г –Њ–њ–Є—Б–∞–љ–Є—О –Є –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–Є.
–Э–∞—Г–Ї–∞ –Њ —Д—А–∞–Ї—В–∞–ї–∞—Е –Љ–Њ–ї–Њ–і–∞ –Є –±—Г—А–љ–Њ —А–∞–Ј–≤–Є–≤–∞–µ—В—Б—П, –љ–Њ –љ–µ –≤—Б–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Њ —Д—А–∞–Ї—В–∞–ї–∞—Е —Б–ї–Њ–ґ–Є–ї–Є—Б—М, –Є–Љ–µ—О—В—Б—П –µ—Й–µ —Б–њ–Њ—А–љ—Л–µ –Љ–Њ–Љ–µ–љ—В—Л. –Ю–і–љ–∞–Ї–Њ –Ј–∞–і–∞—З–∞ —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–є –Њ–±—А–∞–±–Њ—В–Ї–Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В –±–Њ–ї—М—И–Њ–є –Є–љ—В–µ—А–µ—Б –Ї–∞–Ї —Б –љ–∞—Г—З–љ–Њ–є, —В–∞–Ї –Є —Б –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Њ–є —В–Њ—З–µ–Ї –Ј—А–µ–љ–Є—П. –Я—А–Є–Љ–µ–љ–µ–љ–Є–µ —В–µ–Њ—А–Є–Є —Д—А–∞–Ї—В–∞–ї–Њ–≤ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Њ—В–Ї—А—Л—В—М –Њ–≥—А–Њ–Љ–љ—Л–µ –љ–µ–Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Л–µ —А–∞–љ–µ–µ —А–µ–Ј–µ—А–≤—Л –Є –њ—А–Є–Љ–µ–љ–Є—В—М –Є—Е, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –≤ –Њ–±–ї–∞—Б—В–Є —А–∞–Ј–ї–Є—З–љ—Л—Е —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –њ—А–Є–ї–Њ–ґ–µ–љ–Є–є.
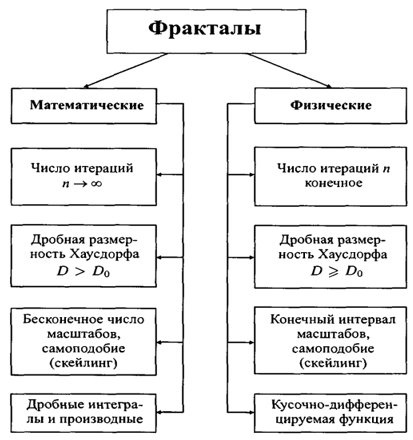
–Ъ–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П —Д—А–∞–Ї—В–∞–ї–Њ–≤.
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Д—А–∞–Ї—В–∞–ї—Л вАФ —Б–∞–Љ—Л–µ –љ–∞–≥–ї—П–і–љ—Л–µ —Д—А–∞–Ї—В–∞–ї—Л, –≤ –і–≤—Г—Е–Љ–µ—А–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Є—Е –њ–Њ–ї—Г—З–∞—О—В —Б –њ–Њ–Љ–Њ—Й—М—О –ї–Њ–Љ–∞–љ–Њ–є (–Є–ї–Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≤ —В—А–µ—Е–Љ–µ—А–љ–Њ–Љ —Б–ї—Г—З–∞–µ), –љ–∞–Ј—Л–≤–∞–µ–Љ–Њ–є –≥–µ–љ–µ—А–∞—В–Њ—А–Њ–Љ. –Ч–∞ –Њ–і–Є–љ —И–∞–≥ –∞–ї–≥–Њ—А–Є—В–Љ–∞ –Ї–∞–ґ–і—Л–є –Є–Ј –Њ—В—А–µ–Ј–Ї–Њ–≤, —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є—Е –ї–Њ–Љ–∞–љ—Г—О, –Ј–∞–Љ–µ–љ—П–µ—В—Б—П –љ–∞ –ї–Њ–Љ–∞–љ—Г—О-–≥–µ–љ–µ—А–∞—В–Њ—А –≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–Љ –Љ–∞—Б—И—В–∞–±–µ. –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–≥–Њ –њ–Њ–≤—В–Њ—А–µ–љ–Є—П —Н—В–Њ–є –њ—А–Њ—Ж–µ–і—Г—А—Л –њ–Њ–ї—Г—З–∞–µ—В—Б—П –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Д—А–∞–Ї—В–∞–ї.
–Р–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є–µ —Д—А–∞–Ї—В–∞–ї—Л вАФ –њ–Њ–ї—Г—З–∞—О—В –Є—Е —Б –њ–Њ–Љ–Њ—Й—М—О –љ–µ–ї–Є–љ–µ–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –≤ n-–Љ–µ—А–љ—Л—Е –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞—Е. –Э–∞–Є–±–Њ–ї–µ–µ –Є–Ј—Г—З–µ–љ—Л –і–≤—Г—Е–Љ–µ—А–љ—Л–µ –њ—А–Њ—Ж–µ—Б—Б—Л. –Ш–љ—В–µ—А–њ—А–µ—В–Є—А—Г—П –љ–µ–ї–Є–љ–µ–є–љ—Л–є –Є—В–µ—А–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Њ—Ж–µ—Б—Б, –Ї–∞–Ї –і–Є—Б–Ї—А–µ—В–љ—Г—О –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї—Г—О —Б–Є—Б—В–µ–Љ—Г, –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П —В–µ—А–Љ–Є–љ–Њ–ї–Њ–≥–Є–µ–є —В–µ–Њ—А–Є–Є —Н—В–Є—Е —Б–Є—Б—В–µ–Љ: —Д–∞–Ј–Њ–≤—Л–є –њ–Њ—А—В—А–µ—В, —Г—Б—В–∞–љ–Њ–≤–Є–≤—И–Є–є—Б—П –њ—А–Њ—Ж–µ—Б—Б, –∞—В—В—А–∞–Ї—В–Њ—А.
–°—В–Њ—Е–∞—Б—В–Є—З–µ—Б–Ї–Є–µ —Д—А–∞–Ї—В–∞–ї—Л вАФ –њ–Њ–ї—Г—З–∞—О—В—Б—П –≤ —В–Њ–Љ —Б–ї—Г—З–∞–µ, –µ—Б–ї–Є –≤ –Є—В–µ—А–∞—Ж–Є–Њ–љ–љ–Њ–Љ –њ—А–Њ—Ж–µ—Б—Б–µ —Е–∞–Њ—В–Є—З–µ—Б–Ї–Є –Љ–µ–љ—П—В—М –Ї–∞–Ї–Є–µ-–ї–Є–±–Њ –µ–≥–Њ –њ–∞—А–∞–Љ–µ—В—А—Л. –Я—А–Є —Н—В–Њ–Љ –њ–Њ–ї—Г—З–∞—О—В—Б—П –Њ–±—К–µ–Ї—В—Л –Њ—З–µ–љ—М –њ–Њ—Е–Њ–ґ–Є–µ –љ–∞ –њ—А–Є—А–Њ–і–љ—Л–µ вАФ –љ–µ—Б–Є–Љ–Љ–µ—В—А–Є—З–љ—Л–µ –і–µ—А–µ–≤—М—П, –Є–Ј—А–µ–Ј–∞–љ–љ—Л–µ –±–µ—А–µ–≥–Њ–≤—Л–µ –ї–Є–љ–Є–Є –Є —В.–і. –Ф–≤—Г–Љ–µ—А–љ—Л–µ —Б—В–Њ—Е–∞—Б—В–Є—З–µ—Б–Ї–Є–µ —Д—А–∞–Ї—В–∞–ї—Л –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –њ—А–Є –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–Є —А–µ–ї—М–µ—Д–∞ –Љ–µ—Б—В–љ–Њ—Б—В–Є –Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Љ–Њ—А—П .
–°—Г—Й–µ—Б—В–≤—Г—О—В –Є –і—А—Г–≥–Є–µ –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є —Д—А–∞–Ї—В–∞–ї–Њ–≤, –љ–∞–њ—А–Є–Љ–µ—А –і–µ–ї–µ–љ–Є–µ —Д—А–∞–Ї—В–∞–ї–Њ–≤ –љ–∞ –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л–µ (–∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є–µ –Є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ) –Є –љ–µ–і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л–µ (—Б—В–Њ—Е–∞—Б—В–Є—З–µ—Б–Ї–Є–µ).
–Я—А–Є–Љ–µ–љ–µ–љ–Є–µ —Д—А–∞–Ї—В–∞–ї–Њ–≤.
–Т–Њ-–њ–µ—А–≤—Л—Е, —Н—В–Њ —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–µ —Б–ґ–∞—В–Є–µ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є, –Є –≤–Њ-–≤—В–Њ—А—Л—Е –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –ї–∞–љ–і—И–∞—Д—В–Њ–≤, –і–µ—А–µ–≤—М–µ–≤, —А–∞—Б—В–µ–љ–Є–є –Є –≥–µ–љ–µ—А–Є—А–Њ–≤–∞–љ–Є–µ —Д—А–∞–Ї—В–∞–ї—М–љ—Л—Е —В–µ–Ї—Б—В—Г—А. –Ґ–∞–Ї–ґ–µ —Д—А–∞–Ї—В–∞–ї—Л –њ—А–Є–Љ–µ–љ—П—О—В—Б—П –≤ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –Я—А–Є –њ–Њ–Љ–Њ—Й–Є —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є –Љ–Њ–ґ–µ–Љ —Б–Є–ї—М–љ–Њ —Г–Љ–µ–љ—М—И–Є—В—М —А–∞–Ј–Љ–µ—А —Д–∞–є–ї–∞. –Т –Љ–µ—Е–∞–љ–Є–Ї–µ –Є —Д–Є–Ј–Є–Ї–µ —Д—А–∞–Ї—В–∞–ї—Л –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –±–ї–∞–≥–Њ–і–∞—А—П —Г–љ–Є–Ї–∞–ї—М–љ–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г –њ–Њ–≤—В–Њ—А—П—В—М –Њ—З–µ—А—В–∞–љ–Є—П –Љ–љ–Њ–≥–Є—Е –Њ–±—К–µ–Ї—В–Њ–≤ –њ—А–Є—А–Њ–і—Л. –§—А–∞–Ї—В–∞–ї—Л –њ–Њ–Ј–≤–Њ–ї—П—О—В –њ—А–Є–±–ї–Є–ґ–∞—В—М –і–µ—А–µ–≤—М—П, –≥–Њ—А–љ—Л–µ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є —В—А–µ—Й–Є–љ—Л —Б –±–Њ–ї–µ–µ –≤—Л—Б–Њ–Ї–Њ–є —В–Њ—З–љ–Њ—Б—В—М—О, —З–µ–Љ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є—П –љ–∞–±–Њ—А–∞–Љ–Є –Њ—В—А–µ–Ј–Ї–Њ–≤ –Є–ї–Є –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤.
–†–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–µ –Њ–±—А–∞–Ј–Њ–≤.
–†–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–µ –Њ–±—А–∞–Ј–Њ–≤ –Њ—В–Њ–ґ–і–µ—Б—В–≤–ї—П–µ—В—Б—П —Б –≤—Л—П—Б–љ–µ–љ–Є–µ–Љ –≤–Њ–њ—А–Њ—Б–∞ –Њ —В–Њ–Љ, –Ї –Ї–∞–Ї–Њ–Љ—Г –Ї–ї–∞—Б—Б—Г –Њ–±—К–µ–Ї—В–Њ–≤ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ—В–љ–µ—Б–µ–љ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–µ–Љ—Л–є –Њ–±—К–µ–Ї—В. –Ю—В–Љ–µ—В–Є–Љ, —З—В–Њ –њ—А–Њ–±–ї–µ–Љ–∞ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –Њ—Е–≤–∞—В—Л–≤–∞–µ—В —И–Є—А–Њ–Ї–Є–є –Ї—А—Г–≥ –Ј–∞–і–∞—З. –≠—В–Њ –Є –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –∞–ї—Д–∞–≤–Є—В–∞ –Ї–ї–∞—Б—Б–Њ–≤ –Є —Б–ї–Њ–≤–∞—А—П –њ—А–Є–Ј–љ–∞–Ї–Њ–≤, –∞ —В–∞–Ї–ґ–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Є –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П, –Є –Љ–µ—В–Њ–і—Л –Њ–±—А–∞–±–Њ—В–Ї–Є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є. –Э–∞ –њ—А–∞–Ї—В–Є–Ї–µ —Б–њ–µ—Ж–Є—Д–Є–Ї–∞ –ї—О–±–Њ–є –Ј–∞–і–∞—З–Є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —В–Є–њ–Њ–Љ –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є. –†–∞–±–Њ—З–Є–є —Б–ї–Њ–≤–∞—А—М –њ—А–Є–Ј–љ–∞–Ї–Њ–≤ –њ—А–Є —А–∞–і–Є–Њ–ї–Њ–Ї–∞—Ж–Є–Њ–љ–љ–Њ–Љ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–Є –≤—Б–µ–≥–і–∞ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В —Б–Є–≥–љ–∞—В—Г—А—Л. –Ю–љ–Є –≤–Ї–ї—О—З–∞—О—В –≤ —Б–µ–±—П –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Г—О, –≤—А–µ–Љ–µ–љ–љ—Г—О, —Б–њ–µ–Ї—В—А–∞–ї—М–љ—Г—О –Є –њ–Њ–ї—П—А–Є–Ј–∞—Ж–Є–Њ–љ–љ—Г—О —Б—В—А—Г–Ї—В—Г—А—Г –Њ—В—А–∞–ґ–µ–љ–љ—Л—Е —Б–Є–≥–љ–∞–ї–Њ–≤, –љ–µ —Б–≤—П–Ј–∞–љ–љ—Л–µ –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ —Б –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –Њ–±—К–µ–Ї—В–Њ–≤ —А–∞–і–Є–Њ–ї–Њ–Ї–∞—Ж–Є–Є. –Ю–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ–µ —А–µ—И–µ–љ–Є–µ –Њ —Б–Њ—Б—В–∞–≤–µ —А–∞–±–Њ—З–µ–≥–Њ —Б–ї–Њ–≤–∞—А—П –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Є–љ—П—В–Њ –≤–љ–µ –Ј–∞–і–∞—З–Є –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є –Њ–±—К–µ–Ї—В–Њ–≤, –Ї–Њ–≥–і–∞ –Є—Е –њ–Њ–і—А–∞–Ј–і–µ–ї—П—О—В –љ–∞ –Ї–ї–∞—Б—Б—Л. –Ч–∞–і–∞—З–Є –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –∞–ї—Д–∞–≤–Є—В–∞ –Ї–ї–∞—Б—Б–Њ–≤ –Є —Б–ї–Њ–≤–∞—А—П –њ—А–Є–Ј–љ–∞–Ї–Њ–≤ –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ —Б–≤—П–Ј–∞–љ—Л —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —В–µ—Е –Є–ї–Є –і—А—Г–≥–Є—Е —А–µ—И–∞—О—Й–Є—Е –њ—А–∞–≤–Є–ї-–∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –Є —Б–µ–ї–µ–Ї—Ж–Є–Є. –Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –њ—А–µ–і–ї–Њ–ґ–µ–љ –љ–Њ–≤—Л–є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л–є –њ–Њ–і—Е–Њ–і –Ї —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—О –Њ–±—А–∞–Ј–Њ–≤ —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –њ–Њ–љ—П—В–Є–є —В–Њ–њ–Њ–ї–Њ–≥–Є–Є –≤—Л–±–Њ—А–Ї–Є —Б–Є–≥–љ–∞–ї–Њ–≤ –Є–ї–Є –њ–Њ–ї–µ–є –Є —Д—А–∞–Ї—В–∞–ї—М–љ—Л—Е –њ—А–Є–Љ–Є—В–Є–≤–Њ–≤.
–§—А–∞–Ї—В–∞–ї—М–љ–∞—П –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П –Є –Ї–ї–∞—Б—В–µ—А–Є–Ј–∞—Ж–Є—П –Њ–±—К–µ–Ї—В–Њ–≤.
–Ъ–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П вАФ —Н—В–Њ —Г–њ–Њ—А—П–і–Њ—З–µ–љ–Є–µ –Њ–±—К–µ–Ї—В–Њ–≤ –њ–Њ –Є—Е —Б—Е–Њ–ґ–µ—Б—В–Є, –≤–Ї–ї—О—З–∞—П –њ—А–Њ—Ж–µ—Б—Б—Л –Є –і–µ–є—Б—В–≤–Є—П. –Ю–±—Й–∞—П –њ–Њ—Б—В–∞–љ–Њ–≤–Ї–∞ –Ј–∞–і–∞—З–Є –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є —П–≤–ї—П–µ—В—Б—П —Б—В–Њ—Е–∞—Б—В–Є—З–µ—Б–Ї–Њ–є, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –≤–µ–Ї—В–Њ—А—Л –њ—А–Є–Ј–љ–∞–Ї–Њ–≤ –Є–Ј-–Ј–∞ —И—Г–Љ–Њ–≤ –Є –њ–Њ–Љ–µ—Е –≤—Б–µ–≥–і–∞ –Њ–±–ї–∞–і–∞—О—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ—Л–Љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ.
–Х—Б–ї–Є –љ–∞ –Њ–њ—В–Є—З–µ—Б–Ї–Њ–Љ –Є–ї–Є —А–∞–і–Є–Њ–ї–Њ–Ї–∞—Ж–Є–Њ–љ–љ–Њ–Љ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–Є –њ—А–Є—Б—Г—В—Б—В–≤—Г—О—В —А–∞–Ј–ї–Є—З–љ—Л–µ –Њ–±—К–µ–Ї—В—Л –Є —Д–Њ–љ–Њ–≤—Л–µ –њ–Њ–Љ–µ—Е–Є, —В–Њ –≤–µ–Ї—В–Њ—А—Л –і–µ—Б–Ї—А–Є–њ—В–Њ—А–Њ–≤ –≥—А—Г–њ–њ–Є—А—Г—О—В—Б—П –Њ–Ї–Њ–ї–Њ —Б–Є–≥–љ–∞—В—Г—А –Њ–±—К–µ–Ї—В–Њ–≤, –Њ—Б—В–∞–≤–ї—П—П —Б–ї–∞–±–Њ –Ј–∞–њ–Њ–ї–љ–µ–љ–љ—Л–Љ —А–∞–Ј–і–µ–ї—П—О—Й–µ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –Ј–∞–і–∞—З–∞ –Ї–ї–∞—Б—В–µ—А–Є–Ј–∞—Ж–Є–Є вАФ —А–∞–Ј–±–Є–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –Є—Б—Е–Њ–і–љ–Њ–≥–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –љ–∞ –Ї–ї–∞—Б—Б—Л –њ–Њ —В–Њ–Љ—Г –Є–ї–Є –Є–љ–Њ–Љ—Г –Ї—А–Є—В–µ—А–Є—О –±–ї–Є–Ј–Њ—Б—В–Є –Є–ї–Є —Б—Е–Њ–і—Б—В–≤–∞. –†–∞–Ј–Љ–µ—А—Л –Ї–ї–∞—Б—В–µ—А–Њ–≤ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –і–µ—Б–Ї—А–Є–њ—В–Њ—А–Њ–≤ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П –Ј–∞–і–∞–љ–љ–Њ–є –Љ–µ—А–Њ–є —Б—Е–Њ–і—Б—В–≤–∞ –њ—А–Є–Ј–љ–∞–Ї–Њ–≤ –≤–љ—Г—В—А–Є –Ї–ї–∞—Б—В–µ—А–∞.
–§—А–∞–Ї—В–∞–ї—М–љ–Њ–µ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–µ —В–µ—Б—В–Њ–≤—Л—Е –Њ–±—А–∞–Ј–Њ–≤.
–Р–ї–≥–Њ—А–Є—В–Љ—Л —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–≥–Њ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –Њ–±—А–∞–Ј–Њ–≤ –Њ—Б–љ–Њ–≤–∞–љ—Л –љ–∞ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є –њ–∞—А–∞–і–Є–≥–Љ—Л (—В–Њ–њ–Њ–ї–Њ–≥–Є—П —Ж–µ–ї–Є вАФ –µ—С —Д—А–∞–Ї—В–∞–ї—М–љ–∞—П —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М). –Ь–µ—В–Њ–і–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є –Њ—Б–љ–Њ–≤–Њ–є –∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤ —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–≥–Њ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П —П–≤–ї—П–µ—В—Б—П –Њ—В–Ї–∞–Ј –Њ—В —В–Њ–њ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–љ—Б—В–∞–љ—В –Є –Њ–њ–Є—Б–∞–љ–Є–µ –Ї–ї–∞—Б—Б–Њ–≤ —Ж–µ–ї–µ–є –љ–∞ —П–Ј—Л–Ї–µ –њ—А–Є–Ј–љ–∞–Ї–Њ–≤ –≤ –≤–Є–і–µ —Д—А–∞–Ї—В–∞–ї—М–љ—Л—Е —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–µ–є –Є–ї–Є —Д—А–∞–Ї—В–∞–ї—М–љ—Л—Е —Б–Є–≥–љ–∞—В—Г—А. –Р–њ—А–Є–Њ—А–љ–Њ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е –Є–ї–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ—Л—Е –њ—А–Є–Ј–љ–∞–Ї–Њ–≤ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Њ–±—Л—З–љ–Њ —Б –њ–Њ–Љ–Њ—Й—М—О –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ —В–µ—Б—В–∞. –Э–∞–Є–ї—Г—З—И–µ–Љ —В–µ—Б—В–Њ–≤—Л–Љ –Љ–∞—В–µ—А–Є–∞–ї–Њ–Љ –і–ї—П –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –Ї–Њ–љ–Ї—А–µ—В–љ—Л—Е –Ј–∞–і–∞—З —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П —П–≤–ї—П–µ—В—Б—П –љ–∞–±–Њ—А –∞–љ–∞–ї–Є–Ј–Є—А—Г–µ–Љ—Л—Е –Є —Н—В–∞–ї–Њ–љ–љ—Л—Е –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є, —А–µ–∞–ї—М–љ–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –і–∞–љ–љ–Њ–є –Ј–∞–і–∞—З–Є —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –Њ–±—К–µ–Ї—В–Њ–≤. –Ю–і–љ–∞–Ї–Њ –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В–Є –Ї–∞–ґ–і–Њ–≥–Њ –≤–Є–і–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є –≤ —А–∞–Ј–ї–Є—З–љ—Л—Е –Ј–∞–і–∞—З–∞—Е —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –Ј–∞—В—А—Г–і–љ—П—О—В –њ—А–Њ—Б–ї–µ–ґ–Є–≤–∞–љ–Є—П –Њ–±—Й–Є—Е –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В–µ–є –њ—А–Њ—Ж–µ—Б—Б–∞ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П. –Я–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –≤–Њ–њ—А–Њ—Б –Њ–± –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ–Њ–≥–Њ —В–µ—Б—В–Њ–≤–Њ–≥–Њ –Љ–∞—В–µ—А–Є–∞–ї–∞. –Т –Ї–∞—З–µ—Б—В–≤–µ —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ–Њ–≥–Њ —В–µ—Б—В–Њ–≤–Њ–≥–Њ –Љ–∞—В–µ—А–Є–∞–ї–∞ –і–ї—П –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –≤–Њ–њ—А–Њ—Б–Њ–≤ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –Њ–±—А–∞–Ј–Њ–≤ –љ–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П—Е –ї—О–±–Њ–є –њ—А–Є—А–Њ–і—Л –±—Л–ї –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ –љ–∞–±–Њ—А —Д–Є–≥—Г—А –Є–Ј (–Ґ–∞–љ–≥—А–∞–Љ–∞). –Т –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞—Е –њ—А–Є–Љ–µ–љ—П–ї–Є—Б—М 16 —Д–Є–≥—Г—А (–Ґ–∞–љ–≥—А–∞–Љ–∞) –≤–Ї–ї—О—З–∞—О—Й–Є—Е –≤ —Б–µ–±—П –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Є, —Б–Є–ї—Г—Н—В—Л –Є—Б–Ї—Г—Б—Б—В–≤–µ–љ–љ—Л—Е —Б–Њ–Њ—А—Г–ґ–µ–љ–Є–є, —Б–∞–Љ–Њ–ї–µ—В–∞, –Ї–Њ—А–∞–±–ї—П, —З–µ–ї–Њ–≤–µ–Ї–∞ –Є –ґ–Є–≤–Њ—В–љ—Л—Е.

–Т—Л—Б–Њ–Ї–∞—П —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В—М –Њ—Ж–µ–љ–Ї–Є —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є –Ї –љ–∞–ї–Є—З–Є—О –љ–µ–њ—А–µ—А—Л–≤–љ—Л—Е –Ї–Њ–љ—В—Г—А–Њ–≤ –љ–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П—Е –њ–Њ–Ј–≤–Њ–ї—П–µ—В –≥–Њ–≤–Њ—А–Є—В—М –Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є —Д–Є–ї—М—В—А–∞—Ж–Є–Є –Ї–Њ–љ—В—Г—А–Њ–≤ –Њ–±—К–µ–Ї—В–Њ–≤ –Є –Є—Е –њ–Њ–Љ–µ—Е. –° –њ–Њ–Љ–Њ—Й—М—О —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–≥–Њ –∞–ї–≥–Њ—А–Є—В–Љ–∞ —Г–і–∞–µ—В—Б—П —З–µ—В–Ї–Њ –≤—Л–і–µ–ї–Є—В—М –љ–Њ–Љ–µ—А–∞ –∞–≤—В–Њ–Љ–Њ–±–Є–ї–µ–є, –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П –Ї–Њ—В–Њ—А—Л–µ –њ–Њ–ї—Г—З–µ–љ—Л –≤ —Г—Б–ї–Њ–≤–Є—П—Е –Њ—З–µ–љ—М —Б–Є–ї—М–љ—Л—Е –њ–Њ–Љ–µ—Е (–њ—Л–ї—М, –і—Л–Љ). –Р–ї–≥–Њ—А–Є—В–Љ —Д–Є–ї—М—В—А–∞—Ж–Є–Є –Ї–Њ–љ—В—Г—А–Њ–≤ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П –Њ—Б–љ–Њ–≤–∞–љ –љ–∞ –Њ—Ж–µ–љ–Ї–µ –ї–Њ–Ї–∞–ї—М–љ–Њ–є —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є.
–Ч–∞–Ї–ї—О—З–µ–љ–Є–µ.
–Т –і–∞–љ–љ–Њ–є —А–∞–±–Њ—В–µ —Г–і–∞–ї–Њ—Б—М –Њ—В—А–∞–Ј–Є—В—М —Д—А–∞–Ї—В–∞–ї—М–љ—Г—О –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—О –Є –Ї–ї–∞—Б—В–µ—А–Є–Ј–∞—Ж–Є—О –Њ–±—К–µ–Ї—В–Њ–≤, —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є–µ —В–µ—Б—В–Њ–≤—Л—Е –Њ–±—А–∞–Ј–Њ–≤. –Т—Б–µ —Д—А–∞–Ї—В–∞–ї—М–љ—Л–µ –Љ–µ—В–Њ–і—Л –њ—А–Є–≤–Њ–і—П—В –≤ –±–Њ–ї—М—И–Є–љ—Б—В–≤–µ —Б–ї—Г—З–∞–µ–≤ –Ї –≤–µ—Б—М–Љ–∞ —Б–Є–ї—М–љ—Л–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ, –Є –Њ—В –љ–Є—Е –Љ–Њ–ґ–љ–Њ –Њ–ґ–Є–і–∞—В—М –µ—Й–µ –Њ—З–µ–љ—М –Љ–љ–Њ–≥–Њ–≥–Њ. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –Њ–±–ї–∞—Б—В–Є –њ—А–Є–Љ–µ–љ–µ–љ–Є—П —Д—А–∞–Ї—В–∞–ї—М–љ–Њ–є –Њ–±—А–∞–±–Њ—В–Ї–Є —Б–Є–≥–љ–∞–ї–Њ–≤, –њ–Њ–ї–µ–є –Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є –њ–Њ—Б—В–Њ—П–љ–љ–Њ —А–∞—Б—И–Є—А—П—О—В—Б—П. –°—В—А–µ–Љ–Є—В–µ–ї—М–љ–Њ–Љ—Г —А–∞–Ј–≤–Є—В–Є—О —Д—А–∞–Ї—В–∞–ї–Њ–≤ —Б–њ–Њ—Б–Њ–±—Б—В–≤—Г–µ—В –Є —Б–∞–Љ–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ —З—А–µ–Ј–≤—Л—З–∞–є–љ–Њ —И–Є—А–Њ–Ї–Њ–≥–Њ –Ї—А—Г–≥–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е –Є —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –њ—А–Њ–±–ї–µ–Љ, –∞–і–µ–Ї–≤–∞—В–љ–Њ –Њ–њ–Є—Б—Л–≤–∞–µ–Љ—Л—Е —Н—В–Є–Љ–Є —В–µ–Њ—А–Є—П–Љ–Є.
–°–њ–Є—Б–Њ–Ї –ї–Є—В–µ—А–∞—В—Г—А—Л.
- –Я–Њ—В–∞–њ–Њ–≤ –Р.–Р. –Э–Њ–≤–µ–є—И–Є–µ –Љ–µ—В–Њ–і—Л –Њ–±—А–∞–±–Њ—В–Ї–Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є. –Ь–Њ—Б–Ї–≤–∞ 2008.
- –Я—А–Є–≤–µ–Ј–µ–љ—Ж–µ–≤ –Ф.–У., –Ц–Є–Ј–љ—П–Ї–Њ–≤ –Р.–Ы., –С–∞—А–∞–љ–Њ–≤ –Р.–Р. –Я—А–Є–Љ–µ–љ–µ–љ–Є–µ —Д—А–∞–Ї—В–∞–ї—М–љ—Л—Е –Љ–µ—В–Њ–і–Њ–≤ –≤ –Њ–±—А–∞–±–Њ—В–Ї–µ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–є –Є —Б–Є–≥–љ–∞–ї–Њ–≤. –Ь—Г—А–Њ–Љ 2009.
- –Я–Њ—В–∞–њ–Њ–≤ –Р.–Р. –§—А–∞–Ї—В–∞–ї—Л –≤ —А–∞–і–Є–Њ—Д–Є–Ј–Є–Ї–µ –Є —А–∞–і–Є–Њ–ї–Њ–Ї–∞—Ж–Є–Є. вАФ –Ь.: –Ы–Њ–≥–Њ—Б, 2002.вАФ664 c.
- –Я–Њ—В–∞–њ–Њ–≤ –Р.–Р. –§—А–∞–Ї—В–∞–ї—М–љ—Л–µ –Љ–Њ–і–µ–ї–Є –Є –Љ–µ—В–Њ–і—Л –љ–∞ –Њ—Б–љ–Њ–≤–µ —Б–Ї–µ–є–ї–Є–љ–≥–∞ –≤ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –Є –њ—А–Є–Ї–ї–∞–і–љ—Л—Е –њ—А–Њ–±–ї–µ–Љ–∞—Е —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є —Д–Є–Ј–Є–Ї–Є. –Ь–У–Ґ–£ –Є–Љ. –Э.–≠. –С–∞—Г–Љ–∞–љ–∞, 2008. –Т—Л–њ. II. –°. 5 вАФ 107.
- –Я–Њ—В–∞–њ–Њ–≤ –Р.–Р. –§—А–∞–Ї—В–∞–ї—М–љ—Л–µ –Љ–µ—В–Њ–і—Л –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П —Д–ї—Г–Ї—В—Г–∞—Ж–Є–є —Б–Є–≥–љ–∞–ї–Њ–≤ –Є –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –і—А–Њ–±–љ–Њ–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є // –У–ї–∞–≤–∞ –≤ –Ї–љ–Є–≥–µ ¬Ђ–§–ї—Г–Ї—В—Г–∞—Ж–Є–Є –Є —И—Г–Љ—Л –≤ —Б–ї–Њ–ґ–љ—Л—Е —Б–Є—Б—В–µ–Љ–∞—Е –ґ–Є–≤–Њ–є –Є –љ–µ–ґ–Є–≤–Њ–є –њ—А–Є—А–Њ–і—Л¬ї / –Я–Њ–і —А–µ–і. –†.–Ь. –Ѓ–ї—М–Љ–µ—В—М–µ–≤–∞, –Р.–Т. –Ь–Њ–Ї—И–Є–љ–∞, –°.–Р. –Ф–µ–Љ–Є–љ–∞, –Ь.–•. –°–∞–ї–∞—Е–Њ–≤–∞.- –Ъ–∞–Ј–∞–љ—М: –Ь–Є–љ–Є—Б—В–µ—А—Б—В–≤–Њ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Є –љ–∞—Г–Ї–Є –†–µ—Б–њ—Г–±–ї–Є–Ї–Є –Ґ–∞—В–∞—А—Б—В–∞–љ, 2008.- –°. 257 вАФ 310.









